The first supervised learning method we introduce is the multinomial Naive Bayes or multinomial NB model, a probabilistic learning method. The probability of a document ![]() being in class
being in class ![]() is computed as
is computed as
where ![]() is the conditional probability of term
is the conditional probability of term ![]() occurring in a document of class
occurring in a document of class ![]() .
.![]() We interpret
We interpret ![]() as a measure of how much evidence
as a measure of how much evidence ![]() contributes that
contributes that ![]() is the correct class.
is the correct class. ![]() is the prior probability of a document occurring in class
is the prior probability of a document occurring in class ![]() . If a document's terms do not provide clear evidence for one class versus another, we choose the one that has a higher prior probability.
. If a document's terms do not provide clear evidence for one class versus another, we choose the one that has a higher prior probability. ![]() are the tokens in
are the tokens in ![]() that are part of the vocabulary we use for classification and
that are part of the vocabulary we use for classification and ![]() is the number of such tokens in
is the number of such tokens in ![]() . For example,
. For example, ![]() for the one-sentence document Beijing and Taipei join the WTO might be
for the one-sentence document Beijing and Taipei join the WTO might be ![]() , with
, with ![]() , if we treat the terms and and the as stop words.
, if we treat the terms and and the as stop words.
In text classification, our goal is to find the best class for the document. The best class in NB classification is the most likely or maximum a posteriori ( MAP ) class ![]() :
:
We write ![]() for
for ![]() because we do not know the true values of the parameters
because we do not know the true values of the parameters ![]() and
and ![]() , but estimate them from the training set as we will see in a moment.
, but estimate them from the training set as we will see in a moment.
In Equation 114, many conditional probabilities are multiplied, one for each position ![]() . This can result in a floating point underflow. It is therefore better to perform the computation by adding logarithms of probabilities instead of multiplying probabilities. The class with the highest log probability score is still the most probable;
. This can result in a floating point underflow. It is therefore better to perform the computation by adding logarithms of probabilities instead of multiplying probabilities. The class with the highest log probability score is still the most probable; ![]() and the logarithm function is monotonic. Hence, the maximization that is actually done in most implementations of NB is:
and the logarithm function is monotonic. Hence, the maximization that is actually done in most implementations of NB is:
Equation 115 has a simple interpretation. Each conditional parameter ![]() is a weight that indicates how good an indicator
is a weight that indicates how good an indicator ![]() is for
is for ![]() . Similarly, the prior
. Similarly, the prior ![]() is a weight that indicates the relative frequency of
is a weight that indicates the relative frequency of ![]() . More frequent classes are more likely to be the correct class than infrequent classes. The sum of log prior and term weights is then a measure of how much evidence there is for the document being in the class, and Equation 115 selects the class for which we have the most evidence.
. More frequent classes are more likely to be the correct class than infrequent classes. The sum of log prior and term weights is then a measure of how much evidence there is for the document being in the class, and Equation 115 selects the class for which we have the most evidence.
We will initially work with this intuitive interpretation of the multinomial NB model and defer a formal derivation to Section 13.4 .
How do we estimate the parameters ![]() and
and ![]() ? We first try the maximum likelihood estimate (MLE; probtheory), which is simply the relative frequency and corresponds to the most likely value of each parameter given the training data. For the priors this estimate is:
? We first try the maximum likelihood estimate (MLE; probtheory), which is simply the relative frequency and corresponds to the most likely value of each parameter given the training data. For the priors this estimate is:
where ![]() is the number of documents in class
is the number of documents in class ![]() and
and ![]() is the total number of documents.
is the total number of documents.
We estimate the conditional probability ![]() as the relative frequency of term
as the relative frequency of term ![]() in documents belonging to class
in documents belonging to class ![]() :
:
where ![]() is the number of occurrences of
is the number of occurrences of ![]() in training documents from class
in training documents from class ![]() , including multiple occurrences of a term in a document. We have made the positional independence assumption here, which we will discuss in more detail in the next section:
, including multiple occurrences of a term in a document. We have made the positional independence assumption here, which we will discuss in more detail in the next section: ![]() is a count of occurrences in all positions
is a count of occurrences in all positions ![]() in the documents in the training set. Thus, we do not compute different estimates for different positions and, for example, if a word occurs twice in a document, in positions
in the documents in the training set. Thus, we do not compute different estimates for different positions and, for example, if a word occurs twice in a document, in positions ![]() and
and ![]() , then
, then ![]() .
.
The problem with the MLE estimate is that it is zero for a term-class combination that did not occur in the training data. If the term WTO in the training data only occurred in China documents, then the MLE estimates for the other classes, for example UK, will be zero:
| (118) |
Now, the one-sentence document Britain is a member of the WTO will get a conditional probability of zero for UK because we are multiplying the conditional probabilities for all terms in Equation 113. Clearly, the model should assign a high probability to the UK class because the term Britain occurs. The problem is that the zero probability for WTO cannot be ``conditioned away,'' no matter how strong the evidence for the class UK from other features. The estimate is 0 because of sparseness : The training data are never large enough to represent the frequency of rare events adequately, for example, the frequency of WTO occurring in UK documents.
To eliminate zeros, we use add-one or Laplace smoothing, which simply adds one to each count (cf. Section 11.3.2 ):
where ![]() is the number of terms in the vocabulary. Add-one smoothing can be interpreted as a uniform prior (each term occurs once for each class) that is then updated as evidence from the training data comes in. Note that this is a prior probability for the occurrence of a term as opposed to the prior probability of a class which we estimate in Equation 116 on the document level.
is the number of terms in the vocabulary. Add-one smoothing can be interpreted as a uniform prior (each term occurs once for each class) that is then updated as evidence from the training data comes in. Note that this is a prior probability for the occurrence of a term as opposed to the prior probability of a class which we estimate in Equation 116 on the document level.
We have now introduced all the elements we need for training and applying an NB classifier. The complete algorithm is described in Figure 13.2 .
| docID | words in document | in |
|||
| training set | 1 | Chinese Beijing Chinese | yes | ||
| 2 | Chinese Chinese Shanghai | yes | |||
| 3 | Chinese Macao | yes | |||
| 4 | Tokyo Japan Chinese | no | |||
| test set | 5 | Chinese Chinese Chinese Tokyo Japan | ? |
Worked example. For the example in Table 13.1 , the multinomial parameters we need to classify the test document are the priors ![]() and
and ![]() and the following conditional probabilities:
and the following conditional probabilities:
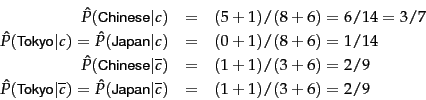
The denominators are ![]() and
and ![]() because the lengths of
because the lengths of ![]() and
and ![]() are 8 and 3, respectively, and because the constant
are 8 and 3, respectively, and because the constant ![]() in Equation 119 is 6 as the vocabulary consists of six terms.
in Equation 119 is 6 as the vocabulary consists of six terms.
We then get:
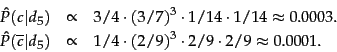
Thus, the classifier assigns the test document to ![]() = China. The reason for this classification decision is that the three occurrences of the positive indicator Chinese in
= China. The reason for this classification decision is that the three occurrences of the positive indicator Chinese in ![]() outweigh the occurrences of the two negative indicators Japan and Tokyo. End worked example.
outweigh the occurrences of the two negative indicators Japan and Tokyo. End worked example.
What is the time complexity of NB? The complexity of computing the parameters is ![]() because the set of parameters consists of
because the set of parameters consists of ![]() conditional probabilities and
conditional probabilities and ![]() priors. The preprocessing necessary for computing the parameters (extracting the vocabulary, counting terms, etc.) can be done in one pass through the training data. The time complexity of this component is therefore
priors. The preprocessing necessary for computing the parameters (extracting the vocabulary, counting terms, etc.) can be done in one pass through the training data. The time complexity of this component is therefore ![]() , where
, where ![]() is the number of documents and
is the number of documents and ![]() is the average length of a document.
is the average length of a document.
We use ![]() as a notation for
as a notation for ![]() here, where
here, where ![]() is the length of the training collection. This is nonstandard;
is the length of the training collection. This is nonstandard; ![]() is not defined for an average. We prefer expressing the time complexity in terms of
is not defined for an average. We prefer expressing the time complexity in terms of ![]() and
and ![]() because these are the primary statistics used to characterize training collections.
because these are the primary statistics used to characterize training collections.
The time complexity of APPLYMULTINOMIALNB in Figure 13.2 is ![]() .
. ![]() and
and ![]() are the numbers of tokens and types, respectively, in the test document . APPLYMULTINOMIALNB can be modified to be
are the numbers of tokens and types, respectively, in the test document . APPLYMULTINOMIALNB can be modified to be ![]() (Exercise 13.6 ). Finally, assuming that the length of test documents is bounded,
(Exercise 13.6 ). Finally, assuming that the length of test documents is bounded, ![]() because
because ![]() for a fixed constant
for a fixed constant ![]() .
.![]()
Table 13.2 summarizes the time complexities. In general, we have ![]() , so both training and testing complexity are linear in the time it takes to scan the data. Because we have to look at the data at least once, NB can be said to have optimal time complexity. Its efficiency is one reason why NB is a popular text classification method.
, so both training and testing complexity are linear in the time it takes to scan the data. Because we have to look at the data at least once, NB can be said to have optimal time complexity. Its efficiency is one reason why NB is a popular text classification method.
http://nlp.stanford.edu/IR-book/html/htmledition/naive-bayes-text-classification-1.html





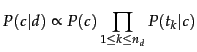
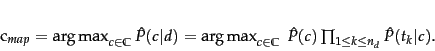
![$\displaystyle c_{map} = \argmax_{\tcjclass \in \mathbb{C}} \ [ \log \hat{P}(\tc...
...{1 \leq \tcposindex \leq n_d}
\log \hat{P}(\tcword_\tcposindex\vert\tcjclass)].$](http://nlp.stanford.edu/IR-book/html/htmledition/img882.png)
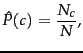
![\begin{figure}\begin{algorithm}{TrainMultinomialNB}{\mathbb{C},\docsetlabeled}
V...
...OR}\\
\RETURN{\argmax_{c \in \mathbb{C}} score[c]}
\end{algorithm}
\end{figure}](http://nlp.stanford.edu/IR-book/html/htmledition/img897.png)



相关推荐
朴素贝叶斯分类(Naive Bayes Classification)是一种基于概率理论的分类算法,因其简单而高效的特点,在机器学习领域被广泛应用。它的理论基础是贝叶斯定理,结合了特征条件独立的假设,使得计算变得相对简单。在这...
ApMl provides users with the ability to crawl the web and download pages to their computer in a directory structure suitable for a Machine Learning ... Classification Algorithms include Naive Bayes, KNN
在机器学习领域,"Naive Bayes and TAN graph model for classification" 主要涉及两种算法:朴素贝叶斯(Naive Bayes)和TAN(Tree Augmented Naive Bayes)。这两种方法常用于解决分类问题,尤其适用于文本分类、...
在自然语言处理(NLP)领域,朴素贝叶斯分类器和情感分类是两个紧密相关且广泛使用的技术。朴素贝叶斯是一种基于概率理论的简单算法,它在文本分类任务中表现出了出色的效果,尤其是在情感分析方面。...
这个压缩包"Naivebayes-classification.zip"显然包含了关于如何在Java环境下实现朴素贝叶斯分类器的相关资料,特别关注的是在处理数值型和名称型属性时的基本算法。 朴素贝叶斯算法的核心是基于贝叶斯定理,该定理...
朴素贝叶斯分类 描述 该存储库包含一些演示,这些演示在我的名... docker run -p 8888:8888 -e ENABLE_JUPYTER_LAB=YES naive-bayes 这将提示您连接到 (假设您将端口保持不变),并将对笔记本电脑和数据进行预准备。
naivebayes takes a document (piece of text), and tells you what category that document belongs to. 简单说:它可以学习文本和标签,并告诉你新的未知文本应该属于什么标签/分类。 核心公式: 文本:[W1,W2,W3,...
而贝叶斯方法,尤其是朴素贝叶斯(Naive Bayes),是处理文本分类问题的常用算法之一。这篇压缩包文件“(贝叶斯)bayes近几年的经典论文”包含了近年来在这一领域的一些高水平研究成果,为研究者提供了宝贵的资源。...
标题中的“Naive_Bayes_iris_贝叶斯检测_naive_bayes_”表明我们将探讨的是使用朴素贝叶斯算法对Iris数据集进行分类的问题。Iris数据集是一个经典的多类分类问题,而朴素贝叶斯是一种在机器学习领域广泛应用的概率...
这里我们将关注的是如何运用机器学习中的朴素贝叶斯分类算法(Naive Bayes Classification Algorithm)来解决此类问题。 朴素贝叶斯分类器是一种基于概率的分类方法,它的理论基础是贝叶斯定理。贝叶斯定理描述了在...
自然语言处理(NLP)与朴素贝叶斯分类器在文本分类中的应用是现代信息处理技术的重要组成部分。本文将深入探讨如何利用这两种技术来区分垃圾邮件(spam)和非垃圾邮件(ham)。在这个任务中,NLP用于理解和提取文本...
推文情感分析 更新(2018年9月21日):我没有积极维护该存储库。 这项工作是针对课程项目完成的,由于我不拥有版权,因此无法发布数据集。 但是,可以轻松修改此存储库中的所有内容以与其他数据集一起使用。...
naivebayes:基于muatik的naive-bayes分类器的Crystal的朴素贝叶斯分类器
本篇将深入探讨两种广泛应用于分类的算法:朴素贝叶斯(Naive Bayes)和基于朴素贝叶斯的AdaBoost增强算法。 ### 朴素贝叶斯分类器 朴素贝叶斯分类器是基于概率论的分类方法,其理论基础是贝叶斯定理。该算法假设...
| NaiveBayes.ipynb | NaiveBayes.py | ProcessDataClass.py | README.md | vectorized_url.pickle | +---data | URL Classification.csv | +---results | confusion_matrix_test.png | confusion_matrix_train.png ...
and Yu Chen and Dan Shen and Genshe Chen}, booktitle={Big Data, 2013 IEEE International Conference on}, title={Scalable Emotion Classification for Big Data analysis using Na #x00EF;ve
纲领纲领 Il programmaèstrutturato在6个档案中: main.py Documents.py 茎干 Parameter.py Training.py 分类器 Il Datasetèsuddiviso位于不同的卡特尔中: 20个新闻按日期测试 20新闻按日期列火车 ...
数据挖掘18大算法实现以及...Classification DataMining_NaiveBayes NaiveBayes-朴素贝叶斯算法 Clustering DataMining_BIRCH BIRCH-层次聚类算法 Clustering DataMining_KMeans KMeans-K均值算法 GraphMining DataMin
MNIST分类多项式vs高斯朴素贝叶斯 数据集是通过load_digits()方法从sklearn.datasets导入的。 探索数据集: 标签:0 灰色的 标签:1 单纯疱疹病毒 标签:2 X.shape()显示有1797个示例,每个示例具有64个功能。...
Master popular machine learning models including k-nearest neighbors, random forests, logistic regression, k-means, naive Bayes, and artificial neural networks Learn how to build and evaluate ...