EXTENDED LIGHTS OUT
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 6552 | Accepted: 4310 |
Description
In an extended version of the game Lights Out, is a puzzle with 5 rows of 6 buttons each (the actual puzzle has 5 rows of 5 buttons each). Each button has a light. When a button is pressed, that button and each of its (up to four) neighbors above, below, right and left, has the state of its light reversed. (If on, the light is turned off; if off, the light is turned on.) Buttons in the corners change the state of 3 buttons; buttons on an edge change the state of 4 buttons and other buttons change the state of 5. For example, if the buttons marked X on the left below were to be pressed,the display would change to the image on the right.
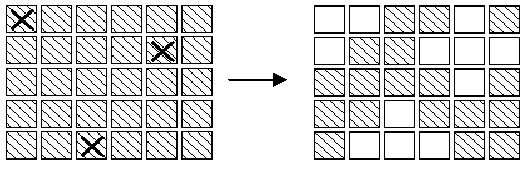
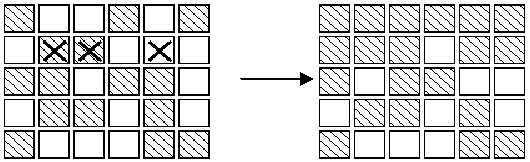
The aim of the game is, starting from any initial set of lights on in the display, to press buttons to get the display to a state where all lights are off. When adjacent buttons are pressed, the action of one button can undo the effect of another. For instance, in the display below, pressing buttons marked X in the left display results in the right display.Note that the buttons in row 2 column 3 and row 2 column 5 both change the state of the button in row 2 column 4,so that, in the end, its state is unchanged.
Note:
1. It does not matter what order the buttons are pressed.
2. If a button is pressed a second time, it exactly cancels the effect of the first press, so no button ever need be pressed more than once.
3. As illustrated in the second diagram, all the lights in the first row may be turned off, by pressing the corresponding buttons in the second row. By repeating this process in each row, all the lights in the first
four rows may be turned out. Similarly, by pressing buttons in columns 2, 3 ?, all lights in the first 5 columns may be turned off.
Write a program to solve the puzzle.

The aim of the game is, starting from any initial set of lights on in the display, to press buttons to get the display to a state where all lights are off. When adjacent buttons are pressed, the action of one button can undo the effect of another. For instance, in the display below, pressing buttons marked X in the left display results in the right display.Note that the buttons in row 2 column 3 and row 2 column 5 both change the state of the button in row 2 column 4,so that, in the end, its state is unchanged.

Note:
1. It does not matter what order the buttons are pressed.
2. If a button is pressed a second time, it exactly cancels the effect of the first press, so no button ever need be pressed more than once.
3. As illustrated in the second diagram, all the lights in the first row may be turned off, by pressing the corresponding buttons in the second row. By repeating this process in each row, all the lights in the first
four rows may be turned out. Similarly, by pressing buttons in columns 2, 3 ?, all lights in the first 5 columns may be turned off.
Write a program to solve the puzzle.
Input
The first line of the input is a positive integer n which is the number of puzzles that follow. Each puzzle will be five lines, each of which has six 0 or 1 separated by one or more spaces. A 0 indicates that the light is off, while a 1 indicates that the light is on initially.
Output
For each puzzle, the output consists of a line with the string: "PUZZLE #m", where m is the index of the puzzle in the input file. Following that line, is a puzzle-like display (in the same format as the input) . In this case, 1's indicate buttons that must be pressed to solve the puzzle, while 0 indicate buttons, which are not pressed. There should be exactly one space between each 0 or 1 in the output puzzle-like display.
Sample Input
2 0 1 1 0 1 0 1 0 0 1 1 1 0 0 1 0 0 1 1 0 0 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 1 0 0 0 1 0 1 0 0
Sample Output
PUZZLE #1 1 0 1 0 0 1 1 1 0 1 0 1 0 0 1 0 1 1 1 0 0 1 0 0 0 1 0 0 0 0 PUZZLE #2 1 0 0 1 1 1 1 1 0 0 0 0 0 0 0 1 0 0 1 1 0 1 0 1 1 0 1 1 0 1
题意:
给出 T 组样例,后给出一个 5 X 6 的矩阵,0 代表灯关,1 代表灯亮,每按一个键本身的灯和周围的四个相邻位置的灯也会改变状态,每组输出一个矩阵,该矩阵表示按或者不按的情况,1 代表按,0 代表不按,问要如何按灯使最终所有的灯都变成是关闭状态,即都变成 0。
思路:
高斯消元。要把所有的灯都变成 0,也可以反过来看,当所有灯为 0 的时候转变为所要求的灯的情况。
列成 30 个 30 元 1 次方程,即每个灯的 0,1 情况用 a,b,c,d……表示,每按一个键都会有不同的状态,故把 30 种子状态(子矩阵)表示出来,将给出 30 个灯的状态转变为方程的右等式。后运用高斯消元求出答案即可。消元过程要运用到异或,因为只有 0,1 两种状态,异或 0,代表不改变当前灯的状况,异或 1 代表要该表当前灯的状态。
详细过程:http://blog.csdn.net/u013081425/article/details/24452153
AC:
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef vector<int> vec;
typedef vector<vec> mat;
mat res(30, vec(31));
void gauss_jordan() {
for (int i = 0; i < 30; ++i) {
int pivot = i;
for (; pivot < 30; ++pivot)
if (res[pivot][i]) break;
swap(res[i], res[pivot]);
for (int j = 0; j < 30; ++j) {
if (i != j && res[j][i]) {
for (int k = 0; k <= 30; ++k) {
res[j][k] = res[i][k] ^ res[j][k];
}
}
}
}
}
int main() {
int t;
scanf("%d", &t);
for (int tt = 1; tt <= t; ++tt) {
for (int i = 0; i < 5; ++i) {
for (int j = 0; j < 6; ++j) {
int ans = i * 6 + j;
scanf("%d", &res[ans][30]);
res[ans][ans] = 1;
if (j - 1 >= 0) res[ans][ans - 1] = 1;
if (i - 1 >= 0) res[ans][ans - 6] = 1;
if (j + 1 < 6) res[ans][ans + 1] = 1;
if (i + 1 < 5) res[ans][ans + 6] = 1;
}
}
gauss_jordan();
printf("PUZZLE #%d\n", tt);
for (int i = 0; i < 5; ++i) {
for (int j = 0; j < 6; ++j) {
int ans = i * 6 + j;
printf("%d", res[ans][30]);
j == 5 ? printf("\n") : printf(" ");
}
}
}
return 0;
}








相关推荐
WPF Toolkit Extended是一款针对Windows Presentation Foundation(WPF)框架的扩展工具包,它为开发者提供了丰富的控件和功能,以增强WPF应用程序的用户体验和开发效率。最新版本的WPF Toolkit Extended兼容.NET ...
Acrobat 9.3 Pro Extended x86 简体中文语言包 (MJY) part3 上传容量限制分5个rar压缩包,这是part3 Acrobat 9.3 Pro Extended x86 简体中文语言包(MJY) 适用于x86操作系统,请先安装Acrobat 9 Pro Extended英文...
### Oracle RAC on Extended Distance (Stretched) Clusters #### 什么是Extended Distance Oracle RAC集群? Extended Distance Oracle RAC(也称为Stretched Cluster)是一种特殊配置的Oracle Real Application ...
在此背景下,由耶鲁大学研究人员创建的“extended YaleB人脸库”成为了研究人脸识别技术的重要工具,特别是在光照变化影响下的人脸识别研究领域。 “extended YaleB人脸库”是一个包含了丰富数据的数据库,其旨在...
**WPF Extended.Wpf.Toolkit加载界面Demo** WPF(Windows Presentation Foundation)是.NET框架的一部分,用于构建具有丰富图形、多媒体和数据绑定功能的桌面应用程序。在开发WPF应用时,我们常常需要为用户提供一...
"前端开源库-extended"就是一个专为前端开发者设计的开源库,其主要目标是帮助开发者更有效地管理和整合多个库,从而创建一个统一、高效的工作环境。这个库被称为"extended",它通过扩展其他库的功能,实现对多个库...
为了帮助用户更有效地管理挂机过程,"Idle Master Extended v1.5 idlemaster"应运而生。这款应用程序是专门为那些想要快速挂机游戏,尤其是那些需要长时间运行才能解锁内容的游戏设计的。 首先,我们来理解一下...
Adobe Acrobat 9 Pro Extended Patcher and KeyGen
Adobe Acrobat.9 Pro Extended MULTILANGUAGE FINAL ISO
《Yale和Extended Yale B人脸数据库:深度学习与计算机视觉中的关键资源》 在计算机视觉领域,人脸识别是一项至关重要的任务,它涉及到大量的数据集来训练和验证算法。Yale和Extended Yale B人脸数据库就是这样的两...
Extended Yale B Database,The cropped Extended Yale B database consists of 2414 frontal-face images of 38 subjects with size 168×192, captured under 64 different lighting conditions. EYaleB是耶鲁...
**WPF Toolkit Extended** 是一个基于Windows Presentation Foundation (WPF) 的开源库,它扩展了Microsoft官方的WPF Toolkit,提供了更多丰富的控件和功能。这个库不仅包含了完整的源代码,便于开发者深入理解和...
Oracle Extended RAC,全称为Real Application Clusters (RAC) Extended Data Guard,是Oracle数据库11g版本中引入的一种高级集群技术,旨在提供高可用性和灾难恢复能力。它扩展了传统的RAC功能,允许数据库在两个...
Adobe Acrobat 9.0 Pro Extended 是一款由Adobe公司推出的高级PDF文档处理软件,它在标准版的基础上增加了更多专业和高级功能。Keymaker是指一个程序,通常用于生成软件的激活码或序列号,使得用户能够在未购买的...
【jenkins】Extended Choice Parameter参数选择插件,方便自动化控制流程使用,根据预选的参数选择对应的自动化流程。
Extended WPF Toolkit是一款针对Windows Presentation Foundation (WPF) 应用程序开发的开源工具集,其版本3.0.0提供了丰富的控件和功能,帮助开发者扩展WPF平台的原生功能,提升用户体验和应用程序的交互性。...
《前端开源库-is-extended:深入理解类型检测的利器》 在现代前端开发中,类型检测是必不可少的一个环节。为了确保代码的健壮性和可维护性,开发者需要精确地识别和处理不同类型的变量。"is-extended"是一个专门...
Adobe Acrobat 9 Pro Extended是一款强大的PDF处理软件,它在Adobe Acrobat 9的基础上增加了更多专业级的功能,如3D文档创建、编辑和查看。本官方教程是针对英文用户编写的,全面覆盖了Acrobat 9 Pro Extended的各项...
Acrobat 9.3 Pro Extended x86 简体中文语言包 (MJY) part4 上传容量限制分5个rar压缩包,这是part4 Acrobat 9.3 Pro Extended x86 简体中文语言包(MJY) 适用于x86操作系统,请先安装Acrobat 9 Pro Extended英文...
KF的假设之一就是高斯分布的xx预测后仍服从高斯分布,高斯分布的xx变换到测量空间后仍服从高斯分布。可是,假如F、H是非线性变换,那么上述条件则不成立,详细见我的博客...