H.O.T. 指更高阶,在移动足够小的情况下可以忽略。从这个方程中我们可以得到:
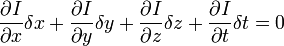
或者
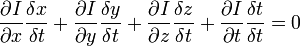
我们得到:

Vx,Vy,Vz 分别是I(x,y,z,t)的光流向量中x,y,z的组成。 ,
,
 ,
,
 和
和
 则是图像在
(x,y,z,t)这一点向相应方向的差分。
则是图像在
(x,y,z,t)这一点向相应方向的差分。
所以
IxVx + IyVy + IzVz = − It。
写做:

这个方程有三个未知量,尚不能被解决,这也就是所谓光流算法的光圈问题。那么要找到光流向量则需要另一套解决的方案。而Lucas-Kanade算法是一个非迭代的算法:
假设流(Vx,Vy,Vz)在一个大小为m*m*m(m>1)的小窗中是一个常数,那么从像素1...n, n = m3中可以得到下列一组方程:



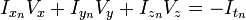
三个未知数但是有多于三个的方程,这个方程组自然是个超定方程,也就是说方程组内有冗余,方程组可以表示为:
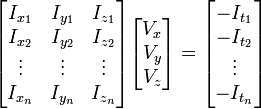
记作:
为了解决这个超定问题,我们采用最小二乘法:
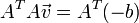 or
or
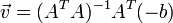
得到:
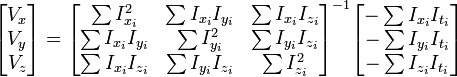
其中的求和是从1到n。
这也就是说寻找光流可以通过在四维上图像导数的分别累加得出。我们还需要一个权重函数W(i, j,k), ![i,j,k \in [1,m]](http://upload.wikimedia.org/math/a/c/e/acee99b6db15dea65d0984f2d95429f3.png) 来突出窗口中心点的坐标。高斯函数做这项工作是非常合适的,
来突出窗口中心点的坐标。高斯函数做这项工作是非常合适的,
这个算法的不足在于它不能产生一个密度很高的流向量,例如在运动的边缘和黑大的同质区域中的微小移动方面流信息会很快的褪去。它的优点在于有噪声存在的鲁棒性还是可以的。
补充:opencv里实现的看上去蛮复杂,现在还不是太明白。其中LK经典算法也是迭代法,是由高斯迭代法解线性方程组进行迭代的。
参考文献:Lucas B and Kanade T. An Iterative Image Registration Technique with an Application to Stereo Vision. Proc. Of 7th International Joint Conference on Artificial Intelligence (IJCAI), pp.674-679.是81年发表的。
opencv中实现的是84年发表的算法,
参考文献:Bruce D. Lucas, "Generalized Image Matching by the Method of Differences," doctoral dissertation, tech. report , Robotics Institute, Carnegie Mellon University, July, 1984
这篇论文是收费的,一直都没下到还。
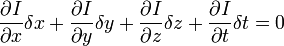
或者
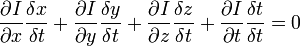
我们得到:

Vx,Vy,Vz 分别是I(x,y,z,t)的光流向量中x,y,z的组成。
 ,
,
 ,
,
 和
和
 则是图像在
(x,y,z,t)这一点向相应方向的差分。
则是图像在
(x,y,z,t)这一点向相应方向的差分。
所以




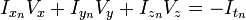
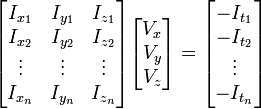

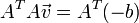 or
or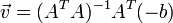
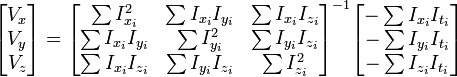
![i,j,k \in [1,m]](http://upload.wikimedia.org/math/a/c/e/acee99b6db15dea65d0984f2d95429f3.png) 来突出窗口中心点的坐标。高斯函数做这项工作是非常合适的,
来突出窗口中心点的坐标。高斯函数做这项工作是非常合适的,


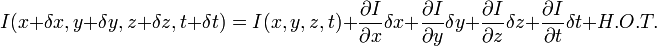



相关推荐
算法实现了Lucas_Kanade光流场算法,得到平滑的运动矢量
Lucas-Kanade 算法是一种常用的光流估计方法,但其存在一些缺点,例如在图像纹理欠丰富区域的光流估计结果较差。本文提出了一种改进的 Lucas-Kanade 光流估计方法,该方法定义了新的跟踪置信度因子,消除权值对光流...
本篇文章将深入探讨Lucas-Kanade光流算法的原理、实现方式以及在MATLAB环境下的应用。 首先,光流的基本概念是基于物理假设:相邻帧间的亮度恒定。它试图找出图像中每个像素在连续帧间的位置变化,即像素的运动矢量...
Lucas-Kanade方法是光流算法的一种经典实现,由Lucas和Kanade在1981年提出。 在Lucas-Kanade光流法中,关键步骤包括: 1. **特征检测**:首先,需要在连续的两帧图像中检测出稳定的特征点。这些点通常具有显著的...
2.领域:三维Lucas-Kanade光流提取算法。 3.内容:基于matlab的三维Lucas-Kanade光流提取算法仿真。 x=ux(1:f:size(ux,1),1:f:size(ux,2),1:f:size(ux,3)); y=uy(1:f:size(ux,1),1:f:size(ux,2),1:f:size(ux,3)); ...
Lucas-Kanade光流法是计算机视觉领域中一种经典的图像运动分析算法,主要用于估计图像序列中像素在时间上的连续移动。它由Bruce Lucas和Takeo Kanade在1981年提出,因其简单而有效的特性,被广泛应用于视频处理、...
总的来说,Lucas-Kanade光流估计算法是计算机视觉中一种高效且实用的方法,它通过局部灰度不变性假设来估计像素的运动,是理解图像序列动态的关键工具。这个压缩包提供的资源可以帮助读者深入了解并实现这一算法。
在本压缩包中提供的Matlab代码,是针对3D图像进行Lucas-Kanade光流法的实现。对于初学者或是需要进行相关研究的人员来说,这份代码提供了极大的便利,因为它不仅包含了基本的算法实现,而且还附带了参数化编程的特性...
2.领域:智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,更多内容可点击博主头像 3.内容:标题所示,对于介绍可点击主页搜索博客 4.适合人群:本科,硕士...
Lucas-Kanade方法是一种经典光流算法,主要用于计算图像序列中像素点的运动。它通过最小化目标函数来求解光流场,通常用于动态场景分析、视频跟踪、动作捕捉等领域。结合金字塔法和Lucas-Kanade算法,本代码能够更好...
2.内容:对视频目标进行光流提取,对比Lucas-Kanade和Horn-Schunck+matlab操作视频 3.用处:用于Lucas-Kanade和Horn-Schunck算法编程学习 4.指向人群:本硕博等教研学习使用 5.运行注意事项: 使用matlab2021a...
总之,Lucas-Kanade光流估算是图像处理领域的一个基础而重要的技术,它利用MATLAB的便利性提供了直观的实现方式。掌握这种算法对于理解和应用计算机视觉技术至关重要,特别是在实时视频分析、自动驾驶、无人机导航等...
Lucas-Kanade(LK)光流法是最早且最著名的光流算法之一,由Bruce Lucas和Takeo Kanade于1981年提出。这个算法基于小波运动假设,即邻近像素共享相同的运动。在本项目中,我们将深入探讨如何使用MATLAB来实现迭代...
《Lucas-Kanade光流算法在MATLAB中的实现》 光流是计算机视觉领域中的一个核心概念,它描述了图像序列中像素的运动轨迹。Lucas-Kanade(L-K)光流法是由Bruce Lucas和Takeo Kanade在1981年提出的,是一种基于像素级...
总的来说,Lucas-Kanade光流法是计算机视觉中的经典算法,它的理论基础和实现细节对于理解图像运动分析至关重要。通过提供的代码,我们可以更深入地了解光流法的工作原理,并将其应用于实际项目中。
在提供的文件名`www.pudn.com.txt`和`lk20_p2_release`中,`www.pudn.com.txt`可能是相关资料的链接,而`lk20_p2_release`可能是一个MATLAB代码文件或程序包,用于实现Lucas-Kanade光流算法。你可以通过阅读这个文件...
光流算法的实现实现有4个部分: 朴素密集光流。 ( opticalFlow.m ) 最小特征值的opticalFlow.m和阈值是自由参数基于角点的稀疏光流角点检测基于高斯偏差( CornerDetect.m , gaussian.m , d_gaussian.m ) 迭代粗到...
光流算法的假设条件是亮度恒定,就是同一点随着时间的变化,其亮度不会发生改变,用于得到光流法基本方程;基于opencv实现,可实现最小障碍检测光流算法。