改进前序遍历树—–关于无限分类的问题

 

现在，让我们看另一种存储树的方法。递归可能会很慢，所以我们就尽量不使用递归函数。我们也想尽量减少数据库查询的次数。最好是每次只需要查询一次。

我们先把树按照水平方式摆开。从根节点开始（“Food”），然后他的左边写上1。然后按照树的顺序（从上到下）给“Fruit”的左边写上2。这 样，你沿着树的边界走啊走（这就是“遍历”），然后同时在每个节点的左边和右边写上数字。最后，我们回到了根节点“Food”在右边写上18。下面是标上 了数字的树，同时把遍历的顺序用箭头标出来了。

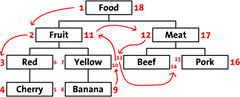
我们称这些数字为左值和右值（如，“Food”的左值是1，右值是18）。正如你所见，这些数字按时了每个节点之间的关系。因为“Red”有3和6 两个值，所以，它是有拥有1-18值的“Food”节点的后续。同样的，我们可以推断所有左值大于2并且右值小于11的节点，都是有2-11的 “Food”节点的后续。这样，树的结构就通过左值和右值储存下来了。这种数遍整棵树算节点的方法叫做“改进前序遍历树”算法。

在继续前，我们先看看我们的表格里的这些值：

注意单词“left”和“right”在SQL中有特殊的含义。因此，我们只能用“lft”和“rgt”来表示这两个列。（译注——其实Mysql 中可以用“`”来表示，如“`left`”，MSSQL中可以用“[]”括出，如“[left]”，这样就不会和关键词冲突了。）同样注意这里我们已经不 需要“parent”列了。我们只需要使用lft和rgt就可以存储树的结构。

获取树

如果你要通过左值和右值来显示这个树的话，你要首先标识出你要获取的那些节点。例如，如果你想获得“Fruit”子树，你要选择那些左值在2到11的节点。用SQL语句表达：

SELECT * FROM tree WHERE lft BETWEEN 2 AND 11;

这个会返回：

好吧，现在整个树都在一个查询中了。现在就要像前面的递归函数那样显示这个树，我们要加入一个ORDER BY子句在这个查询中。如果你从表中添加和删除行，你的表可能就顺序不对了，我们因此需要按照他们的左值来进行排序。

SELECT * FROM tree WHERE lft BETWEEN 2 AND 11 ORDER BY lft ASC;

就只剩下缩进的问题了。

要显示树状结构，子节点应该比他们的父节点稍微缩进一些。我们可以通过保存一个右值的一个栈。每次你从一个节点的子节点开始时，你把这个节点的右值 添加到栈中。你也知道子节点的右值都比父节点的右值小，这样通过比较当前节点和栈中的前一个节点的右值，你可以判断你是不是在显示这个父节点的子节点。当 你显示完这个节点，你就要把他的右值从栈中删除。要获得当前节点的层数，只要数一下栈中的元素。

<?php
function display_tree($root) {
    // 获得$root节点的左边和右边的值
    $result = mysql_query('SELECT lft, rgt FROM tree '.
                           'WHERE title="'.$root.'";');
    $row = mysql_fetch_array($result); 

    // 以一个空的$right栈开始
    $right = array(); 

    // 现在，获得$root节点的所有后序
    $result = mysql_query('SELECT title, lft, rgt FROM tree '. 

      'WHERE lft BETWEEN '.$row['lft'].' AND '.
                           $row['rgt'].' ORDER BY lft ASC;'); 

    // 显示每一行
  while ($row = mysql_fetch_array($result)) {
    // 检查栈里面有没有元素
    if (count($right)>0) {
      // 检查我们是否需要从栈中删除一个节点
      while ($right[count($right)-1]<$row['rgt']) {
        array_pop($right);
      }
    } 

    // 显示缩进的节点标题
    echo str_repeat('  ',count($right)).$row['title']."\n"; 

    // 把这个节点添加到栈中
    $right[] = $row['rgt'];
  }
  }
  ?>

如果运行这段代码，你可以获得和上一部分讨论的递归函数一样的结果。而这个函数可能会更快一点：他不采用递归而且只是用了两个查询

节点的路径

有了新的算法，我们还要另找一种新的方法来获得指定节点的路径。这样，我们就需要这个节点的祖先的一个列表。

由于新的表结构，这不需要花太多功夫。你可以看一下，例如，4-5的“Cherry”节点，你会发现祖先的左值都小于4，同时右值都大于5。这样，我们就可以使用下面这个查询：

SELECT title FROM tree WHERE lft < 4 AND rgt > 5 ORDER BY lft ASC;

注意，就像前面的查询一样，我们必须使用一个ORDER BY子句来对节点排序。这个查询将返回：

+-------+
| title |
+-------+
| Food  |
| Fruit |
| Red   |
+-------+

我们现在只要把各行连起来，就可以得到“Cherry”的路径了。

有多少个后续节点？How Many Descendants

如果你给我一个节点的左值和右值，我就可以告诉你他有多少个后续节点，只要利用一点点数学知识。

因为每个后续节点依次会对这个节点的右值增加2，所以后续节点的数量可以这样计算：

descendants = (right – left - 1) / 2

利用这个简单的公式，我可以立刻告诉你2-11的“Fruit”节点有4个后续节点，8-9的“Banana”节点只是1个子节点，而不是父节点。

自动化树遍历

现在你对这个表做一些事情，我们应该学习如何自动的建立表了。这是一个不错的练习，首先用一个小的树，我们也需要一个脚本来帮我们完成对节点的计数。

让我们先写一个脚本用来把一个邻接列表转换成前序遍历树表格。

<?php
function rebuild_tree($parent, $left) {
    // 这个节点的右值是左值加1
    $right = $left+1; 

    // 获得这个节点的所有子节点
    $result = mysql_query('SELECT title FROM tree '.
                           'WHERE parent="'.$parent.'";');
    while ($row = mysql_fetch_array($result)) {
        // 对当前节点的每个子节点递归执行这个函数
        // $right 是当前的右值，它会被rebuild_tree函数增加
        $right = rebuild_tree($row['title'], $right);
    } 

    // 我们得到了左值，同时现在我们已经处理这个节点我们知道右值的子节点
    mysql_query('UPDATE tree SET lft='.$left.', rgt='.
                 $right.' WHERE title="'.$parent.'";'); 

    // 返回该节点的右值+1
    return $right+1;
}
?>

这是一个递归函数。你要从rebuild_tree('Food',1); 开始，这个函数就会获取所有的“Food”节点的子节点。

如果没有子节点，他就直接设置它的左值和右值。左值已经给出了，1，右值则是左值加1。如果有子节点，函数重复并且返回最后一个右值。这个右值用来作为“Food”的右值。

递归让这个函数有点复杂难于理解。然而，这个函数确实得到了同样的结果。他沿着树走，添加每一个他看见的节点。你运行了这个函数之后，你会发现左值和右值和预期的是一样的（一个快速检验的方法：根节点的右值应该是节点数量的两倍）。

添加一个节点

我们如何给这棵树添加一个节点？有两种方式：在表中保留“parent”列并且重新运行rebuild_tree()
函数——一个很简单但却不是很优雅的函数；或者你可以更新所有新节点右边的节点的左值和右值。

第一个想法比较简单。你使用邻接列表方法来更新，同时使用改进前序遍历树来查询。如果你想添加一个新的节点，你只需要把节点插入表格，并且设置好parent列。然后，你只需要重新运行rebuild_tree() 函数。这做起来很简单，但是对大的树效率不高。

第二种添加和删除节点的方法是更新新节点右边的所有节点。让我们看一下例子。我们要添加一种新的水果——“Strawberry”，作为“Red” 的最后一个子节点。首先，我们要腾出一个空间。“Red”的右值要从6变成8，7-10的“Yellow”节点要变成9-12，如此类推。更新“Red” 节点意味着我们要把所有左值和右值大于5的节点加上2。

我们用一下查询：

UPDATE tree SET rgt=rgt+2 WHERE rgt>5;
UPDATE tree SET lft=lft+2 WHERE lft>5;

现在我们可以添加一个新的节点“Strawberry”来填补这个新的空间。这个节点左值为6右值为7。

INSERT INTO tree SET lft=6, rgt=7, title='Strawberry';

如果我们运行display_tree() 函数，我们将发现我们新的“Strawberry”节点已经成功地插入了树中：

Food
  Fruit
    Red
      Cherry
      Strawberry
    Yellow
      Banana
  Meat
    Beef
    Pork

缺点

首先，改进前序遍历树算法看上去很难理解。它当然没有邻接列表方法简单。然而，一旦你习惯了左值和右值这两个属性，他就会变得清晰起来，你可以用这 个技术来完成临街列表能完成的所有事情，同时改进前序遍历树算法更快。当然，更新树需要很多查询，要慢一点，但是取得节点却可以只用一个查询。

评论

1 楼 fangguojun 2010-08-16  

在插入新记录是提到的把所有左值和右值大于5的节点加上2，这里的5是如何得来的，是父节点的右值减1吗？