<!-- Search Google -->
 输入您的搜索字词 提交搜索表单 输入您的搜索字词 提交搜索表单
|
<!-- Search Google -->
在平面解析几何中,圆的方程可以描述为(x – x0)2 + (y – y0)2 = R2,其中(x0, y0)是圆心坐标,R是圆的半径,特别的,当(x0, y0)就是坐标中心点时,圆方程可以简化为x2 + y2 = R2。在计算机图形学中,圆和直线一样,也存在在点阵输出设备上显示或输出的问题,因此也需要一套光栅扫描转换算法。为了简化,我们先考虑圆心在原点的圆的生成,对于中心不是原点的圆,可以通过坐标的平移变换获得相应位置的圆。
在进行扫描转换之前,需要了解一个圆的特性,就是圆的八分对成性。如图(1)所示:
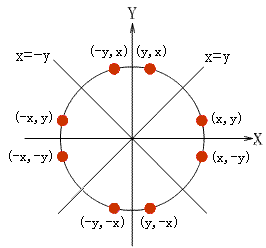
图(1)圆的八分对称性
圆心位于原点的圆有四条对称轴x = 0、y = 0、x = y和x = -y,若已知圆弧上一点P(x,y),就可以得到其关于四条对称轴的七个对称点:(x, -y)、(-x, y)、(-x, -y)、(y, x)、(y, -x)、(-y, x)、(-y, -x),这种性质称为八分对称性。因此只要能画出八分之一的圆弧,就可以利用对称性的原理得到整个圆。
有几种较容易的方法可以得到圆的扫描转换,首先介绍一下直角坐标法。已知圆方程:x2 + y2 = R2,若取x作为自变量,解出y,得到:
y =
在生成圆时先扫描转换四分之一的圆周,让自变量x从0到R以单位步长增加,在每一步时可解出y,然后调用画点函数即可逐点画出圆。但这样做,由于有乘方和平方根运算,并且都是浮点运算,算法效率不高。而且当x接近R值时(圆心在原点),在圆周上的点(R,0)附近,由于圆的斜率趋于无穷大,因浮点数取整需要四舍五入的缘故,使得圆周上有较大的间隙。接下来介绍一下极坐标法,假设直角坐标系上圆弧上一点P(x,y)与x轴的夹角是θ,则圆的极坐标方程为:
x = Rcosθ
y = Rsinθ
生成圆是利用圆的八分对称性,使自变量θ的取值范围为(0,45°)就可以画出整圆。这个方法涉及三角函数计算和乘法运算,计算量较大。直角坐标法和极坐标法都是效率不高的算法,因此只是作为理论方法存在,在计算机图形学中基本不使用这两种方法生成圆。下面就介绍几种在计算机图形学中比较实用的圆的生成算法。
1、 中点画圆法
首先是中点画圆法,考虑圆心在原点,半径为R的圆在第一象限内的八分之一圆弧,从点(0, R)到点(R/ , R/ )顺时针方向确定这段圆弧。假定某点Pi(xi, yi)已经是该圆弧上最接近实际圆弧的点,那么Pi的下一个点只可能是正右方的P1或右下方的P2两者之一,如图(2)所示:
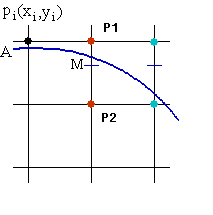
图(2)中点划线法示例
构造判别函数:
F(x, y)= x2 + y2 – R2
当F(x, y)= 0,表示点在圆上,当F(x, y)> 0,表示点在圆外,当F(x, y)< 0,表示点在圆内。如果M是P1和P2的中点,则M的坐标是(xi + 1, yi – 0.5),当F(xi + 1, yi – 0.5)< 0时,M点在圆内,说明P1点离实际圆弧更近,应该取P1作为圆的下一个点。同理分析,当F(xi + 1, yi – 0.5)> 0时,P2离实际圆弧更近,应取P2作为下一个点。当F(xi + 1, yi – 0.5)= 0时,P1和P2都可以作为圆的下一个点,算法约定取P2作为下一个点。
现在将M点坐标(xi + 1, yi – 0.5)带入判别函数F(x, y),得到判别式d:
d = F(xi + 1, yi – 0.5)= (xi + 1)2 + (yi – 0.5)2 – R2
若d < 0,则取P1为下一个点,此时P1的下一个点的判别式为:
d’ = F(xi + 2, yi – 0.5)= (xi + 2)2 + (yi – 0.5)2 – R2
展开后将d带入可得到判别式的递推关系:
d’ = d + 2xi + 3
若d > 0,则取P2为下一个点,此时P2的下一个点的判别式为:
d’ = F(xi + 2, yi – 1.5)= (xi + 2)2 + (yi – 1.5)2 – R2
展开后将d带入可得到判别式的递推关系:
d’ = d + 2(xi - yi) + 5
特别的,在第一个象限的第一个点(0, R)时,可以推倒出判别式d的初始值d0:
d0 = F(1, R – 0.5) = 1 – (R – 0.5)2 – R2 = 1.25 - R
根据上面的分析,可以写出中点画圆法的算法。考虑到圆心不在原点的情况,需要对计算出来的坐标进行了平移,下面就是通用的中点画圆法的源代码:
26void MP_Circle(int xc , int yc , int r)
27{
28 int x, y;
29 double d;
30
31 x = 0;
32 y = r;
33 d = 1.25 - r;
34 CirclePlot(xc , yc , x , y);
35 while(x < y)
36 {
37 if(d < 0)
38 {
39 d = d + 2 * x + 3;
40 }
41 else
42 {
43 d = d + 2 * ( x - y ) + 5;
44 y--;
45 }
46 x++;
47 CirclePlot(xc , yc , x , y);
48 }
49}
|
参数xc和yc是圆心坐标,r是半径,CirclePlot()函数是参照圆的八分对称性完成八个点的位置计算的辅助函数。
2、 改进的中点画圆法-Bresenham算法
中点画圆法中,计算判别式d使用了浮点运算,影响了圆的生成效率。如果能将判别式规约到整数运算,则可以简化计算,提高效率。于是人们针对中点画圆法进行了多种改进,其中一种方式是将d的初始值由1.25 – R改成1 – R,考虑到圆的半径R总是大于2,因此这个修改不会响d的初始值的符号,同时可以避免浮点运算。还有一种方法是将d的计算放大两倍,同时将初始值改成3 – 2R,这样避免了浮点运算,乘二运算也可以用移位快速代替,采用3 – 2R为初始值的改进算法,又称为Bresenham算法:
52void Bresenham_Circle(int xc , int yc , int r)
53{
54 int x, y, d;
55
56 x = 0;
57 y = r;
58 d = 3 - 2 * r;
59 CirclePlot(xc , yc , x , y);
60 while(x < y)
61 {
62 if(d < 0)
63 {
64 d = d + 4 * x + 6;
65 }
66 else
67 {
68 d = d + 4 * ( x - y ) + 10;
69 y--;
70 }
71 x++;
72 CirclePlot(xc , yc , x , y);
73 }
74}
|
3、 正负判定画圆法
除了中点画圆算法,还有一种画圆算法也是利用当前点产生的圆函数进行符号判别,利用负反馈调整以决定下一个点的产生来直接生成圆弧,就是正负法,下面就介绍一下正负法的算法实现。
正负法根据圆函数:F(x, y)= x2 + y2 – R2的值,将平面区域分成圆内和圆外,如图(3)所示:
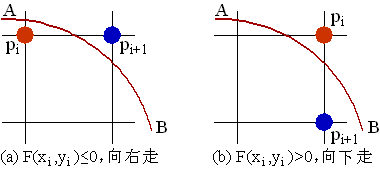
图(3)正负法判定示意图
假设圆弧的生成方向是从A到B方向,当某个点Pi被确定以后,Pi的下一个点Pi+1的取值就根据F(xi, yi)的值进行判定,判定的原则是:
1、当F(xi, yi)≤ 0时:取xi+1 = xi+1,yi+1 = yi。即向右走一步,从圆内走向圆外。对应图(3-a)中的从Pi到Pi+1。
2、当F(xi, yi)> 0时:取xi+1 = xi,yi+1 = yi - 1。即向下走一步,从圆外走向圆内。对应图(3-b)中的从Pi到Pi+1。
由于下一个点的取向到底是向圆内走还是向圆外走取决于F(xi, yi)的正负,因此称为正负法。对于判别式F(xi, yi)的递推公式,也要分两种情况分别推算:
1、当F(xi, yi)≤ 0时,Pi的下一个点Pi+1取xi+1 = xi+1,yi+1 = yi,判别式F(xi+1, yi+1)的推算过程是:
F(xi+1, yi+1)= F(xi+1,yi) = (xi+1)2+yi2-R2 = (xi2+yi2-R2)+2xi+1 = F(xi,yi)+2xi+1
2、当F(xi, yi)> 0时,Pi的下一个点Pi+1取xi+1 = xi,yi+1 = yi - 1,判别式F(xi+1, yi+1)的推算过程是:
F(xi+1, yi+1)= F(xi,yi-1) = xi2+(yi-1)2 - R2 = (xi2+yi2-R2) - 2yi + 1 = F(xi,yi) - 2yi+1
设画圆的初始点是(0,R),判定式的初始值是0,正负法生成圆的算法如下:
105void Pnar_Circle(int xc, int yc, int r)
106{
107 int x, y, f;
108
109 x = 0;
110 y = r;
111 f = 0;
112 while(x <= y)
113 {
114 CirclePlot(xc, yc, x, y);
115 if(f <= 0)
116 {
117 f = f + 2 * x + 1;
118 x++;
119 }
120 else
121 {
122 f = f - 2 * y + 1;
123 y--;
124 }
125 }
126}
|
改进的中点划线算法和正负法虽然都避免了浮点运算,并且计算判别式时用到的乘法都是乘2运算,可以用移位代替,但是实际效率缺有很大差别。因为正负法并不是严格按照x方向步进的,因此就会出现在某个点的下一个点在两个位置上重复画点的问题,增加了不必要的计算。此外,从生成圆的质量看,中点画圆法和改进的中点画圆法都比正负法效果好。
4、 快速画圆法
除了中点画圆法和正负法,本文再介绍一种圆的光栅扫描算法,就是快速画圆法。快速画圆法的生成效果和中点画圆法差不多,但是判别式的计算只用了加减法,没有用任何乘法,因此被成为快速画圆法。我找不到快速画圆法的理论依据,只是把算法的实现写出来,供有兴趣的读者参考。以下就是快速画圆法的实现算法:
128void Fast_Circle(int xc , int yc , int r)
129{
130 int x, y, d;
131
132 x = 0;
133 y = r;
134 d = -r / 2;
135 CirclePlot(xc , yc , x , y);
136 if(r % 2 == 0)
137 {
138 while(x < y)
139 {
140 x++;
141 if(d < 0)
142 d += x;
143 else
144 {
145 y--;
146 d += x - y;
147 }
148
149 CirclePlot(xc , yc , x , y);
150 }
151 }
152 else
153 {
154 while(x < y)
155 {
156 x++;
157 if(d < 0)
158 d += x + 1;
159 else
160 {
161 y--;
162 d += x - y + 1;
163 }
164
165 CirclePlot(xc , yc , x , y);
166 }
167 }
168}
|
圆的光栅扫描转换算法有很多种,本文介绍的几个都是简单易懂的算法,除了本文介绍的几种方法外,还有很多种圆光栅转换算法,比如多边形逼近算法等等,有兴趣的读者可以参考计算机图形学方面的资料自己研究算法的实现。
参考资料:
【1】计算几何:算法设计与分析 周培德 清华大学出版社 2005年
【2】计算几何:算法与应用 德贝尔赫(邓俊辉译) 清华大学出版社 2005年
【3】计算机图形学 孙家广、杨常贵 清华大学出版社 1995年
分享到:













相关推荐
### 圆生成算法 1. **Midpoint Circle Algorithm(中点圆算法)**:由Floyd提出的,基于错误扩散原理。从圆心开始,每次计算圆周上一个新点的位置,并判断是否需要填充该点及其相邻的四个点。算法效率高,适用于...
### 差分迭代圆生成算法 #### 摘要与背景 本文介绍了一种改进的圆生成算法——差分迭代圆生成算法。在计算机图形学领域,尤其是涉及到光栅图像处理时,圆作为基本图形元素之一,其绘制算法至关重要。传统上,中点...
在本场景中,"verilog Bresenham算法生成圆"指的是使用Verilog语言实现Bresenham算法来在硬件级别生成圆形的图像。 Bresenham算法是一种用于绘制简单二维图形的有效算法,特别是在低分辨率的像素画图中,如在计算机...
### 计算机图形学——第三讲:直线与圆生成算法 #### 一、图元的概念 图元作为计算机图形学中的基本元素,是构建复杂图形的基础。它们是不可再分的基本图形实体,例如点、直线、圆弧、多边形、字体符号以及位图等...
给定一系列圆的半径,目标是找到一种排列方式,使得这些圆在矩形框内放置时,每个圆都与矩形底边相切,同时排列的总长度最小。这种问题可以转化为一个回溯搜索的过程,通过构造一棵排列树来穷举所有可能的排列方案。...
在实际编程中,可以先设定圆的半径r,然后根据上述步骤生成一系列点,这些点构成的像素连接起来就可以形成一个近似的圆形。Bresenham算法的效率很高,因为它只进行简单的整数运算,避免了浮点运算带来的性能损失。 ...
3. 中心圆算法: 中心圆算法是一种用于绘制圆形的方法,它从圆心出发,通过迭代增加半径来确定圆上的像素点。在每一步,算法检查当前半径是否能覆盖下一个像素,如果可以,就画上这个像素,并更新半径。这种算法的...
本篇文章将深入探讨MFC中用于绘制圆和椭圆的三种主要算法:中点画圆算法、中点画椭圆算法以及Bresenham画圆算法。 首先,让我们从最基础的开始,中点画圆算法。这个算法基于极坐标系统,从圆心出发,逐步向外扩展...
实验中,你会看到代码部分可能包含了这些算法的实现,以及如何根据这些算法生成效果图。文档部分则可能详细解释了每一步的逻辑和算法背后的数学原理,帮助你理解为什么这样做可以得到正确的结果。 在进行扫描转换时...
对于圆的生成,我们可以利用费舍尔-约旦算法(Floyd-Steinberg dithering)或者Midpoint Circle Algorithm。Midpoint Circle Algorithm,也叫中点圆算法,是由丹尼斯·希尔(Dennis M. Ritchie)提出的,它通过迭代...
Delaunay三角网格生成算法是一种广泛应用的网格生成方法,它能确保生成的三角形满足特定的优化条件。 Delaunay三角网是一种特殊的三角网格,其中任意一个三角形的内切圆不包含其他任何点。这一特性使得Delaunay三角...
本文详细介绍了基本图形生成算法中的几个关键部分,包括直线、圆、椭圆的生成算法,以及曲线处理、图形裁剪和消影等技术。这些算法和技术构成了现代计算机图形学的基础,对于理解和开发复杂的图形渲染系统至关重要。
5. **填充与闭合**: 如果需要填充椭圆弧,可以使用扫描线填充算法,根据椭圆弧的边界生成一系列水平线,并用颜色填充这些线之间的区域。最后,如果椭圆弧不是完整的圆,需要通过直线或其他方式闭合路径。 在实现...
3. Mitchell-Netravali算法:这是一种高质量的抗锯齿圆形和椭圆生成算法,它使用了更复杂的数学公式来平滑边缘,使得图形在视觉上更为平滑。 三、填充算法 4.扫描线填充算法:这种方法通过逐行检查像素是否位于...
在这个大作业中,我们看到作者使用C++编程语言实现了一系列经典的计算机图形学算法,包括直线绘制、圆形与椭圆的生成以及图形的裁剪方法。下面将详细解释这些知识点。 1. **直线绘制算法**: - **DDA(Digital ...
delaunay三角生成算法是一种在二维空间中构造三角网格的重要技术,广泛应用于地理信息系统、计算机图形学、有限元分析等领域。VC++(Microsoft Foundation Classes)是微软提供的C++编程框架,用于开发Windows平台的...
涉及矩阵链相乘问题、投资问题、背包问题、旅行商问题(TSP)、数字三角形、哈夫曼编码、顾客等待时间最短问题、最小生成树问题、图着色问题、八皇后问题、连续邮资问题、卫兵布置问题、圆排列问题、最近对问题、...
根据提供的文件信息,我们可以深入探讨计算机图形学中的几个核心算法:直线生成算法、圆生成算法、椭圆生成算法以及剪裁算法。这些算法在计算机图形学领域有着广泛的应用,不仅适用于理论研究,还广泛用于软件开发、...
在"计算机图形学实验二(基本图形生成算法)"中,我们通常会接触到一系列核心概念和技术,这些技术和算法是构建现代游戏、动画、虚拟现实等应用的基础。以下是该实验可能涉及的一些关键知识点: 1. **坐标系统**:...
然后,利用Bresenham直线算法的变体来生成这些圆弧的像素点。 在MFC中,我们可以使用CDC(Device Context)类来操作图形,如绘制像素。首先,我们需要创建一个CDC对象,然后选择一个合适的画笔和刷子来设定线条颜色...