素数算法

题目：

写一个程序，找出前N个素数。比如N为100，则找出前100个素数。

分析

最基本的想法就是对1到N得每个数进行判断，如果是素数则输出。一种改进的方法是不需要对1到N所有的数都进行判断，因为偶数肯定不是素数，而奇数可能是素数，可能不是。2，3，5都是素数，这可以直接得到。然后我们可以跳过2与3的倍数，即对于6n，6n+1, 6n+2, 6n+3, 6n+4, 6n+5，我们只需要判断6n+1与6n+5是否是素数即可。

判断某个数m是否是素数，最基本的方法就是对2到m-1之间的数整除m，如果有一个数能够整除m，则m就不是素数。判断m是否是素数还可以进一步改进，不需要对2到m-1之间的数全部整除m，只需要对2到根号m之间的数整除m就可以。如用2，3，4，5...根号m整除m。其实这还是有浪费，因为如果2不能整除，则2的倍数也不能整除，同理3不能整除则3的倍数也不能整除，因此可以只用2到根号m之间小于根号m的素数去除即可。

解法1：基本解法

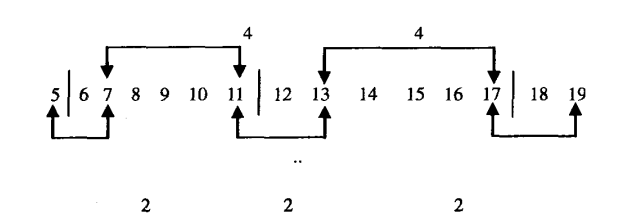
给出一个最基本的解法就是预先可得2，3，5为素数，然后跳过2与3的倍数，从7开始，然后判断11，然后判断13，再是17...规律就是从5加2，然后加4，然后加2，然后再加4。如此反复即可，如下图所示，只需要判断7，11，13，17，19，23，25，29...这些数字。对这些数进行判断，如果是素数则输出。

判断是否是素数采用改进后的方案，即对2到根号m之间的数整除m来进行判断。需要注意一点，不能直接用根号m判断，因为对于某些数字，比如121，开根号后得到的不一定是11，可能是10.999999，所以最好使用乘法判断，如代码中所示：

#include  <stdio.h>

#define   MAXSIZE    100
#define   YES          1
#define   NO           0

int main(void)
{
     int  prime[MAXSIZE];     /* array to contains primes */
     int  gap = 2;            /* increasing gap = 2 and 4 */
     int  count = 3;          /* no. of primes            */
     int  may_be_prime = 5;   /* working  variable        */
     int  i, is_prime;

     prime[0] = 2;            /* Note that 2, 3 and 5 are */
     prime[1] = 3;            /* primes.                  */
     prime[2] = 5;
     while (count < MAXSIZE)  { /* loop until prime[] full*/
          may_be_prime += gap;  /* get next number        */
          gap           = 6 - gap; /* switch to next gap  */
          is_prime      = YES;  /* suppose it were a prime*/
          for (i = 2; prime[i]*prime[i] <= may_be_prime && is_prime; i++)
               if (may_be_prime % prime[i] == 0) /* NO    */
                    is_prime = NO; /* exit                */
          if (is_prime)       /* if it IS a prime...      */
               prime[count++] = may_be_prime;  /* save it */
     }

     printf("\nPrime Number Generation Program");
     printf("\n===============================\n");
     printf("\nFirst %d Prime Numbers are :\n", count);
     for (i = 0; i < count; i++) {
          if (i % 10 == 0) printf("\n");
          printf("%5d", prime[i]);
     }
     return 0;
}

解法2：筛选法

用一个数组x[]存储3，5，7...这些奇数，则x[i]存的就是2i+3，这样初始设置所有数都没有筛掉，然后逐次把合数筛掉。实际就是把2i+3的倍数筛掉，2i+3的倍数可以写成(2i+3)j，j>1，不然j=1会筛掉自己。又由于偶数不用考虑，所以筛掉的数应该为(2n+1)(2i+3)=2[n(2i+3)+i]+3。因此要筛掉的数在数组中的位置为n(2i+3)+i，n=1，2，3...n=1时，这个值就是2i+3+i，n=2时为2(2i+3)+i；如果一共有N个元素，则x[]中最后一个元素x[N-1]=2N+3，由此就可以得到2到2N+3之间所有素数。代码如下，注意下面的代码并不是求前200个素数，而是求的从2到403之间的素数。

/* ------------------------------------------------------ */
/* FUNCTION sieve :                                       */
/*    This program uses Eratosthenes Sieve method to      */
/* generate all primes between 2 and MAXSIZE*2+3.  This   */
/* is a very simple yet elegant method to generate primes */
/*                                                        */
/* Copyright Ching-Kuang Shene               July/01/1989 */
/* ------------------------------------------------------ */

#include  <stdio.h>

#define   MAXSIZE   200
#define   DELETED     1
#define   KEPT        0

void main(void)
{
     int  sieve[MAXSIZE+1];   /* the sieve array          */
     int  count = 1;          /* no. of primes counter    */
     int  prime;              /* a generated prime        */
     int  i, k;               /* working variable         */

     printf("\nEratosthenes Sieve Method");
     printf("\n=========================");
     printf("\n\nPrime Numbers between 2 and %d\n", MAXSIZE*2+3);

     for (i = 0; i <= MAXSIZE; i++) /* set all items to be*/
          sieve[i] = KEPT;    /* kept in the sieve        */

     for (i = 0; i <= MAXSIZE; i++) /* for each i, it     */
          if (sieve[i] == KEPT) {   /* corresponds to 2i+3*/
               prime = i + i + 3;   /* if it is not sieved*/
               count++;             /* prime=2i+3.        */
               for (k = prime + i; k <= MAXSIZE; k += prime)
                    sieve[k] = DELETED; /* screen multiple*/
          }

     printf("\n%6d", 2);      /* output part.             */
     for (i = 0, k = 2; i <= MAXSIZE; i++)
          if (sieve[i] == KEPT) {
               if (k > 10) {
                    printf("\n");
                    k = 1;
               }
               printf("%6d", 2*i+3);
               k++;
          }
     printf("\n\nThere are %d primes in total.", count);
}