жСШељХиЗ™пЉЪ
http://www.blogjava.net/zhenandaci/archive/2009/02/13/254519.html
дЄКеЫЮиѓіеИ∞еѓєдЇОжЦЗжЬђеИЖз±їињЩж†ЈзЪДдЄНйАВеЃЪйЧЃйҐШпЉИжЬЙдЄАдЄ™дї•дЄКиІ£зЪДйЧЃйҐШзІ∞дЄЇдЄНйАВеЃЪйЧЃйҐШпЉЙпЉМйЬАи¶БжЬЙдЄАдЄ™жМЗж†ЗжЭ•и°°йЗПиІ£еЖ≥жЦєж°ИпЉИеН≥жИСдїђйАЪињЗиЃ≠зїГеїЇзЂЛзЪДеИЖз±їж®°еЮЛпЉЙзЪДе•љеЭПпЉМиАМеИЖз±їйЧійЪФжШѓдЄАдЄ™жѓФиЊГе•љзЪДжМЗж†ЗгАВ
еЬ®ињЫи°МжЦЗжЬђеИЖз±їзЪДжЧґеАЩпЉМжИСдїђеПѓдї•иЃ©иЃ°зЃЧжЬЇињЩж†ЈжЭ•зЬЛеЊЕжИСдїђжПРдЊЫзїЩеЃГзЪДиЃ≠зїГж†ЈжЬђпЉМжѓПдЄАдЄ™ж†ЈжЬђзФ±дЄАдЄ™еРСйЗПпЉИе∞±жШѓйВ£дЇЫжЦЗжЬђзЙєеЊБжЙАзїДжИРзЪДеРСйЗПпЉЙеТМдЄАдЄ™ж†ЗиЃ∞пЉИж†Зз§ЇеЗЇињЩдЄ™ж†ЈжЬђе±ЮдЇОеУ™дЄ™з±їеИЂпЉЙзїДжИРгАВе¶ВдЄЛпЉЪ
Di=(xi,yi)
xiе∞±жШѓжЦЗжЬђеРСйЗПпЉИзїіжХ∞еЊИйЂШпЉЙпЉМyiе∞±жШѓеИЖз±їж†ЗиЃ∞гАВ
еЬ®дЇМеЕГзЪДзЇњжАІеИЖз±їдЄ≠пЉМињЩдЄ™и°®з§ЇеИЖз±їзЪДж†ЗиЃ∞еП™жЬЙдЄ§дЄ™еАЉпЉМ1еТМ-1пЉИзФ®жЭ•и°®з§Їе±ЮдЇОињШжШѓдЄНе±ЮдЇОињЩдЄ™з±їпЉЙгАВжЬЙдЇЖињЩзІНи°®з§Їж≥ХпЉМжИСдїђе∞±еПѓдї•еЃЪдєЙдЄАдЄ™ж†ЈжЬђзВєеИ∞жЯРдЄ™иґЕеє≥йЭҐзЪДйЧійЪФпЉЪ
ќіi=yi(wxi+b)
ињЩдЄ™еЕђеЉПдєНдЄАзЬЛж≤°дїАдєИз•ЮзІШзЪДпЉМдєЯиѓідЄНеЗЇдїАдєИйБУзРЖпЉМеП™жШѓдЄ™еЃЪдєЙиАМеЈ≤пЉМдљЖжИСдїђеБЪеБЪеПШжНҐпЉМе∞±иГљзЬЛеЗЇдЄАдЇЫжЬЙжДПжАЭзЪДдЄЬи•њгАВ
й¶ЦеЕИж≥®жДПеИ∞е¶ВжЮЬжЯРдЄ™ж†ЈжЬђе±ЮдЇОиѓ•з±їеИЂзЪДиѓЭпЉМйВ£дєИwxi+b>0пЉИиЃ∞еЊЧдєИпЉЯињЩжШѓеЫ†дЄЇжИСдїђжЙАйАЙзЪДg(x)=wx+bе∞±йАЪињЗе§ІдЇО0ињШжШѓе∞ПдЇО0жЭ•еИ§жЦ≠еИЖз±їпЉЙпЉМиАМyiдєЯе§ІдЇО0пЉЫиЛ•дЄНе±ЮдЇОиѓ•з±їеИЂзЪДиѓЭпЉМйВ£дєИwxi+b<0пЉМиАМyiдєЯе∞ПдЇО0пЉМињЩжДПеС≥зЭАyi(wxi+b)жАїжШѓе§ІдЇО0зЪДпЉМиАМдЄФеЃГзЪДеАЉе∞±з≠ЙдЇО|wxi+b|пЉБпЉИдєЯе∞±жШѓ|g(xi)|пЉЙ
зО∞еЬ®жККwеТМbињЫи°МдЄАдЄЛељТдЄАеМЦпЉМеН≥зФ®w/||w||еТМb/||w||еИЖеИЂдї£жЫњеОЯжЭ•зЪДwеТМbпЉМйВ£дєИйЧійЪФе∞±еПѓдї•еЖЩжИР
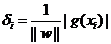
ињЩдЄ™еЕђеЉПжШѓдЄНжШѓзЬЛдЄКеОїжЬЙзВєзЬЉзЖЯпЉЯж≤°йФЩпЉМињЩдЄНе∞±жШѓиІ£жЮРеЗ†дљХдЄ≠зВєxiеИ∞зЫізЇњg(x)=0зЪДиЈЭз¶їеЕђеЉПеШЫпЉБпЉИжО®еєњдЄАдЄЛпЉМжШѓеИ∞иґЕеє≥йЭҐg(x)=0зЪДиЈЭз¶їпЉМ g(x)=0е∞±жШѓдЄКиКВдЄ≠жПРеИ∞зЪДеИЖз±їиґЕеє≥йЭҐпЉЙ
е∞ПTipsпЉЪ||w||жШѓдїАдєИзђ¶еПЈпЉЯ||w||еПЂеБЪеРСйЗПwзЪДиМГжХ∞пЉМиМГжХ∞жШѓеѓєеРСйЗПйХњеЇ¶зЪДдЄАзІНеЇ¶йЗПгАВжИСдїђеЄЄиѓізЪДеРСйЗПйХњеЇ¶еЕґеЃЮжМЗзЪДжШѓеЃГзЪД2-иМГжХ∞пЉМиМГжХ∞жЬАдЄАиИђзЪД谮积嚥еЉПдЄЇp-иМГжХ∞пЉМеПѓдї•еЖЩжИРе¶ВдЄЛи°®иЊЊеЉП
еРСйЗПw=(w1, w2, w3,вА¶вА¶ wn)
еЃГзЪДp-иМГжХ∞дЄЇ
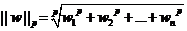
зЬЛзЬЛжККpжНҐжИР2зЪДжЧґеАЩпЉМдЄНе∞±жШѓдЉ†зїЯзЪДеРСйЗПйХњеЇ¶дєИпЉЯељУжИСдїђдЄНжМЗжШОpзЪДжЧґеАЩпЉМе∞±еГП||w||ињЩж†ЈдљњзФ®жЧґпЉМе∞±жДПеС≥зЭАжИСдїђдЄНеЕ≥ењГpзЪДеАЉпЉМзФ®еЗ†иМГжХ∞йГљеПѓдї•пЉЫжИЦиАЕдЄКжЦЗеЈ≤зїПжПРеИ∞дЇЖpзЪДеАЉпЉМдЄЇдЇЖеПЩињ∞жЦєдЊњдЄНеЖНйЗНе§НжМЗжШОгАВ
ељУзФ®ељТдЄАеМЦзЪДwеТМbдї£жЫњеОЯеАЉдєЛеРОзЪДйЧійЪФжЬЙдЄАдЄ™дЄУйЧ®зЪДеРНзІ∞пЉМеПЂеБЪеЗ†дљХйЧійЪФпЉМеЗ†дљХйЧійЪФжЙАи°®з§ЇзЪДж≠£жШѓзВєеИ∞иґЕеє≥йЭҐзЪДжђІж∞ПиЈЭз¶їпЉМжИСдїђдЄЛйЭҐе∞±зЃАзІ∞еЗ†дљХйЧійЪФдЄЇвАЬиЈЭз¶ївАЭгАВдї•дЄКжШѓеНХдЄ™зВєеИ∞жЯРдЄ™иґЕеє≥йЭҐзЪДиЈЭз¶їпЉИе∞±жШѓйЧійЪФпЉМеРОйЭҐдЄНеЖНеМЇеИЂињЩдЄ§дЄ™иѓНпЉЙеЃЪдєЙпЉМеРМж†ЈеПѓдї•еЃЪдєЙдЄАдЄ™зВєзЪДйЫЖеРИпЉИе∞±жШѓдЄАзїДж†ЈжЬђпЉЙеИ∞жЯРдЄ™иґЕеє≥йЭҐзЪДиЈЭз¶їдЄЇж≠§йЫЖеРИдЄ≠з¶їиґЕеє≥йЭҐжЬАињСзЪДзВєзЪДиЈЭз¶їгАВдЄЛйЭҐињЩеЉ†еЫЊжЫіеК†зЫіиІВзЪДе±Хз§ЇеЗЇдЇЖеЗ†дљХйЧійЪФзЪДзО∞еЃЮеРЂдєЙпЉЪ
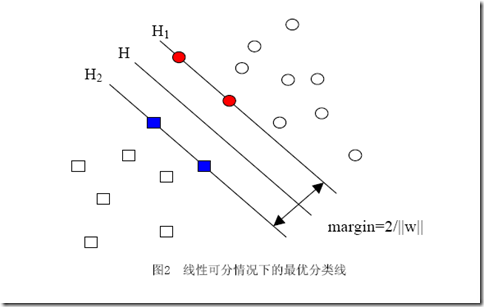
HжШѓеИЖз±їйЭҐпЉМиАМH1еТМH2жШѓеє≥и°МдЇОHпЉМдЄФињЗз¶їHжЬАињСзЪДдЄ§з±їж†ЈжЬђзЪДзЫізЇњпЉМH1дЄОHпЉМH2дЄОHдєЛйЧізЪДиЈЭз¶їе∞±жШѓеЗ†дљХйЧійЪФгАВ
дєЛжЙАдї•е¶Вж≠§еЕ≥ењГеЗ†дљХйЧійЪФињЩдЄ™дЄЬи•њпЉМжШѓеЫ†дЄЇеЗ†дљХйЧійЪФдЄОж†ЈжЬђзЪДиѓѓеИЖжђ°жХ∞йЧіе≠ШеЬ®еЕ≥з≥їпЉЪ

еЕґдЄ≠зЪДќіжШѓж†ЈжЬђйЫЖеРИеИ∞еИЖз±їйЭҐзЪДйЧійЪФпЉМR=max ||xi|| i=1,...,nпЉМеН≥RжШѓжЙАжЬЙж†ЈжЬђдЄ≠пЉИxiжШѓдї•еРСйЗПи°®з§ЇзЪДзђђiдЄ™ж†ЈжЬђпЉЙеРСйЗПйХњеЇ¶жЬАйХњзЪДеАЉпЉИдєЯе∞±жШѓиѓідї£и°®ж†ЈжЬђзЪДеИЖеЄГжЬЙе§ЪдєИеєњпЉЙгАВеЕИдЄНењЕињљз©ґиѓѓеИЖжђ°жХ∞зЪДеЕЈдљУеЃЪдєЙеТМжО®еѓЉињЗз®ЛпЉМеП™и¶БиЃ∞еЊЧињЩдЄ™иѓѓеИЖжђ°жХ∞дЄАеЃЪз®ЛеЇ¶дЄКдї£и°®еИЖз±їеЩ®зЪДиѓѓеЈЃгАВиАМдїОдЄКеЉПеПѓдї•зЬЛеЗЇпЉМиѓѓеИЖжђ°жХ∞зЪДдЄКзХМзФ±еЗ†дљХйЧійЪФеЖ≥еЃЪпЉБпЉИељУзДґпЉМжШѓж†ЈжЬђеЈ≤зЯ•зЪДжЧґеАЩпЉЙ
иЗ≥ж≠§жИСдїђе∞±жШОзЩљдЄЇдљХи¶БйАЙжЛ©еЗ†дљХйЧійЪФжЭ•дљЬдЄЇиѓДдїЈдЄАдЄ™иІ£дЉШеК£зЪДжМЗж†ЗдЇЖпЉМеОЯжЭ•еЗ†дљХйЧійЪФиґКе§ІзЪДиІ£пЉМеЃГзЪДиѓѓеЈЃдЄКзХМиґКе∞ПгАВеЫ†ж≠§жЬАе§ІеМЦеЗ†дљХйЧійЪФжИРдЇЖжИСдїђиЃ≠зїГйШґжЃµзЪДзЫЃж†ЗпЉМиАМдЄФпЉМдЄОдЇМжККеИАдљЬиАЕжЙАеЖЩзЪДдЄНеРМпЉМжЬАе§ІеМЦеИЖз±їйЧійЪФеєґдЄНжШѓSVMзЪДдЄУеИ©пЉМиАМжШѓжЧ©еЬ®зЇњжАІеИЖз±їжЧґжЬЯе∞±еЈ≤жЬЙзЪДжАЭжГ≥гАВ
еИЖдЇЂеИ∞пЉЪ








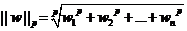





зЫЄеЕ≥жО®иНР
### SVMеЕ•йЧ®пЉИдЇФпЉЙзЇњжАІеИЖз±їеЩ®зЪДж±ВиІ£вАФвАФйЧЃйҐШзЪДжППињ∞Part2 #### йЗНи¶Бж¶ВењµдЄОиГМжЩѓ жЬђжЦЗж°£жЧ®еЬ®еЄЃеК©иѓїиАЕзРЖиІ£жФѓжМБеРСйЗПжЬЇ(SVM)дЄ≠зЪДзЇњжАІеИЖз±їеЩ®ж±ВиІ£ињЗз®ЛеПКеЕґжХ∞е≠¶и°®ињ∞пЉМзЙєеИЂеЕ≥ж≥®дЇОе¶ВдљХе∞ЖзЇњжАІеИЖз±їеЩ®йЧЃйҐШиљђеМЦдЄЇдЉШеМЦйЧЃйҐШпЉМеєґиЃ®иЃЇ...
дїОзїЩеЗЇзЪДеЖЕеЃєзЙЗжЦ≠дЄ≠пЉМжИСдїђеПѓдї•дЇЖиІ£еИ∞жЦЗж°£иЃ®иЃЇдЇЖеѓєжКЧжФїеЗїпЉИEvasion AttacksпЉЙпЉМзЙєеИЂжШѓйТИеѓєзЇњжАІеИЖз±їеЩ®еТМйЭЮзЇњжАІеИЖз±їеЩ®зЪДзїХињЗжФїеЗїпЉИEvasion of ClassifiersпЉЙпЉМдї•еПКе¶ВдљХж£АжµЛжБґжДПPDFжЦЗдїґгАВ жЦЗж°£еЉАзѓЗеЉХзФ®дЇЖгАКе≠Ще≠РеЕµж≥ХгАЛдЄ≠...
зДґеРОжШѓзЇњжАІеИЖз±їеЩ®пЉМе¶ВжФѓжМБеРСйЗПжЬЇпЉИSVMпЉЙеТМжДЯзЯ•еЩ®гАВзЇњжАІеИЖз±їеЩ®еЫ†еЕґзЃАжіБзЪДжХ∞е≠¶ељҐеЉПеТМйЂШжХИзЪДиЃ°зЃЧиАМе§ЗеПЧйЭТзЭРгАВеЃГдїђйАЪињЗеЬ®зЙєеЊБз©ЇйЧідЄ≠жЙЊеИ∞дЄАдЄ™иґЕеє≥йЭҐжЭ•еИТеИЖдЄНеРМз±їеИЂзЪДж†ЈжЬђгАВзЇњжАІSVMеѓїжЙЊжЬАе§ІзЪДйЧійЪФиЊєзХМпЉМдї•жЬАе§ІеМЦдЄ§з±їж†ЈжЬђ...
зЇњжАІеИЖз±їеЩ®е¶ВиіЭеПґжЦѓеИЖз±їеЩ®пЉМиГље§ЯжПРдЊЫеЯЇдЇОж¶ВзОЗзЪДеЖ≥з≠ЦиЊєзХМгАВйЭЮзЇњжАІеИЖз±їеЩ®еИЩеМЕжЛђе§Ъе±ВжДЯзЯ•еЩ®гАБеЖ≥з≠Цж†СеТМеЊДеРСеЯЇзљСзїЬпЉИRHзљСзїЬпЉЙгАВињЩдЇЫйЭЮзЇњжАІж®°еЮЛйАЪеЄЄиГље§Яе§ДзРЖжЫіе§НжЭВзЪДжХ∞жНЃеЕ≥з≥їпЉМйАВеЇФжЫіеєњж≥ЫзЪДеЃЮйЩЕеЇФзФ®гАВ ж≠§е§ЦпЉМжЬђдє¶ињШжґЙеПКдЄК...
Part 1еПѓиГљдїЛзїНдЇЖжЬізі†иіЭеПґжЦѓеИЖз±їеЩ®зЪДеЯЇжЬђеОЯзРЖеТМеЇФзФ®еЬЇжЩѓпЉМиАМPart 2еПѓиГљжЈ±еЕ•еИ∞жЭ°дїґзЛђзЂЛеБЗиЃЊгАБиіЭеПґжЦѓзљСзїЬдї•еПКеЬ®жЦЗжЬђеИЖз±їеТМжО®иНРз≥їзїЯдЄ≠зЪДеЇФзФ®гАВ жАїзЪДжЭ•иѓіпЉМињЩдЇЫиѓЊдїґжПРдЊЫдЇЖдЄ∞еѓМзЪДжЬЇеЩ®е≠¶дє†еТМдЇЇеЈ•жЩЇиГљеЯЇз°АзЯ•иѓЖпЉМжґµзЫЦдЇЖдїО...
1. зїЯиЃ°ж®°еЉПиѓЖеИЂпЉЪеИ©зФ®ж¶ВзОЗж®°еЮЛпЉМе¶ВжЬізі†иіЭеПґжЦѓеИЖз±їеЩ®пЉМжЭ•иѓЖеИЂжХ∞жНЃдЄ≠зЪДж®°еЉПгАВ 2. еЯЇдЇОеЃЮдЊЛзЪДе≠¶дє†пЉЪеМЕжЛђKињСйВїпЉИK-NNпЉЙзЃЧж≥ХпЉМйАЪињЗжЯ•жЙЊдЄОжЦ∞ж†ЈжЬђжЬАзЫЄдЉЉзЪДиЃ≠зїГж†ЈжЬђжЭ•еБЪеЗЇеЖ≥з≠ЦгАВ 3. з•ЮзїПзљСзїЬеТМжЈ±еЇ¶е≠¶дє†пЉЪйАЪињЗе§Ъе±ВйЭЮзЇњжАІ...
жЬізі†иіЭеПґжЦѓеИЖз±їеЩ®жШѓдЄАзІНеЯЇдЇОж¶ВзОЗзЪДеИЖз±їжЦєж≥ХпЉМеЃГеИ©зФ®иіЭеПґжЦѓеЃЪзРЖжЭ•иЃ°зЃЧзїЩеЃЪжХ∞жНЃзЪДжЭ°дїґдЄЛе±ЮдЇОжЯРдЄАз±їзЪДж¶ВзОЗгАВиѓ•зЃЧж≥ХзЪДеЙНжПРеБЗиЃЊжШѓзЙєеЊБдєЛйЧізЫЄдЇТзЛђзЂЛпЉМињЩж†ЈеПѓдї•зЃАеМЦиЃ°зЃЧињЗз®ЛгАВ еЖ≥з≠Цж†СжШѓдЄАзІНеی嚥еМЦзЪДеЖ≥з≠ЦжФѓжМБеЈ•еЕЈпЉМдї•ж†СзКґ...
жО•дЄЛжЭ•пЉМ"Part 2 Linear model.pdf"жОҐиЃ®дЇЖзЇњжАІж®°еЮЛпЉМињЩжШѓжЬЇеЩ®е≠¶дє†дЄ≠жЬАеЯЇз°АдЄФеЃЮзФ®зЪДжЦєж≥ХдєЛдЄАгАВзЇњжАІж®°еЮЛе¶ВйАїиЊСеЫЮељТеТМзЇњжАІеЫЮељТпЉМеЃГдїђеЬ®йҐДжµЛеИЖжЮРдЄ≠еєњж≥ЫдљњзФ®пЉМеЫ†дЄЇеЃГдїђжШУдЇОзРЖиІ£еТМеЃЮзО∞гАВињЩйГ®еИЖеПѓиГљдЉЪиЃ≤иІ£е¶ВдљХжЮДеїЇеТМдЉШеМЦ...
3. **зђђеЕ≠иЃ≤пЉЪиіЭеПґжЦѓеИЖз±їеЩ®еПКеЕґжФєињЫ** - иіЭеПґжЦѓеИЖз±їжШѓж¶ВзОЗжО®зРЖзЪДдЄАзІНеЇФзФ®пЉМжЬђиЃ≤жЈ±еЕ•иЃ≤иІ£дЇЖжЬізі†иіЭеПґжЦѓеИЖз±їеЩ®зЪДеОЯзРЖеТМе±АйЩРжАІпЉМеєґжОҐиЃ®дЇЖе§Ъй°єеЉПеИЖеЄГгАБжЛЙжЩЃжЛЙжЦѓеє≥жїСз≠ЙжФєињЫжЦєж≥ХгАВ 4. **зђђдЄГиЃ≤пЉЪйАїиЊСеЫЮељТ** - йАїиЊСеЫЮељТжШѓдЄА...
DPMйАЪеЄЄеЯЇдЇОBoostingж°ЖжЮґпЉМйАЪињЗдЄАз≥їеИЧеЉ±еИЖз±їеЩ®пЉИе¶ВHaarзЙєеЊБжИЦHOGзЙєеЊБпЉЙзїДеРИжИРеЉЇеИЖз±їеЩ®пЉМдї•жПРйЂШж£АжµЛжАІиГљгАВ еЬ®еЃЮйЩЕеЇФзФ®дЄ≠пЉМжЈ±еЇ¶з•ЮзїПзљСзїЬзїПеЄЄдЄОеРДзІНжКАжЬѓзїУеРИпЉМдЊЛе¶ВдЄОеЊ™зОѓз•ЮзїПзљСзїЬпЉИRecurrent Neural Network, RNNпЉЙеТМ...
2. **дЇЇиДЄж£АжµЛ**пЉЪдљњзФ®е¶ВHaarзЙєеЊБзЇІиБФеИЖз±їеЩ®жИЦDPMпЉИDeformable Part ModelsпЉЙз≠ЙжЦєж≥Хж£АжµЛеЫЊеГПдЄ≠зЪДдЇЇиДЄеМЇеЯЯгАВ 3. **еІњжАБж†°ж≠£**пЉЪйАЪињЗжЧЛиљђеТМеє≥зІїж†°ж≠£еЫЊеГПпЉМдљњжЙАжЬЙдЇЇиДЄйГље§ДдЇОзЫЄдЉЉзЪДиІЖиІТгАВ 4. **ж®°еЮЛиЃ≠зїГ**пЉЪдљњзФ®SVM...
10. **AdaBoost**пЉЪйАЪињЗињ≠дї£иЃ≠зїГеЉ±еИЖз±їеЩ®пЉМжЮДеїЇеЉЇеИЖз±їеЩ®зЪДйЫЖжИРе≠¶дє†жЦєж≥ХгАВ 11. **йЪПжЬЇж£ЃжЮЧпЉИRandom ForestпЉЙ**пЉЪеМЕеРЂе§ЪдЄ™еЖ≥з≠Цж†СзЪДйЫЖжИРе≠¶дє†жЦєж≥ХпЉМжПРйЂШдЇЖйҐДжµЛзЪДз®≥еЃЪжАІеТМеЗЖз°ЃжАІгАВ 12. **дЄїжИРеИЖеИЖжЮРпЉИPrincipal Component...
2. **Part2: mlBasics_niloy.pdf** жЬЇеЩ®е≠¶дє†еЯЇз°АжШѓжЈ±еЇ¶е≠¶дє†зЪДеЯЇзЯ≥пЉМињЩйГ®еИЖеПѓиГљдЉЪиЃ≤иІ£зЫСзЭ£е≠¶дє†гАБжЧ†зЫСзЭ£е≠¶дє†еТМеЉЇеМЦе≠¶дє†зЪДеЯЇжЬђж¶ВењµпЉМдї•еПКеЄЄзФ®зЪДжЬЇеЩ®е≠¶дє†зЃЧж≥ХпЉМе¶ВзЇњжАІеЫЮељТгАБйАїиЊСеЫЮељТгАБеЖ≥з≠Цж†СгАБйЪПжЬЇж£ЃжЮЧеТМSVMз≠ЙгАВињЩдЇЫ...
жЬізі†иіЭеПґжЦѓеИЖз±їеЩ®еБЗиЃЊзЙєеЊБдєЛйЧізЫЄдЇТзЛђзЂЛпЉМиЩљзДґињЩдЄАеБЗиЃЊеЬ®еЃЮйЩЕеЇФзФ®дЄ≠еЊАеЊАдЄНжИРзЂЛпЉМдљЖиѓ•жЦєж≥ХзЃАеНХйЂШжХИпЉМйАВзФ®дЇОе§ІиІДж®°жХ∞жНЃйЫЖгАВ - **J48()**: C4.5еЖ≥з≠Цж†СзЃЧж≥ХгАВC4.5жШѓдЄАзІНзїПеЕЄзЪДеЖ≥з≠Цж†СзЃЧж≥ХпЉМеЃГеПѓдї•зФЯжИРжШУдЇОзРЖиІ£зЪДеЖ≥з≠ЦиІДеИЩпЉМ...
2. **дЇЇиДЄж£АжµЛ**пЉЪеЄЄзФ®зЪДдЇЇиДЄж£АжµЛжЦєж≥ХжЬЙHaarзЙєеЊБзЇІиБФеИЖз±їеЩ®гАБHOGпЉИHistogram of Oriented GradientsпЉЙеТМDPMпЉИDeformable Part ModelsпЉЙгАВMATLABдЄ≠зЪДvision.CascadeObjectDetectorеЗљжХ∞еПѓдї•еЃЮзО∞еЯЇдЇОHaarзЙєеЊБзЪДењЂйАЯдЇЇиДЄ...
дЊЛе¶ВпЉМBag of Words (BoW)ж®°еЮЛзїУеРИSIFTжИЦSURFзЙєеЊБпЉМйАЪињЗKMeansиБЪз±їзФЯжИРиІЖиІЙиѓНж±ЗпЉМеєґеИ©зФ®SVMињЫи°МеИЖз±їгАВз®АзЦПзЉЦз†Б(Sparse Coding)жЦєж≥Хе¶ВLLC(Locality-constrained Linear Coding)йАЪињЗе≠¶дє†е±АйГ®зЇњжАІи°®з§ЇжЭ•еѓєеЫЊеГПињЫи°МеИЖз±ї...
- **SoftmaxеИЖз±їеЩ®пЉЪ** е§Ъй°єеЉПйАїиЊСеЫЮељТзЪДдЄАзІН嚥еЉПпЉМзФ®дЇОе§ЪеИЖз±їдїїеК°гАВ **Optimization** - **з≠ЦзХ•1пЉЪйЪПжЬЇжРЬ糥** - еЬ®йҐДеЃЪдєЙзЪДиМГеЫіеЖЕйЪПжЬЇйАЙжЛ©иґЕеПВжХ∞гАВ - **з≠ЦзХ•2пЉЪж≤њзЭАжЦЬзОЗжЦєеРСеЙНињЫ** - дљњзФ®жХ∞еАЉжҐѓеЇ¶жИЦиІ£жЮР楃寶жЭ•...
дЉ†зїЯзЪДи°МдЇЇж£АжµЛжЦєж≥ХеМЕжЛђ Dalal з≠ЙдЇЇжПРеЗЇзЪД楃寶зЫіжЦєеЫЊпЉИHistogram of Oriented GradientпЉМHOGпЉЙдї•еПКдЄОзЇњжАІеИЖз±їеЩ®жФѓжМБеРСйЗПжЬЇпЉИSupport Vector MachineпЉМSVMпЉЙзїУеРИзЪДи°МдЇЇж£АжµЛжЦєж≥ХгАВ Felazenszwalb з≠ЙдЇЇйЪПеРОжПРеЗЇдЇЖжФєињЫзЪД...