Tree
二叉树
和其他树不同的是,二叉树的每个节点最多只有两个孩子节点,分别为左右孩子节点。
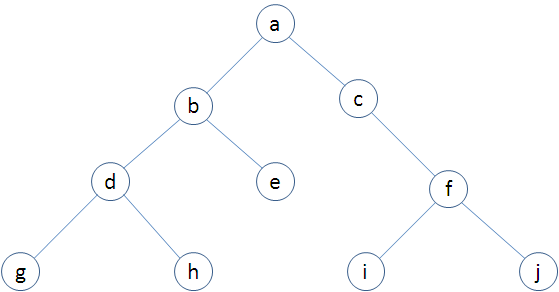
这是一棵二叉树,树的深度为4。
一棵深度为n的二叉树,最多有2的n次方-1个节点。
二叉树的第i层最多有2的i-1次方个节点。
如果度数为2的节点数为n2,则度数为0的节点,也就是叶子节点数为n2 + 1。即n0 = n2 + 1,n0为度数为0的节点数。
完全二叉树
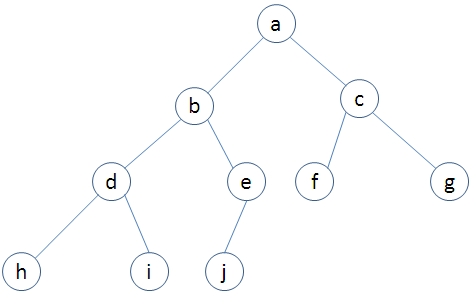
满二叉树
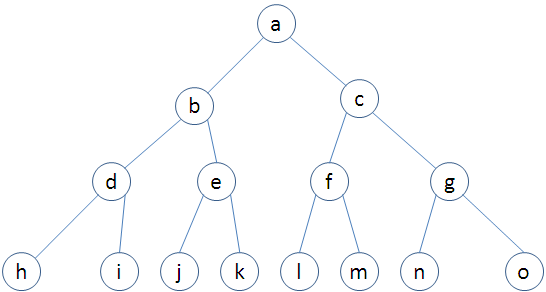
可以简单的通过一个数组来构造一个二叉树
typedef char btree_simple[];
构造一个二叉树
btree_simple btree = {'a', 'b', 'c', 'd', 'e', 'f', 'g', 0, 'h', 0, 'i', 'j', 'k'};
通过这样构造二叉树除了简单之外,还有一个好处就是这种构造二叉树的方式和广度优先遍历的结果一致。
typedef struct
{
char *ptr;
int size;
} btree_simple;
构造二叉树
int btree_simple_from(btree_simple *tree, int n, ...)
{
int i;
va_list vl;
tree->size = n;
tree->ptr = malloc(sizeof(int) * tree->size);
if (! tree->ptr)
{
return -1;
}
va_start(vl, n);
for (i = 0; i < n; i++)
{
tree->ptr[i] = (char) va_arg(vl, int);
}
va_end(vl);
return 0;
}
销毁也很简单
void btree_simple_free(btree_simple *tree)
{
if (tree)
{
free(tree->ptr);
}
}
遍历二叉树
二叉树遍历策略有深度优先遍历和广度优先遍历。
对于二叉树来说,将二叉树看成根,左子树,右子树,这样就有先序、中序、后序3种遍历方式。
递归方式
char * btree_simple_itr(btree_simple *tree, int *size, void (*callback) (btree_simple *, int, char **, int *))
{
char *result = NULL;
if (! size)
{
return NULL;
}
if (tree && tree->ptr)
{
*size = 0;
callback(tree, 0, &result, size);
}
return result;
}
先序
void btree_simple_iterate_callback_DLR(btree_simple *tree, int i, char **result, int *size)
{
int li = btree_simple_left(i);
int ri = btree_simple_right(i);
if (i < tree->size && tree->ptr[i])
{
*result = realloc(*result, sizeof(int) * ++(*size));
(*result)[(*size) - 1] = tree->ptr[i];
}
if (tree->ptr[li])
{
btree_simple_iterate_callback_DLR(tree, li, result, size);
}
if (tree->ptr[ri])
{
btree_simple_iterate_callback_DLR(tree, ri, result, size);
}
}
BTREE_SIMPLE_DLR
这是一个函数宏
#define BTREE_SIMPLE_DLR(P_TR, PZ) btree_simple_itr(P_TR, PZ, btree_simple_iterate_callback_DLR)
中序
void btree_simple_iterate_callback_LDR(btree_simple *tree, int i, char **result, int *size)
{
int li = btree_simple_left(i);
int ri = btree_simple_right(i);
if (tree->ptr[li])
{
btree_simple_iterate_callback_LDR(tree, li, result, size);
}
if (i < tree->size && tree->ptr[i])
{
*result = realloc(*result, sizeof(int) * ++(*size));
(*result)[(*size) - 1] = tree->ptr[i];
}
if (tree->ptr[ri])
{
btree_simple_iterate_callback_LDR(tree, ri, result, size);
}
}
BTREE_SIMPLE_LDR
这是一个函数宏
#define BTREE_SIMPLE_LDR(P_TR, PZ) btree_simple_itr(P_TR, PZ, btree_simple_iterate_callback_LDR)
后序
void btree_simple_iterate_callback_LRD(btree_simple *tree, int i, char **result, int *size)
{
int li = btree_simple_left(i);
int ri = btree_simple_right(i);
if (tree->ptr[li])
{
btree_simple_iterate_callback_LRD(tree, li, result, size);
}
if (tree->ptr[ri])
{
btree_simple_iterate_callback_LRD(tree, ri, result, size);
}
if (i < tree->size && tree->ptr[i])
{
*result = realloc(*result, sizeof(int) * ++(*size));
(*result)[(*size) - 1] = tree->ptr[i];
}
}
BTREE_SIMPLE_LRD
这是一个函数宏
#define BTREE_SIMPLE_LRD(P_TR, PZ) btree_simple_itr(P_TR, PZ, btree_simple_iterate_callback_LRD)
非递归方式
先序
int * btree_simple_list_pre2(btree_simple *tree, int *size)
{
int *result = NULL;
int *stack = NULL;
int top = 0, stack_size = 0;
if (! size)
{
return NULL;
}
if (tree && tree->ptr)
{
*size = 0;
stack = realloc(stack, sizeof(int) * ++stack_size);
stack[top] = 0;
top++;
while (top > 0)
{
while (top > 0 && stack[top - 1] < tree->size && tree->ptr[stack[top - 1]])
{
int li = btree_simple_left(stack[top - 1]);
result = realloc(result, sizeof(int) * ++(*size));
result[(*size) - 1] = tree->ptr[stack[top - 1]];
stack = realloc(stack, sizeof(int) * ++stack_size);
stack[top] = li;
top++;
}
top--;
if (top > 0)
{
int ri = btree_simple_right(stack[top - 1]);
top--;
stack = realloc(stack, sizeof(int) * ++stack_size);
stack[top] = ri;
top++;
}
}
free(stack);
}
return result;
}
中序
int * btree_simple_list_mid2(btree_simple *tree, int *size)
{
int *result = NULL;
int *stack = NULL;
int top = 0, stack_size = 0;
if (! size)
{
return NULL;
}
if (tree && tree->ptr)
{
*size = 0;
stack = realloc(stack, sizeof(int) * ++stack_size);
stack[top] = 0;
top++;
while (top > 0)
{
while (top > 0 && stack[top - 1] < tree->size && tree->ptr[stack[top - 1]])
{
int li = btree_simple_left(stack[top - 1]);
stack = realloc(stack, sizeof(int) * ++stack_size);
stack[top] = li;
top++;
}
top--;
if (top > 0)
{
int ri = btree_simple_right(stack[top - 1]);
result = realloc(result, sizeof(int) * ++(*size));
result[(*size) - 1] = tree->ptr[stack[top - 1]];
top--;
stack = realloc(stack, sizeof(int) * ++stack_size);
stack[top] = ri;
top++;
}
}
free(stack);
}
return result;
}
int main()
{
int i;
btree_simple btree;
char *list;
int size;
btree_simple_from(&btree, 13, 'a', 'b', 'c', 'd', 'e', 'f', 'g', NULL, 'h', NULL, 'i', 'j', 'k');
for (i = 0; i < btree.size; i++)
{
printf("%c%s", btree.ptr[i], i < btree.size - 1 ? " " : "\n");
}
list = BTREE_SIMPLE_DLR(&btree, &size);
printf("size=%d\n", size);
if (list && size > 0)
{
for (i = 0; i < size; i++)
{
if (list[i])
{
printf("%c%s", list[i], i < size - 1 ? " " : "\n");
}
}
}
if (list)
{
free(list);
}
list = btree_simple_list_pre2(&btree, &size);
printf("size=%d\n", size);
if (list && size > 0)
{
for (i = 0; i < size; i++)
{
if (list[i])
{
printf("%c%s", list[i], i < size - 1 ? " " : "\n");
}
}
}
if (list)
{
free(list);
}
list = BTREE_SIMPLE_LDR(&btree, &size);
printf("size=%d\n", size);
if (list && size > 0)
{
for (i = 0; i < size; i++)
{
if (list[i])
{
printf("%c%s", list[i], i < size - 1 ? " " : "\n");
}
}
}
if (list)
{
free(list);
}
list = btree_simple_list_mid2(&btree, &size);
printf("size=%d\n", size);
if (list && size > 0)
{
for (i = 0; i < size; i++)
{
if (list[i])
{
printf("%c%s", list[i], i < size - 1 ? " " : "\n");
}
}
}
if (list)
{
free(list);
}
list = BTREE_SIMPLE_LRD(&btree, &size);
printf("size=%d\n", size);
if (list && size > 0)
{
for (i = 0; i < size; i++)
{
if (list[i])
{
printf("%c%s", list[i], i < size - 1 ? " " : "\n");
}
}
}
if (list)
{
free(list);
}
btree_simple_free(&btree);
btree_simple_from(&btree, 13, 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'G', 'h', NULL, 'i', 'j', 'k');
list = btree_simple_list_pre2(&btree, &size);
printf("size=%d\n", size);
if (list && size > 0)
{
for (i = 0; i < size; i++)
{
if (list[i])
{
printf("%c%s", list[i], i < size - 1 ? " " : "\n");
}
}
}
if (list)
{
free(list);
}
btree_simple_free(&btree);
}
另外一种方式就是通过二叉链表来构造二叉树
struct node
{
char data;
struct node *left, *right;
};
typedef struct
{
struct node *root;
} btree;
R-Tree






相关推荐
**jsTree 中文文档概述** jsTree 是一个流行的JavaScript库,用于在网页上创建交互式的树状视图。它主要用于组织结构化的数据,如文件系统、数据库目录或自定义项目结构。jsTree 支持多种操作,包括点击、拖放、...
标题提到的"tree(c++ tree容器)"是一个第三方实现,旨在为C++开发者提供一个类似于STL接口的树容器,方便用户在项目中构建和操作树形数据。 这个源码库的亮点在于它的用法与C++标准库中的其他容器类似,如vector和...
设备树(Device Tree)在嵌入式Linux系统中扮演着至关重要的角色,它是一种数据结构,用于描述硬件配置,使得操作系统内核能够更好地理解和管理硬件资源。`device-tree-xlnx-master_tree_devicetree2018.3_`这个标题...
**jsTree API详解** jsTree 是一个流行的JavaScript库,用于创建、操作和展示交互式的HTML树状视图。它提供了一套丰富的API,使得开发者能够方便地实现树形结构的各种功能,如添加、删除、修改节点,以及节点的移动...
【速度树(SpeedTree)教程】 SpeedTree是一款广泛应用于游戏开发、影视特效、虚拟现实以及建筑设计等领域的高级树木和植被渲染软件。它以其强大的建模功能、高效的渲染技术和逼真的动态效果而闻名。本教程是专门...
TreeTagger是一款由德国图宾根大学的Philippe Schmid教授开发的著名自然语言处理工具,主要用于对文本进行词性标注、实体识别和句法分析。这个软件在学术界和工业界都得到了广泛的应用,特别是在语言学研究和信息...
其中,PowerTree作为一款专注于配电网络(PDN)设计的工具,正受到越来越多设计工程师和电源完整性工程师的青睐。它不仅提供了基于原理图的电源早期视图,还有助于优化PDN的设计与性能。本文将系统地介绍PowerTree...
在Flex中,Tree组件是用于显示层次结构数据的控件,而"flex带复选框的tree"(Flex CheckboxTree)则是对Tree组件的一种扩展,增加了复选框功能,用户可以对树形结构的节点进行选择或全选操作,常用于权限管理、配置...
在移动设备上,为了有效地展示层次结构数据,如文件系统、组织架构或导航菜单,"手机端js tree"成为了一种实用的解决方案。这个技术基于JavaScript,专为智能手机和平板电脑等移动端设备设计,提供了可自定义的树形...
SPeedtree 7.14 for Unity是一款专为Unity引擎设计的高级植被渲染插件,它为游戏开发者提供了强大的自然环境构建工具。在Unity这个广泛使用的跨平台游戏开发框架中,SPeedtree能够帮助设计师们创建出栩栩如生、细节...
在Element UI库中,`el-tree` 是一个强大的组件,用于构建可交互的树形结构数据展示。在实际开发中,我们经常需要处理用户选择的节点,并可能需要独立展示这些选中节点,甚至允许用户在独立的树结构中进行删除操作。...
**Ajax Tree技术详解** 在网页开发中,树形结构(Tree)是一种常见的数据展示方式,尤其在管理和组织层级数据时非常实用。Ajax Tree是利用Ajax技术动态加载和更新树节点,提供用户友好的交互体验。它允许用户在不...
Excel中的TreePlan是一款强大的建模插件,专用于创建和分析决策树模型。在商业智能、项目管理和风险管理等领域,决策树是一种常用的分析工具,它通过图形化的方式展示各种可能的决策路径及其结果,帮助用户在不确定...
【EasyTree的使用教程】 EasyTree 是一个轻量级的前端组件,专用于构建和展示树型结构数据。它在Web应用中广泛用于组织和管理层次化的信息,如目录结构、组织架构或权限管理等。这个教程将详细介绍如何使用经过修改...
**jsTree:构建前端树形结构的利器** jsTree 是一个强大的 JavaScript 库,专用于在 Web 页面上创建交互式的树形结构。它基于纯 JavaScript 编写,无需依赖其他库,因此对于初学者和有经验的开发者来说,都是一个...
`Tree` 命令是 Windows 操作系统中一个实用的 DOS 命令,它允许用户以图形化的树状结构来查看指定驱动器或路径的文件夹结构。这种直观的展示方式对于理解和管理文件系统非常有帮助。下面将详细解释 `Tree` 命令的...
### KD-Tree基本教程知识点概览 #### 一、引言与背景介绍 - **教程来源**:本教程来源于Andrew W. Moore博士论文的一部分——《Efficient Memory-based Learning for Robot Control》,该章节专用于KD-Tree及其在...
i-Tree的五大核心产品包括:i-Tree Eco、i-Tree Streets、i-Tree Hydro、i-Tree Vue和i-Tree Species Selector。 1. i-Tree Eco:它能提供整个城市森林的概况分析,通过使用来自社区随机分布样区的现场数据和当地每...
《TableTree:构建表格树形结构的实现与应用》 在数据展示中,有时我们需要将层级关系的数据以表格的形式呈现,这时,表格树形结构(TableTree)就显得尤为重要。它将传统二维表格与树状结构相结合,既保留了表格的...
JavaScript Tree是一种交互式的前端UI组件,它以树形结构展示数据,常用于网站或应用程序的导航、目录组织或数据层级展示。"Checkbox Tree"是这种树结构的一个扩展,它在每个节点上添加了复选框,允许用户进行多选...