هژںو–‡هœ°ه€ï¼ڑhttp://www.cnblogs.com/weidagang2046/archive/2011/06/04/2063696.html
cat todd.log | grep programming | sort -r
çگ†è§£HTTPه¹‚ç‰و€§
هں؛ن؛ژHTTPهچڈè®®çڑ„Web APIوک¯و—¶ن¸‹وœ€ن¸؛وµپè،Œçڑ„ن¸€ç§چهˆ†ه¸ƒه¼ڈوœچهٹ،وڈگن¾›و–¹ه¼ڈم€‚و— è®؛وک¯هœ¨ه¤§ه‹ن؛’èپ”网ه؛”用è؟کوک¯ن¼پن¸ڑç؛§و¶و„ن¸ï¼Œوˆ‘ن»¬éƒ½è§پهˆ°ن؛†è¶ٹو¥è¶ٹه¤ڑçڑ„SOAوˆ–RESTfulçڑ„Web APIم€‚ن¸؛ن»€ن¹ˆWeb APIه¦‚و¤وµپè،Œه‘¢ï¼ںوˆ‘认ن¸؛ه¾ˆه¤§ç¨‹ه؛¦ن¸ٹه؛”ه½’هٹںن؛ژ简هچ•وœ‰و•ˆçڑ„HTTPهچڈè®®م€‚HTTPهچڈè®®وک¯ن¸€ç§چهˆ†ه¸ƒه¼ڈçڑ„é¢هگ‘资و؛گçڑ„网络ه؛”用ه±‚هچڈ议,و— è®؛وک¯وœچهٹ،ه™¨ç«¯وڈگن¾›Webوœچهٹ،,è؟کوک¯ه®¢وˆ·ç«¯و¶ˆè´¹Webوœچهٹ،都éه¸¸ç®€هچ•م€‚ه†چهٹ ن¸ٹوµڈ览ه™¨م€پJavascriptم€پAJAXم€پJSONن»¥هڈٹHTML5ç‰وٹ€وœ¯ه’Œه·¥ه…·çڑ„هڈ‘ه±•ï¼Œن؛’èپ”网ه؛”用و¶و„设è®،è،¨çژ°ه‡؛ن؛†ن»ژن¼ ç»ںçڑ„PHPم€پJSPم€پASP.NETç‰وœچهٹ،ه™¨ç«¯هٹ¨و€پ网é،µهگ‘Web API + RIA(ه¯Œن؛’èپ”网ه؛”用)è؟‡و¸،çڑ„趋هٹ؟م€‚Web APIن¸“و³¨ن؛ژوڈگن¾›ن¸ڑهٹ،وœچهٹ،,RIAن¸“و³¨ن؛ژ用وˆ·ç•Œé¢ه’Œن؛¤ن؛’设è®،,ن»ژو¤ن¸¤ن¸ھ领هںںçڑ„هˆ†ه·¥و›´هٹ وکژو™°م€‚هœ¨è؟™ç§چ趋هٹ؟ن¸‹ï¼ŒWeb API设è®،ه°†وˆگن¸؛وœچهٹ،ه™¨ç«¯ç¨‹ه؛ڈه‘کçڑ„ه؟…ن؟®è¯¾م€‚然而,و£ه¦‚简هچ•çڑ„Javaè¯è¨€ه¹¶ن¸چو„ڈه‘³ç€é«کè´¨é‡ڈçڑ„Java程ه؛ڈ,简هچ•çڑ„HTTPهچڈè®®ن¹ںن¸چو„ڈه‘³ç€é«کè´¨é‡ڈçڑ„Web APIم€‚è¦پوƒ³è®¾è®،ه‡؛é«کè´¨é‡ڈçڑ„Web API,è؟ک需è¦پو·±ه…¥çگ†è§£هˆ†ه¸ƒه¼ڈç³»ç»ںهڈٹHTTPهچڈè®®çڑ„特و€§م€‚
ه¹‚ç‰و€§ه®ڑن¹‰
وœ¬و–‡و‰€è¦پوژ¢è®¨çڑ„و£وک¯HTTPهچڈè®®و¶‰هڈٹهˆ°çڑ„ن¸€ç§چé‡چè¦پو€§è´¨ï¼ڑه¹‚ç‰و€§(Idempotence)م€‚هœ¨HTTP/1.1规范ن¸ه¹‚ç‰و€§çڑ„ه®ڑن¹‰وک¯ï¼ڑ
Methods can also have the property of "idempotence" in that (aside from error or expiration issues) the side-effects of N > 0 identical requests is the same as for a single request.
ن»ژه®ڑن¹‰ن¸ٹ看,HTTPو–¹و³•çڑ„ه¹‚ç‰و€§وک¯وŒ‡ن¸€و¬،ه’Œه¤ڑو¬،请و±‚وںگن¸€ن¸ھ资و؛گه؛”该ه…·وœ‰هگŒو ·çڑ„ه‰¯ن½œç”¨م€‚ه¹‚ç‰و€§ه±ن؛ژè¯ن¹‰èŒƒç•´ï¼Œو£ه¦‚编译ه™¨هڈھ能ه¸®هٹ©و£€وں¥è¯و³•é”™è¯¯ن¸€و ·ï¼ŒHTTP规范ن¹ںو²،وœ‰هٹو³•é€ڑè؟‡و¶ˆوپ¯و ¼ه¼ڈç‰è¯و³•و‰‹و®µو¥ه®ڑن¹‰ه®ƒï¼Œè؟™هڈ¯èƒ½وک¯ه®ƒن¸چه¤ھهڈ—هˆ°é‡چ视çڑ„هژںه› ن¹‹ن¸€م€‚ن½†ه®é™…ن¸ٹ,ه¹‚ç‰و€§وک¯هˆ†ه¸ƒه¼ڈç³»ç»ں设è®،ن¸هچپهˆ†é‡چè¦پçڑ„و¦‚ه؟µï¼Œè€ŒHTTPçڑ„هˆ†ه¸ƒه¼ڈوœ¬è´¨ن¹ںه†³ه®ڑن؛†ه®ƒهœ¨HTTPن¸ه…·وœ‰é‡چè¦پهœ°ن½چم€‚
هˆ†ه¸ƒه¼ڈن؛‹هٹ، vs ه¹‚ç‰è®¾è®،
ن¸؛ن»€ن¹ˆéœ€è¦په¹‚ç‰و€§ه‘¢ï¼ںوˆ‘ن»¬ه…ˆن»ژن¸€ن¸ھن¾‹هگ说起,هپ‡è®¾وœ‰ن¸€ن¸ھن»ژè´¦وˆ·هڈ–é’±çڑ„è؟œç¨‹API(هڈ¯ن»¥وک¯HTTPçڑ„,ن¹ںهڈ¯ن»¥ن¸چوک¯ï¼‰ï¼Œوˆ‘ن»¬وڑ‚و—¶ç”¨ç±»ه‡½و•°çڑ„و–¹ه¼ڈè®°ن¸؛ï¼ڑ
bool withdraw(account_id, amount)
withdrawçڑ„è¯ن¹‰وک¯ن»ژaccount_idه¯¹ه؛”çڑ„è´¦وˆ·ن¸و‰£é™¤amountو•°é¢çڑ„钱;ه¦‚وœو‰£é™¤وˆگهٹںهˆ™è؟”ه›true,账وˆ·ن½™é¢ه‡ڈه°‘amountï¼›ه¦‚وœو‰£é™¤ه¤±è´¥هˆ™è؟”ه›false,账وˆ·ن½™é¢ن¸چهڈکم€‚ه€¼ه¾—و³¨و„ڈçڑ„وک¯ï¼ڑه’Œوœ¬هœ°çژ¯ه¢ƒç›¸و¯”,وˆ‘ن»¬ن¸چ能轻وک“هپ‡è®¾هˆ†ه¸ƒه¼ڈçژ¯ه¢ƒçڑ„هڈ¯é و€§م€‚ن¸€ç§چه…¸ه‹çڑ„وƒ…ه†µوک¯withdraw请و±‚ه·²ç»ڈ被وœچهٹ،ه™¨ç«¯و£ç،®ه¤„çگ†ï¼Œن½†وœچهٹ،ه™¨ç«¯çڑ„è؟”ه›ç»“وœç”±ن؛ژ网络ç‰هژںه› 被وژ‰ن¸¢ن؛†ï¼Œه¯¼è‡´ه®¢وˆ·ç«¯و— و³•ه¾—çں¥ه¤„çگ†ç»“وœم€‚ه¦‚وœوک¯هœ¨ç½‘é،µن¸ٹ,ن¸€ن؛›ن¸چوپ°ه½“çڑ„设è®،هڈ¯èƒ½ن¼ڑن½؟用وˆ·è®¤ن¸؛ن¸ٹن¸€و¬،و“چن½œه¤±è´¥ن؛†ï¼Œç„¶هگژهˆ·و–°é،µé¢ï¼Œè؟™ه°±ه¯¼è‡´ن؛†withdraw被调用ن¸¤و¬،,账وˆ·ن¹ں被ه¤ڑو‰£ن؛†ن¸€و¬،é’±م€‚ه¦‚ه›¾1و‰€ç¤؛ï¼ڑ
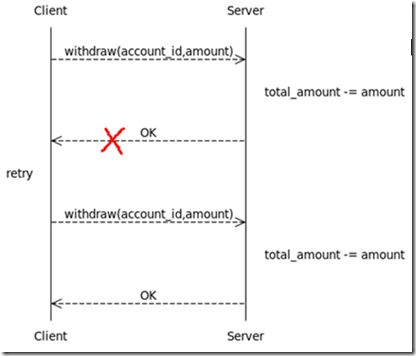
è؟™ن¸ھé—®é¢کçڑ„解ه†³و–¹و،ˆن¸€وک¯é‡‡ç”¨هˆ†ه¸ƒه¼ڈن؛‹هٹ،,é€ڑè؟‡ه¼•ه…¥و”¯وŒپهˆ†ه¸ƒه¼ڈن؛‹هٹ،çڑ„ن¸é—´ن»¶و¥ن؟è¯پwithdrawهٹں能çڑ„ن؛‹هٹ،و€§م€‚هˆ†ه¸ƒه¼ڈن؛‹هٹ،çڑ„ن¼ک点وک¯ه¯¹ن؛ژ调用者ه¾ˆç®€هچ•ï¼Œه¤چو‚و€§éƒ½ن؛¤ç»™ن؛†ن¸é—´ن»¶و¥ç®،çگ†م€‚ç¼؛点هˆ™وک¯ن¸€و–¹é¢و¶و„ه¤ھé‡چé‡ڈç؛§ï¼Œه®¹وک“被绑هœ¨ç‰¹ه®ڑçڑ„ن¸é—´ن»¶ن¸ٹ,ن¸چهˆ©ن؛ژه¼‚و„ç³»ç»ںçڑ„集وˆگï¼›هڈ¦ن¸€و–¹é¢هˆ†ه¸ƒه¼ڈن؛‹هٹ،虽然能ن؟è¯پن؛‹هٹ،çڑ„ACIDو€§è´¨ï¼Œè€Œن½†هچ´و— و³•وڈگن¾›و€§èƒ½ه’Œهڈ¯ç”¨و€§çڑ„ن؟è¯پم€‚
هڈ¦ن¸€ç§چو›´è½»é‡ڈç؛§çڑ„解ه†³و–¹و،ˆوک¯ه¹‚ç‰è®¾è®،م€‚وˆ‘ن»¬هڈ¯ن»¥é€ڑè؟‡ن¸€ن؛›وٹ€ه·§وٹٹwithdrawهڈکوˆگه¹‚ç‰çڑ„,و¯”ه¦‚ï¼ڑ
int create_ticket()
bool idempotent_withdraw(ticket_id, account_id, amount)
create_ticketçڑ„è¯ن¹‰وک¯èژ·هڈ–ن¸€ن¸ھوœچهٹ،ه™¨ç«¯ç”ںوˆگçڑ„ه”¯ن¸€çڑ„ه¤„çگ†هڈ·ticket_id,ه®ƒه°†ç”¨ن؛ژو ‡è¯†هگژç»çڑ„و“چن½œم€‚idempotent_withdrawه’Œwithdrawçڑ„هŒ؛هˆ«هœ¨ن؛ژه…³èپ”ن؛†ن¸€ن¸ھticket_id,ن¸€ن¸ھticket_idè،¨ç¤؛çڑ„و“چن½œè‡³ه¤ڑهڈھن¼ڑ被ه¤„çگ†ن¸€و¬،,و¯ڈو¬،调用都ه°†è؟”ه›ç¬¬ن¸€و¬،调用و—¶çڑ„ه¤„çگ†ç»“وœم€‚è؟™و ·ï¼Œidempotent_withdrawه°±ç¬¦هگˆه¹‚ç‰و€§ن؛†ï¼Œه®¢وˆ·ç«¯ه°±هڈ¯ن»¥و”¾ه؟ƒهœ°ه¤ڑو¬،调用م€‚
هں؛ن؛ژه¹‚ç‰و€§çڑ„解ه†³و–¹و،ˆن¸ن¸€ن¸ھه®Œو•´çڑ„هڈ–é’±وµپ程被هˆ†è§£وˆگن؛†ن¸¤ن¸ھو¥éھ¤ï¼ڑ1.调用create_ticket()èژ·هڈ–ticket_idï¼›2.调用idempotent_withdraw(ticket_id, account_id, amount)م€‚虽然create_ticketن¸چوک¯ه¹‚ç‰çڑ„,ن½†هœ¨è؟™ç§چ设è®،ن¸‹ï¼Œه®ƒه¯¹ç³»ç»ںçٹ¶و€پçڑ„ه½±ه“چهڈ¯ن»¥ه؟½ç•¥ï¼Œهٹ ن¸ٹidempotent_withdrawوک¯ه¹‚ç‰çڑ„,و‰€ن»¥ن»»ن½•ن¸€و¥ç”±ن؛ژ网络ç‰هژںه› ه¤±è´¥وˆ–超و—¶ï¼Œه®¢وˆ·ç«¯éƒ½هڈ¯ن»¥é‡چ试,直هˆ°èژ·ه¾—结وœم€‚ه¦‚ه›¾2و‰€ç¤؛ï¼ڑ

ه’Œهˆ†ه¸ƒه¼ڈن؛‹هٹ،相و¯”,ه¹‚ç‰è®¾è®،çڑ„ن¼کهٹ؟هœ¨ن؛ژه®ƒçڑ„è½»é‡ڈç؛§ï¼Œه®¹وک“适ه؛”ه¼‚و„çژ¯ه¢ƒï¼Œن»¥هڈٹو€§èƒ½ه’Œهڈ¯ç”¨و€§و–¹é¢م€‚هœ¨وںگن؛›و€§èƒ½è¦پو±‚و¯”较é«کçڑ„ه؛”用,ه¹‚ç‰è®¾è®،ه¾€ه¾€وک¯ه”¯ن¸€çڑ„选و‹©م€‚
HTTPçڑ„ه¹‚ç‰و€§
HTTPهچڈè®®وœ¬è؛«وک¯ن¸€ç§چé¢هگ‘资و؛گçڑ„ه؛”用ه±‚هچڈ议,ن½†ه¯¹HTTPهچڈè®®çڑ„ن½؟用ه®é™…ن¸ٹهکهœ¨ç€ن¸¤ç§چن¸چهگŒçڑ„و–¹ه¼ڈï¼ڑن¸€ç§چوک¯RESTfulçڑ„,ه®ƒوٹٹHTTPه½“وˆگه؛”用ه±‚هچڈ议,و¯”较ه؟ ه®هœ°éپµه®ˆن؛†HTTPهچڈè®®çڑ„هگ„ç§چ规ه®ڑï¼›هڈ¦ن¸€ç§چوک¯SOAçڑ„,ه®ƒه¹¶و²،وœ‰ه®Œه…¨وٹٹHTTPه½“وˆگه؛”用ه±‚هچڈ议,而وک¯وٹٹHTTPهچڈè®®ن½œن¸؛ن؛†ن¼ 输ه±‚هچڈ议,然هگژهœ¨HTTPن¹‹ن¸ٹه»؛ç«‹ن؛†è‡ھه·±çڑ„ه؛”用ه±‚هچڈè®®م€‚وœ¬و–‡و‰€è®¨è®؛çڑ„HTTPه¹‚ç‰و€§ن¸»è¦پé’ˆه¯¹RESTfulé£ژو ¼çڑ„,ن¸چè؟‡و£ه¦‚ن¸ٹن¸€èٹ‚و‰€çœ‹هˆ°çڑ„é‚£و ·ï¼Œه¹‚ç‰و€§ه¹¶ن¸چه±ن؛ژ特ه®ڑçڑ„هچڈ议,ه®ƒوک¯هˆ†ه¸ƒه¼ڈç³»ç»ںçڑ„ن¸€ç§چ特و€§ï¼›و‰€ن»¥ï¼Œن¸چè®؛وک¯SOAè؟کوک¯RESTfulçڑ„Web API设è®،都ه؛”该考虑ه¹‚ç‰و€§م€‚ن¸‹é¢ه°†ن»‹ç»چHTTP GETم€پDELETEم€پPUTم€پPOSTه››ç§چن¸»è¦پو–¹و³•çڑ„è¯ن¹‰ه’Œه¹‚ç‰و€§م€‚
HTTP GETو–¹و³•ç”¨ن؛ژèژ·هڈ–资و؛گ,ن¸چه؛”وœ‰ه‰¯ن½œç”¨ï¼Œو‰€ن»¥وک¯ه¹‚ç‰çڑ„م€‚و¯”ه¦‚ï¼ڑGET http://www.bank.com/account/123456,ن¸چن¼ڑو”¹هڈک资و؛گçڑ„çٹ¶و€پ,ن¸چè®؛调用ن¸€و¬،è؟کوک¯Nو¬،都و²،وœ‰ه‰¯ن½œç”¨م€‚请و³¨و„ڈ,è؟™é‡Œه¼؛è°ƒçڑ„وک¯ن¸€و¬،ه’ŒNو¬،ه…·وœ‰ç›¸هگŒçڑ„ه‰¯ن½œç”¨ï¼Œè€Œن¸چوک¯و¯ڈو¬،GETçڑ„结وœç›¸هگŒم€‚GET http://www.news.com/latest-newsè؟™ن¸ھHTTP请و±‚هڈ¯èƒ½ن¼ڑو¯ڈو¬،ه¾—هˆ°ن¸چهگŒçڑ„结وœï¼Œن½†ه®ƒوœ¬è؛«ه¹¶و²،وœ‰ن؛§ç”ںن»»ن½•ه‰¯ن½œç”¨ï¼Œه› 而وک¯و»،足ه¹‚ç‰و€§çڑ„م€‚
HTTP DELETEو–¹و³•ç”¨ن؛ژهˆ 除资و؛گ,وœ‰ه‰¯ن½œç”¨ï¼Œن½†ه®ƒه؛”该و»،足ه¹‚ç‰و€§م€‚و¯”ه¦‚ï¼ڑDELETE http://www.forum.com/article/4231,调用ن¸€و¬،ه’ŒNو¬،ه¯¹ç³»ç»ںن؛§ç”ںçڑ„ه‰¯ن½œç”¨وک¯ç›¸هگŒçڑ„,هچ³هˆ وژ‰idن¸؛4231çڑ„ه¸–هگï¼›ه› و¤ï¼Œè°ƒç”¨è€…هڈ¯ن»¥ه¤ڑو¬،调用وˆ–هˆ·و–°é،µé¢è€Œن¸چه؟…و‹…ه؟ƒه¼•èµ·é”™è¯¯م€‚
و¯”较ه®¹وک“و··و·†çڑ„وک¯HTTP POSTه’ŒPUTم€‚POSTه’ŒPUTçڑ„هŒ؛هˆ«ه®¹وک“被简هچ•هœ°è¯¯è®¤ن¸؛“POSTè،¨ç¤؛هˆ›ه»؛资و؛گ,PUTè،¨ç¤؛و›´و–°èµ„و؛گâ€ï¼›è€Œه®é™…ن¸ٹ,ن؛Œè€…ه‡هڈ¯ç”¨ن؛ژهˆ›ه»؛资و؛گ,و›´ن¸؛وœ¬è´¨çڑ„ه·®هˆ«وک¯هœ¨ه¹‚ç‰و€§و–¹é¢م€‚هœ¨HTTP规范ن¸ه¯¹POSTه’ŒPUTوک¯è؟™و ·ه®ڑن¹‰çڑ„ï¼ڑ
The POST method is used to request that the origin server accept the entity enclosed in the request as a new subordinate of the resource identified by the Request-URI in the Request-Line. ...... If a resource has been created on the origin server, the response SHOULD be 201 (Created) and contain an entity which describes the status of the request and refers to the new resource, and a Location header.
The PUT method requests that the enclosed entity be stored under the supplied Request-URI. If the Request-URI refers to an already existing resource, the enclosed entity SHOULD be considered as a modified version of the one residing on the origin server. If the Request-URI does not point to an existing resource, and that URI is capable of being defined as a new resource by the requesting user agent, the origin server can create the resource with that URI.
POSTو‰€ه¯¹ه؛”çڑ„URIه¹¶éهˆ›ه»؛çڑ„资و؛گوœ¬è؛«ï¼Œè€Œوک¯èµ„و؛گçڑ„وژ¥و”¶è€…م€‚و¯”ه¦‚ï¼ڑPOST http://www.forum.com/articlesçڑ„è¯ن¹‰وک¯هœ¨http://www.forum.com/articlesن¸‹هˆ›ه»؛ن¸€ç¯‡ه¸–هگ,HTTPه“چه؛”ن¸ه؛”هŒ…هگ«ه¸–هگçڑ„هˆ›ه»؛çٹ¶و€پن»¥هڈٹه¸–هگçڑ„URIم€‚ن¸¤و¬،相هگŒçڑ„POST请و±‚ن¼ڑهœ¨وœچهٹ،ه™¨ç«¯هˆ›ه»؛ن¸¤ن»½èµ„و؛گ,ه®ƒن»¬ه…·وœ‰ن¸چهگŒçڑ„URIï¼›و‰€ن»¥ï¼ŒPOSTو–¹و³•ن¸چه…·ه¤‡ه¹‚ç‰و€§م€‚而PUTو‰€ه¯¹ه؛”çڑ„URIوک¯è¦پهˆ›ه»؛وˆ–و›´و–°çڑ„资و؛گوœ¬è؛«م€‚و¯”ه¦‚ï¼ڑPUT http://www.forum/articles/4231çڑ„è¯ن¹‰وک¯هˆ›ه»؛وˆ–و›´و–°IDن¸؛4231çڑ„ه¸–هگم€‚ه¯¹هگŒن¸€URIè؟›è،Œه¤ڑو¬،PUTçڑ„ه‰¯ن½œç”¨ه’Œن¸€و¬،PUTوک¯ç›¸هگŒçڑ„ï¼›ه› و¤ï¼ŒPUTو–¹و³•ه…·وœ‰ه¹‚ç‰و€§م€‚
هœ¨ن»‹ç»چن؛†ه‡ ç§چو“چن½œçڑ„è¯ن¹‰ه’Œه¹‚ç‰و€§ن¹‹هگژ,وˆ‘ن»¬و¥çœ‹çœ‹ه¦‚ن½•é€ڑè؟‡Web APIçڑ„ه½¢ه¼ڈه®çژ°ه‰چé¢و‰€وڈگهˆ°çڑ„هڈ–و¬¾هٹں能م€‚ه¾ˆç®€هچ•ï¼Œç”¨POST /ticketsو¥ه®çژ°create_ticket;用PUT /accounts/account_id/ticket_id&amount=xxxو¥ه®çژ°idempotent_withdrawم€‚ه€¼ه¾—و³¨و„ڈçڑ„وک¯ن¸¥و ¼و¥è®²amountهڈ‚و•°ن¸چه؛”该ن½œن¸؛URIçڑ„ن¸€éƒ¨هˆ†ï¼Œçœںو£çڑ„URIه؛”该وک¯/accounts/account_id/ticket_id,而amountه؛”该و”¾هœ¨è¯·و±‚çڑ„bodyن¸م€‚è؟™ç§چو¨،ه¼ڈهڈ¯ن»¥ه؛”用ن؛ژه¾ˆه¤ڑهœ؛هگˆï¼Œو¯”ه¦‚ï¼ڑè®؛ه›ç½‘ç«™ن¸éک²و¢و„ڈه¤–çڑ„é‡چه¤چهڈ‘ه¸–م€‚
و€»ç»“
ن¸ٹé¢ç®€هچ•ن»‹ç»چن؛†ه¹‚ç‰و€§çڑ„و¦‚ه؟µï¼Œç”¨ه¹‚ç‰è®¾è®،هڈ–ن»£هˆ†ه¸ƒه¼ڈن؛‹هٹ،çڑ„و–¹و³•ï¼Œن»¥هڈٹHTTPن¸»è¦پو–¹و³•çڑ„è¯ن¹‰ه’Œه¹‚ç‰و€§ç‰¹ه¾پم€‚ه…¶ه®ï¼Œه¦‚وœè¦پè؟½و ¹و؛¯و؛گ,ه¹‚ç‰و€§وک¯و•°ه¦ن¸çڑ„ن¸€ن¸ھو¦‚ه؟µï¼Œè،¨è¾¾çڑ„وک¯Nو¬،هڈکوچ¢ن¸ژ1و¬،هڈکوچ¢çڑ„结وœç›¸هگŒï¼Œوœ‰ه…´è¶£çڑ„读者هڈ¯ن»¥ن»ژWikipediaن¸ٹè؟›ن¸€و¥ن؛†è§£م€‚
هڈ‚考
RFC 2616, Hypertext Transfer Protocol -- HTTP/1.1, Method Definitions
The Importance of Idempotence
stackoverflow - PUT vs POST in REST
هˆ†ن؛«هˆ°ï¼ڑ











相ه…³وژ¨èچگ
Alibaba_Java_Coding_Guidelines-2.2.3.0x
م€گABBوœ؛ه™¨ن؛؛م€‘-IRB460وœ؛ه™¨ن؛؛ç»´وٹ¤ن؟،وپ¯V1.pdf
ه†…ه®¹و¦‚è¦پï¼ڑوœ¬و–‡è¯¦ç»†ن»‹ç»چن؛†و–°èƒ½و؛گو±½è½¦VCU(车辆وژ§هˆ¶هچ•ه…ƒï¼‰وژ§هˆ¶ه™¨çڑ„ه¼€و؛گé،¹ç›®ï¼Œو¶µç›–ن»ژه؛”用ه±‚ن»£ç پهˆ°ه؛•ه±‚ن»£ç پم€پهژںçگ†ه›¾م€پPCB设è®،م€پé€ڑن؟،هچڈè®®هڈٹوژ§هˆ¶ç–ç•¥ç‰ه¤ڑن¸ھو–¹é¢م€‚ه؛”用ه±‚ن»£ç په±•ç¤؛ن؛†ه¦‚ن½•و ¹وچ®ç”µو± 电é‡ڈè°ƒو•´è½¦è¾†è،Œé©¶و¨،ه¼ڈ,ه؛•ه±‚ن»£ç پو¶‰هڈٹç،¬ن»¶é©±هٹ¨ه¦‚GPIOوژ§هˆ¶ه’ŒADC采و ·é…چç½®م€‚ç،¬ن»¶è®¾è®،部هˆ†هŒ…و‹¬è¯¦ç»†çڑ„هژںçگ†ه›¾ه’ŒPCBه¸ƒه±€ï¼Œç،®ن؟ç³»ç»ںçڑ„稳ه®ڑو€§ه’Œهڈ¯é و€§م€‚é€ڑن؟،هچڈ议采用CAN网络,ç،®ن؟و•°وچ®هڈ¯é ن¼ 输,وژ§هˆ¶ç–ç•¥هˆ™و¶µç›–ن؛†èƒ½é‡ڈه›و”¶م€پو‰çں©وژ§هˆ¶ç‰ه…³é”®وٹ€وœ¯م€‚ن¸°ه¯Œçڑ„و–‡و،£èµ„و–™ه’Œوµ‹è¯•ç”¨ن¾‹ن¸؛ه¼€هڈ‘ن؛؛ه‘کوڈگن¾›ن؛†ه®è´µçڑ„ه¦ن¹ ه’Œه¼€هڈ‘资و؛گم€‚ 适هگˆن؛؛群ï¼ڑو–°èƒ½و؛گو±½è½¦ه¼€هڈ‘ن؛؛ه‘کم€پç،¬ن»¶ه·¥ç¨‹ه¸ˆم€پهµŒه…¥ه¼ڈ软ن»¶ه·¥ç¨‹ه¸ˆم€په¦ç”ںهڈٹç ”ç©¶ن؛؛ه‘کم€‚ ن½؟用هœ؛و™¯هڈٹç›®و ‡ï¼ڑه¸®هٹ©ه¼€هڈ‘ن؛؛ه‘کو·±ه…¥ن؛†è§£و–°èƒ½و؛گو±½è½¦VCUوژ§هˆ¶ه™¨çڑ„ه·¥ن½œهژںçگ†ه’Œوٹ€وœ¯ç»†èٹ‚,هٹ é€ںé،¹ç›®ه¼€هڈ‘è؟›ç¨‹ï¼Œé™چن½ژه¼€هڈ‘éڑ¾ه؛¦م€‚و— è®؛وک¯هˆه¦è€…è؟کوک¯وœ‰ç»ڈéھŒçڑ„ن¸“ن¸ڑن؛؛ه£«ï¼Œéƒ½هڈ¯ن»¥ن»ژن¸هڈ—ç›ٹم€‚ ه…¶ن»–说وکژï¼ڑ该é،¹ç›®ن¸چن»…وڈگن¾›ن؛†ه®Œو•´çڑ„و؛گن»£ç په’Œç،¬ن»¶è®¾è®،و–‡ن»¶ï¼Œè؟کهŒ…و‹¬è¯¦ç»†çڑ„وµ‹è¯•ç”¨ن¾‹ه’Œو•…éڑœه¤„çگ†و–¹و،ˆï¼Œن½؟ه¾—VCUه¼€هڈ‘هڈکه¾—و›´هٹ é€ڈوکژه’Œهڈ¯ه¤چçژ°م€‚
详解DeepSeekçڑ„هچپن¸ھه®‰ه…¨é—®é¢ک.pdf
م€ٹ网络ن¼ و’وٹ€وœ¯ن¸ژه®هٹ،م€‹ç¬¬10ç« -وڈ،هœ¨و‰‹ن¸çڑ„网络——移هٹ¨é€ڑن؟،ن¸ژو— ç؛؟网络وٹ€وœ¯.ppt
م€ٹè®،ç®—وœ؛ن¸“ن¸ڑ英è¯م€‹chapter9-Communication-by-Avatars.ppt
و€§èƒ½وµ‹è¯•ه·¥ه…·Xrunnerçڑ„ن½؟用و‰‹ه†Œ
ه†…ه®¹و¦‚è¦پï¼ڑوœ¬و–‡و·±ه…¥وژ¢è®¨ن؛†هں؛ن؛ژè‡ھوٹ—و‰°وژ§هˆ¶ï¼ˆADRC)çڑ„و°¸ç£پهگŒو¥ç”µوœ؛(PMSM)çں¢é‡ڈوژ§هˆ¶è°ƒé€ںç³»ç»ںçڑ„ن»؟çœںو–¹و³•هڈٹه…¶ن¼کهٹ؟م€‚首ه…ˆن»‹ç»چن؛†و¨،ه‹وگه»؛,هŒ…و‹¬DCç›´وµپ电هژ‹و؛گم€پن¸‰ç›¸é€†هڈکه™¨م€پو°¸ç£پهگŒو¥ç”µوœ؛م€پ采و ·و¨،ه—م€پClarkم€پParkم€پIparkن»¥هڈٹSVPWMç‰ه…³é”®ç»„ن»¶م€‚وژ¥ç€è¯¦ç»†è§£وگن؛†ADRCهœ¨ç”µوµپçژ¯ه’Œè½¬é€ںçژ¯ن¸çڑ„ه؛”用,ه±•ç¤؛ن؛†ه…¶é€ڑè؟‡و‰©ه¼ çٹ¶و€پ观وµ‹ه™¨ï¼ˆESO)ه®çژ°çڑ„é«کç²¾ه؛¦و‰°هٹ¨è§‚وµ‹ن¸ژè،¥هپ؟وœ؛هˆ¶م€‚و–‡ن¸è؟کوڈگن¾›ن؛†éƒ¨هˆ†MATLABن»£ç پç¤؛ن¾‹ï¼Œه¦‚SVPWMو¨،ه—ه’ŒADRCوژ§هˆ¶ه™¨çڑ„ه…·ن½“ه®çژ°م€‚ن»؟çœں结وœوک¾ç¤؛,ADRC相و¯”ن¼ ç»ںPIوژ§هˆ¶ه™¨ï¼Œهœ¨çھپهٹ è´ںè½½و—¶è،¨çژ°ه‡؛و›´ه¥½çڑ„稳ه®ڑو€§ه’Œو›´ه؟«çڑ„ه“چه؛”é€ںه؛¦ï¼Œن¸”ن¸چهکهœ¨ç§¯هˆ†é¥±ه’Œé—®é¢کم€‚و¤ه¤–,و–‡ç« 讨è®؛ن؛†ن¸€ن؛›ه®é™…ه؛”用ن¸çڑ„و³¨و„ڈن؛‹é،¹ه’Œوٹ€وœ¯وŒ‘وˆکم€‚ 适هگˆن؛؛群ï¼ڑن»ژن؛‹ç”µوœ؛وژ§هˆ¶é¢†هںںçڑ„ç ”ç©¶ن؛؛ه‘کم€په·¥ç¨‹ه¸ˆهڈٹé«کو ،相ه…³ن¸“ن¸ڑه¸ˆç”ںم€‚ ن½؟用هœ؛و™¯هڈٹç›®و ‡ï¼ڑ适用ن؛ژه¸Œوœ›و·±ه…¥ن؛†è§£ه’ŒوژŒوڈ،çژ°ن»£ه…ˆè؟›ç”µوœ؛وژ§هˆ¶وٹ€وœ¯çڑ„ç ”ç©¶ن؛؛ه‘که’Œه·¥ç¨‹ه¸ˆم€‚ç›®و ‡وک¯é€ڑè؟‡ن»؟çœںه¹³هڈ°éھŒè¯پADRCçڑ„وœ‰و•ˆو€§ï¼Œه¹¶ن¸؛ه®é™…ه·¥ç¨‹é،¹ç›®وڈگن¾›çگ†è®؛و”¯وŒپه’Œوٹ€وœ¯وŒ‡ه¯¼م€‚ ه…¶ن»–说وکژï¼ڑه°½ç®،ADRCه…·وœ‰è¯¸ه¤ڑن¼ک点,ن½†هœ¨ه®é™…ه؛”用ن¸ن»چ需و³¨و„ڈهڈ‚و•°é€‰و‹©ه’Œç،¬ن»¶و،ن»¶é™گهˆ¶ç‰é—®é¢کم€‚
م€ٹ网络设ه¤‡ه®‰è£…ن¸ژ调试(é”گوچ·ç‰ˆ)م€‹é،¹ç›®1-é…چç½®ن؛¤وچ¢وœ؛设ه¤‡-ن¼کهŒ–网络ن¼ 输.pptx
ه†…ه®¹و¦‚è¦پï¼ڑوœ¬و–‡è¯¦ç»†ن»‹ç»چن؛†ه¦‚ن½•ن½؟用Fortranè¯è¨€هœ¨ABAQUSن¸ه¼€هڈ‘UMAT(用وˆ·وگو–™هگ程ه؛ڈ)ه’ŒVUMAT(وک¾ه¼ڈ用وˆ·وگو–™هگ程ه؛ڈ),ن»¥ه®çژ°وگو–™وچںن¼¤و–裂ه¼¹ه،‘و€§çڑ„è‡ھه®ڑن¹‰ه»؛و¨،م€‚و–‡ç« 首ه…ˆéکگè؟°ن؛†وگو–™وچںن¼¤و–裂ه¼¹ه،‘و€§çڑ„é‡چè¦پو€§ه’Œه؛”用هœ؛و™¯ï¼Œه¼؛è°ƒن؛†è‡ھه®ڑن¹‰وگو–™هگ程ه؛ڈهœ¨ه¤„çگ†ه¤چو‚وگو–™è،Œن¸؛و–¹é¢çڑ„ن¼کهٹ؟م€‚وژ¥ç€ï¼Œهˆ†هˆ«ه±•ç¤؛ن؛†UMATه’ŒVUMATçڑ„هں؛وœ¬ن»£ç پ结و„هڈٹه…¶و ¸ه؟ƒè®،ç®—و¥éھ¤ï¼Œه¦‚وگو–™هڈ‚و•°è¯»هڈ–م€په¼¹و€§هˆڑه؛¦çں©éکµهˆه§‹هŒ–م€په،‘و€§ه؛”هڈکه¢é‡ڈè®،ç®—ن»¥هڈٹه؛”هٹ›و›´و–°ç‰م€‚و¤ه¤–,è؟ک讨è®؛ن؛†DISPو¨،ه‹çڑ„ه؛”用,وڈگن¾›ن؛†ه…·ن½“çڑ„وچںن¼¤و¼”هŒ–ه’Œه؛”هٹ›وٹکه‡ڈو–¹و³•ï¼Œه¹¶هˆ†ن؛«ن؛†ن¸€ن؛›ه®ç”¨çڑ„调试وٹ€ه·§ه’Œو³¨و„ڈن؛‹é،¹م€‚ 适هگˆن؛؛群ï¼ڑه…·ه¤‡ن¸€ه®ڑABAQUSن½؟用ç»ڈéھŒه’ŒFortran编程هں؛ç،€çڑ„ç ”ç©¶ن؛؛ه‘که’Œوٹ€وœ¯ن؛؛ه‘ک,ه°¤ه…¶وک¯ن»ژن؛‹وگو–™هٹ›ه¦م€پ结و„ه·¥ç¨‹ç‰é¢†هںںçڑ„ه·¥ن½œن؛؛ه£«م€‚ ن½؟用هœ؛و™¯هڈٹç›®و ‡ï¼ڑ适用ن؛ژ需è¦په¯¹ç‰¹ه®ڑوگو–™è؟›è،Œç²¾ç،®ه»؛و¨،çڑ„ه·¥ç¨‹é،¹ç›®ï¼Œه¦‚èˆھç©؛èˆھه¤©م€پهœںوœ¨ه»؛ç‘ç‰م€‚é€ڑè؟‡è‡ھه®ڑن¹‰UMATه’ŒVUMATهگ程ه؛ڈ,能ه¤ںو›´ه¥½هœ°و¨،و‹ںوگو–™هœ¨ه¤چو‚è½½èچ·و،ن»¶ن¸‹çڑ„وچںن¼¤و¼”هŒ–ن¸ژو–裂è؟‡ç¨‹ï¼Œوڈگé«ک结و„ه®‰ه…¨و€§ه’Œهڈ¯é و€§è¯„ن¼°çڑ„ه‡†ç،®و€§م€‚ ه…¶ن»–说وکژï¼ڑو–‡ن¸ن¸چن»…وڈگن¾›ن؛†è¯¦ç»†çڑ„ن»£ç پç¤؛ن¾‹ï¼Œè؟کهˆ†ن؛«ن؛†è®¸ه¤ڑه®è·µç»ڈéھŒï¼Œه¸®هٹ©ه¼€هڈ‘者éپ؟ه…چه¸¸è§پ错误ه¹¶ن¼کهŒ–و€§èƒ½م€‚هگŒو—¶وڈگ醒读者ه…³و³¨وگو–™هڈ‚و•°çڑ„و£ç،®é…چç½®م€پé›…هڈ¯و¯”çں©éکµçڑ„ه¯¹ç§°و€§ç‰é—®é¢ک,ç،®ن؟è®،算稳ه®ڑهڈ¯é م€‚
V1_3_example.ipynb
ه®‰ه·وœ؛ه™¨ن؛؛DX100و“چن½œè¦پ领ن¹¦ é€ڑ用-وگ¬è؟گ用途-E.0.pdf
è؟™ن¸ھوک¯ه®Œو•´و؛گç پ SpringBoot + vue ه®çژ° م€گjavaو¯•ن¸ڑ设è®،م€‘SpringBoot+Vueه›¾ن¹¦é¦†(ه›¾ن¹¦ه€ںéک…)ç®،çگ†ç³»ç»ں و؛گç پ+sqlè„ڑوœ¬+è®؛و–‡ ه®Œو•´ç‰ˆ و•°وچ®ه؛“وک¯mysql éڑڈç€ç¤¾ن¼ڑçڑ„هڈ‘ه±•ï¼Œè®،ç®—وœ؛çڑ„ن¼کهٹ؟ه’Œو™®هڈٹن½؟ه¾—éک؟هچڑه›¾ن¹¦é¦†ç®،çگ†ç³»ç»ںçڑ„ه¼€هڈ‘وˆگن¸؛ه؟…需م€‚éک؟هچڑه›¾ن¹¦é¦†ç®،çگ†ç³»ç»ںن¸»è¦پوک¯ه€ںهٹ©è®،ç®—وœ؛,é€ڑè؟‡ه¯¹ه›¾ن¹¦ه€ںéک…ç‰ن؟،وپ¯è؟›è،Œç®،çگ†م€‚ه‡ڈه°‘ç®،çگ†ه‘کçڑ„ه·¥ن½œï¼Œن½œï¼ŒهگŒو—¶ن¹ںو–¹ن¾؟ه¹؟ه¤§ç”¨وˆ·ه¯¹و‰€éœ€ه›¾ن¹¦ه€ںéک…ن؟،وپ¯çڑ„هڈٹو—¶وں¥è¯¢ن»¥هڈٹç®،çگ†م€‚ éک؟هچڑه›¾ن¹¦é¦†ç®،çگ†ç³»ç»ںçڑ„ه¼€هڈ‘è؟‡ç¨‹ن¸ï¼Œé‡‡ç”¨B / Sو¶و„,ن¸»è¦پن½؟用Javaوٹ€وœ¯è؟›è،Œه¼€هڈ‘,结هگˆوœ€و–°وµپè،Œçڑ„springbootو،†و¶م€‚ن½؟用Mysqlو•°وچ®ه؛“ه’ŒEclipseه¼€هڈ‘çژ¯ه¢ƒم€‚该éک؟هچڑه›¾ن¹¦é¦†é¦†ç®،çگ†ç³»ç»ںçڑ„ه¼€هڈ‘è؟‡ç¨‹ن¸ï¼Œé‡‡ç”¨B / Sو¶و„,ن¸»è¦پن½؟用Javaوٹ€وœ¯è؟›è،Œه¼€هڈ‘,结هگˆوœ€و–°وµپè،Œçڑ„spriç®،çگ†ç³»ç»ںهŒ…و‹¬ç”¨وˆ·ه’Œç®،çگ†ه‘کم€‚ه…¶ن¸»è¦پهٹں能هŒ…و‹¬ç®،çگ†ه‘کï¼ڑ首é،µم€پن¸ھن؛؛ن¸ه؟ƒم€پ用وˆ·ç®،çگ†م€په›¾ن¹¦هˆ†ç±»ç®،çگ†م€په›¾ن¹¦ن؟،وپ¯ç®،çگ†م€په›¾ن¹¦ه€ںéک…ç®،çگ†م€په›¾ن¹¦ه½’è؟کç®،çگ†م€پç¼´ç؛³ç½ڑ金ç®،çگ†م€پ留言و؟ç®،çگ†م€پç³»هگŒو—¶ن¹ںو–¹ن¾؟ه¹؟ه¤§ç”¨وˆ·ه¯¹و‰€éœ€ه›¾ن¹¦ه€ںéک…ن؟،وپ¯çڑ„هڈٹو—¶وں¥è¯¢ن»¥هڈٹç®،çگ†م€‚ éک؟هچڑه›¾ن¹¦é¦†ç®،çگ†ç³»ç»ںçڑ„ه¼€هڈ‘è؟‡ç¨‹ن¸ï¼Œé‡‡ç”¨B / Sو¶و„,ن¸»è¦پن½؟用Javaوٹ€وœ¯è؟›è،Œه¼€هڈ‘,结هگˆوœ€و–°وµپè،Œçڑ„springbootو،†و¶م€‚ن½؟用Mysqlو•°وچ®ه؛“ه’ŒEclipseه¼€هڈ‘çژ¯ه¢ƒم€‚该éک؟هچڑه›¾ن¹¦é¦†ç®،çگ†ç³»ç»ںهŒ…و‹¬ç”¨وˆ·ه’Œç®،çگ†ه‘کم€‚ه…¶ن¸»è¦پهٹں能هŒ…و‹¬ç®،çگ†ه‘کï¼ڑ首é،µم€پن¸ھن؛؛ن¸ه؟ƒم€پ用وˆ·ç®،çگ†م€په›¾ن¹¦هˆ†ç±»ç®،çگ†م€په›¾ن¹¦ن؟،وپ¯ç®،çگ†م€په›¾ن¹¦ه€ںéک…ç®،çگ†م€په›¾ن¹¦ه½’è؟کç®،çگ†م€پç¼´ç؛³ç½ڑ金ç®،çگ†م€پ留言و؟ç®،çگ†م€پç³»ç»ںç®،çگ†ï¼Œç”¨وˆ·ï¼ڑ首é،µم€پن¸ھن؛؛ن¸ه؟ƒم€په›¾ن¹¦ه€ںéک…ç®،çگ†م€په›¾ن¹¦ه½’è؟کç®،çگ†م€پç¼´ç؛³ç½ڑ金ç®،çگ†م€پوˆ‘çڑ„و”¶è—ڈç®،çگ†ï¼Œه‰چهڈ°é¦–é،µï¼›é¦–é،µم€په›¾ن¹¦ن؟،وپ¯م€په…¬ه‘ٹن؟،وپ¯م€پ留言هڈچ馈م€پن¸ھن؛؛ن¸ه؟ƒم€پهگژهڈ°ç®،çگ†ç‰هٹں能م€‚ وœ¬è®؛و–‡ه¯¹éک؟هچڑه›¾ن¹¦é¦†ç®،çگ†ç³»ç»ںçڑ„هڈ‘ه±•èƒŒو™¯è؟›è،Œè¯¦ç»†çڑ„ن»‹ç»چ,ه¹¶ن¸”ه¯¹ç³»ç»ںه¼€هڈ‘وٹ€وœ¯è؟›è،Œن»‹ç»چ,然هگژه¯¹ç³»ç»ںè؟›è،Œéœ€و±‚هˆ†وگ,ه¯¹éک؟هچڑه›¾ن¹¦é¦†ç®،çگ†ç³»ç»ںن¸ڑهٹ،وµپ程م€پç³»ç»ں结و„ن»¥هڈٹو•°وچ®éƒ½è؟›è،Œè¯¦ç»†è¯´وکژم€‚用وˆ·هڈ¯و ¹وچ®ه…³é”®ه—è؟›è،Œوں¥و‰¾è‡ھه·±وƒ³è¦پçڑ„ن؟،وپ¯ç‰م€‚
ه†…ه®¹و¦‚è¦پï¼ڑوœ¬و–‡è¯¦ç»†ن»‹ç»چن؛†ن¸€ن¸ھهں؛ن؛ژYALMIPه’ŒMATLABçڑ„ه¾®ç”µç½‘ن¼کهŒ–è°ƒه؛¦و¨،ه‹ï¼Œو—¨هœ¨ه¸®هٹ©و–°و‰‹çگ†è§£ه’Œه؛”用ه¾®ç”µç½‘ن¼کهŒ–è°ƒه؛¦çڑ„هں؛وœ¬و¦‚ه؟µه’Œوٹ€وœ¯م€‚و¨،ه‹ç»¼هگˆè€ƒè™‘ن؛†è“„电و± ç®،çگ†م€په¸‚هœ؛è´ç”µه”®ç”µç؛¦وںن»¥هڈٹهٹںçژ‡ه¹³è،،ç‰ه› ç´ ï¼Œن»¥ه®çژ°ç³»ç»ںو€»è´¹ç”¨وœ€ن½ژن¸؛ç›®و ‡م€‚و–‡ن¸وڈگن¾›ن؛†è¯¦ç»†çڑ„MATLABن»£ç پç¤؛ن¾‹ï¼Œو¶µç›–هڈکé‡ڈه®ڑن¹‰م€پç؛¦وںو،ن»¶ه»؛ç«‹م€پç›®و ‡ه‡½و•°è®¾ه®ڑهڈٹن¼کهŒ–و±‚解è؟‡ç¨‹ï¼Œه¹¶é™„ه¸¦ن؛†è°ƒè¯•ه»؛è®®ه’Œهڈ¯è§†هŒ–و–¹و³•م€‚و¤ه¤–,è؟ک讨è®؛ن؛†ن¸€ن؛›ه¸¸è§پçڑ„错误هڈٹه…¶è§£ه†³هٹو³•ï¼Œه¦‚ه……و”¾ç”µن؛’و–¥ç؛¦وںم€پهٹںçژ‡ه¹³è،،ç؛¦وںç‰م€‚ 适هگˆن؛؛群ï¼ڑه¯¹ه¾®ç”µç½‘ن¼کهŒ–è°ƒه؛¦و„ںه…´è¶£çڑ„هˆه¦è€…,ه°¤ه…¶وک¯وœ‰ن¸€ه®ڑMATLABهں؛ç،€çڑ„ه¦ç”ںوˆ–ç ”ç©¶ن؛؛ه‘کم€‚ ن½؟用هœ؛و™¯هڈٹç›®و ‡ï¼ڑ适用ن؛ژه¸Œوœ›ه؟«é€ںوژŒوڈ،ه¾®ç”µç½‘ن¼کهŒ–è°ƒه؛¦هں؛وœ¬هژںçگ†çڑ„ه¦ن¹ 者,é€ڑè؟‡هٹ¨و‰‹ه®è·µهٹ و·±ه¯¹ç›¸ه…³çگ†è®؛çڑ„çگ†è§£م€‚ه…·ن½“ه؛”用هœ؛و™¯هŒ…و‹¬ن½†ن¸چé™گن؛ژï¼ڑه¦وœ¯ç ”究م€پ课程ن½œن¸ڑم€پن¸ھن؛؛ه…´è¶£é،¹ç›®ç‰م€‚ ه…¶ن»–说وکژï¼ڑ该و¨،ه‹ن¸چن»…وœ‰هٹ©ن؛ژçگ†è§£ه¾®ç”µç½‘çڑ„ه·¥ن½œوœ؛هˆ¶ï¼Œè؟کهڈ¯ن»¥ن¸؛è؟›ن¸€و¥وژ¢ç´¢ه¤چو‚çڑ„ه¾®ç”µç½‘ن¼کهŒ–é—®é¢که¥ ه®ڑهڑه®çڑ„هں؛ç،€م€‚
ه†…ه®¹و¦‚è¦پï¼ڑوœ¬و–‡è¯¦ç»†ن»‹ç»چن؛†ه¦‚ن½•هˆ©ç”¨MATLABوگه»؛هچ·ç§¯ç¥ç»ڈ网络(CNN),用ن؛ژه¤„çگ†ه…·وœ‰10ن¸ھ输ه…¥ç‰¹ه¾په’Œ3ن¸ھ输ه‡؛هڈکé‡ڈçڑ„و•°وچ®é¢„وµ‹ن»»هٹ،م€‚首ه…ˆè؟›è،Œو•°وچ®é¢„ه¤„çگ†ï¼ŒهŒ…و‹¬و•°وچ®è¯»هڈ–م€په½’ن¸€هŒ–ن»¥هڈٹè®ç»ƒé›†ه’Œوµ‹è¯•é›†çڑ„هˆ’هˆ†م€‚وژ¥ç€è®¾è®،ن؛†ن¸€ن¸ھهŒ…هگ«ه¤ڑن¸ھهچ·ç§¯ه±‚م€پو‰¹é‡ڈه½’ن¸€هŒ–ه±‚م€پReLUو؟€و´»ه‡½و•°ه±‚ه’Œه…¨è؟وژ¥ه±‚çڑ„网络و¶و„,ç،®ن؟能ه¤ںوœ‰و•ˆوڈگهڈ–特ه¾په¹¶ه®Œوˆگه¤ڑ输ه‡؛预وµ‹م€‚è®ç»ƒè؟‡ç¨‹ن¸é‡‡ç”¨Adamن¼کهŒ–ç®—و³•ï¼Œه¹¶è®¾ç½®ن؛†هگˆçگ†çڑ„超هڈ‚و•°ه¦‚وœ€ه¤§è؟ن»£و¬،و•°م€پو‰¹و¬،ه¤§ه°ڈه’Œهˆه§‹ه¦ن¹ çژ‡ç‰م€‚وœ€ç»ˆé€ڑè؟‡é¢„وµ‹ه’Œهڈچه½’ن¸€هŒ–و¥éھ¤ه¾—هˆ°و¨،ه‹و€§èƒ½è¯„ن»·وŒ‡و ‡MAEه’ŒRآ²ï¼Œه±•ç¤؛ن؛†è‰¯ه¥½çڑ„预وµ‹و•ˆوœم€‚ 适هگˆن؛؛群ï¼ڑه…·وœ‰ن¸€ه®ڑMATLAB编程هں؛ç،€ه’Œوٹ€وœ¯èƒŒو™¯çڑ„ç ”ç©¶ن؛؛ه‘کوˆ–ه·¥ç¨‹ه¸ˆï¼Œه°¤ه…¶وک¯é‚£ن؛›ن»ژن؛‹و•°وچ®هˆ†وگم€پوœ؛ه™¨ه¦ن¹ 领هںںçڑ„ن¸“ن¸ڑن؛؛ه£«م€‚ ن½؟用هœ؛و™¯هڈٹç›®و ‡ï¼ڑ适用ن؛ژ需è¦پ解ه†³ه¤ڑ输ه…¥ه¤ڑ输ه‡؛预وµ‹é—®é¢کçڑ„ه®é™…é،¹ç›®ن¸ï¼Œو¯”ه¦‚ه·¥ن¸ڑç”ںن؛§è؟‡ç¨‹ç›‘وژ§م€پ设ه¤‡و•…éڑœè¯ٹو–ç‰é¢†هںںم€‚ç›®çڑ„وک¯ه¸®هٹ©ç”¨وˆ·وژŒوڈ،ن½؟用MATLABه®çژ°CNNçڑ„و–¹و³•è®؛,ن»ژ而وڈگé«که·¥ن½œو•ˆçژ‡ه’Œè§£ه†³é—®é¢کçڑ„能هٹ›م€‚ ه…¶ن»–说وکژï¼ڑو–‡ن¸وڈگن¾›ن؛†ه®Œو•´çڑ„ن»£ç پ片و®µن¾›è¯»è€…هڈ‚考ه®è·µï¼ŒهگŒو—¶é’ˆه¯¹هڈ¯èƒ½ه‡؛çژ°çڑ„é—®é¢کç»™ه‡؛ن؛†ه®ç”¨و€§çڑ„ه»؛议,ه¦‚è°ƒو•´و‰¹é‡ڈه¤§ه°ڈم€پé™چن½ژه¦ن¹ çژ‡ç‰و–¹و³•و¥ه؛”ه¯¹è®ç»ƒن¸چ稳ه®ڑçڑ„وƒ…ه†µم€‚و¤ه¤–è؟کوڈگهˆ°ن؛†ن¸€ن؛›و”¹è؟›و–¹هگ‘,ن¾‹ه¦‚و”¹هڈکهچ·ç§¯و ¸ه°؛ه¯¸وˆ–者ه¼•ه…¥ç©؛و´هچ·ç§¯ن»¥ه¢ه¼؛و¨،ه‹è،¨çژ°م€‚
وœ؛ه™¨ن؛؛و¦‚è¦پ(ه¤–ه½¢ه›¾م€پç›®ه½•çڑ„éک…读و–¹و³•ï¼‰20120428.ppt
م€ٹè®،ç®—وœ؛程ه؛ڈ设è®،(Cè¯è¨€)م€‹ç¬¬7ç« -第2èٹ‚-ه‡½و•°çڑ„ه®ڑن¹‰.ppt
م€ٹ网络ه·¥ç¨‹è®¾è®،ن¸ژé،¹ç›®ه®è®م€‹02-ن؛¤وچ¢وœ؛هڈٹه…¶هں؛وœ¬é…چç½®.ppt
ه†…ه®¹و¦‚è¦پï¼ڑوœ¬و–‡و،£è¯¦ç»†ن»‹ç»چن؛†ه°†وœچهٹ،è؟پ移هˆ°Nacosو³¨ه†Œن¸ژé…چç½®ن¸ه؟ƒçڑ„ه…·ن½“و¥éھ¤ï¼ŒهŒ…و‹¬pomو–‡ن»¶ن¸ن¾èµ–هŒ…çڑ„و›´و–°م€پهگ¯هٹ¨ç±»و³¨è§£çڑ„و·»هٹ ن»¥هڈٹ详细çڑ„nacosه®¢وˆ·ç«¯ه’Œوœچهٹ،é…چç½®و–‡ن»¶è®¾ç½®م€‚هœ¨pomو–‡ن»¶ن¸ï¼Œéœ€è¦پ移除و—§çڑ„وœچهٹ،هڈ‘çژ°ه·¥ه…·ï¼ˆه¦‚Eureka)相ه…³ن¾èµ–ه¹¶ه¼•ه…¥ç‰¹ه®ڑ版وœ¬çڑ„nacos-clientهڈٹ相ه…³starter组ن»¶ï¼Œç،®ن؟springboot版وœ¬ن¸چن½ژن؛ژ2.2.3م€‚هگ¯هٹ¨ç±»éœ€و·»هٹ `@EnableDiscoveryClient`و³¨è§£ن»¥هگ¯ç”¨وœچهٹ،هڈ‘çژ°هٹں能م€‚é…چç½®و–‡ن»¶ن¸ï¼Œوکژç،®وŒ‡ه®ڑن؛†وœچهٹ،çڑ„هں؛وœ¬ن؟،وپ¯ï¼ˆه¦‚端هڈ£م€په؛”用هگچ称)م€پnacosوœچهٹ،ه™¨هœ°ه€م€په‘½هگچç©؛é—´م€پهˆ†ç»„ç‰ه…³é”®هڈ‚و•°ï¼Œه¹¶ه¼؛è°ƒن؛†é…چç½®و–‡ن»¶و ¼ه¼ڈن¸؛YAMLçڑ„é‡چè¦پو€§م€‚ه¯¹ن؛ژه·²هکهœ¨çڑ„وœچهٹ،,ن»…需ه®Œوˆگه‰چن¸‰ن¸ھو¥éھ¤ï¼Œè€Œه¯¹ن؛ژو–°çڑ„وœچهٹ،,هˆ™è؟ک需è؟›è،Œé…چç½®و–‡ن»¶çڑ„ه¯¼ه…¥ه·¥ن½œم€‚ 适هگˆن؛؛群ï¼ڑه¯¹ه¾®وœچهٹ،و¶و„وœ‰ن¸€ه®ڑن؛†è§£ï¼Œç‰¹هˆ«وک¯و£هœ¨è€ƒè™‘وˆ–ه·²ç»ڈه†³ه®ڑن»ژه…¶ن»–وœچهٹ،هڈ‘çژ°ه·¥ه…·è؟پ移至Nacosçڑ„ن¼پن¸ڑç؛§ه¼€هڈ‘者وˆ–è؟گç»´ن؛؛ه‘کم€‚ ن½؟用هœ؛و™¯هڈٹç›®و ‡ï¼ڑâ‘ ه¸®هٹ©ه›¢éکںه°†çژ°وœ‰هں؛ن؛ژه…¶ن»–وœچهٹ،هڈ‘çژ°وœ؛هˆ¶çڑ„ه؛”用程ه؛ڈه¹³و»‘è؟پ移هˆ°Nacosه¹³هڈ°ï¼›â‘،ç،®ن؟و–°ه¼€هڈ‘çڑ„وœچهٹ،能ه¤ںو£ç،®هœ°و³¨ه†Œهˆ°Nacosه¹¶ن½؟用ه…¶وڈگن¾›çڑ„é…چç½®ç®،çگ†هٹں能;③é€ڑè؟‡هگˆçگ†çڑ„é…چç½®ه‡ڈه°‘وœچهٹ،é—´çڑ„耦هگˆه؛¦ï¼Œوڈگé«کç³»ç»ںçڑ„هڈ¯ç»´وٹ¤و€§ه’Œو‰©ه±•و€§م€‚ éک…读ه»؛è®®ï¼ڑç”±ن؛ژو¶‰هڈٹهˆ°ه…·ن½“çڑ„版وœ¬هڈ·ه’Œé…چ置细èٹ‚,هœ¨ه®é™…و“چن½œè؟‡ç¨‹ن¸ه؛”ن¸¥و ¼وŒ‰ç…§و–‡و،£وŒ‡ه¯¼و‰§è،Œï¼ŒهگŒو—¶ه…³و³¨ه®کو–¹وœ€و–°هٹ¨و€پ,ç،®ن؟و‰€ن½؟用çڑ„版وœ¬وک¯وœ€ç¨³ه®ڑن¸”符هگˆé،¹ç›®éœ€و±‚çڑ„م€‚و¤ه¤–,ه»؛è®®هœ¨éç”ںن؛§çژ¯ه¢ƒن¸ه…ˆè،Œوµ‹è¯•ï¼ŒéھŒè¯پé…چç½®و— 误هگژه†چوژ¨ه¹؟هˆ°ç”ںن؛§çژ¯ه¢ƒم€‚
javaه¼€هڈ‘程ه؛ڈو±‡و€»-JavaEE-Buy