树形结构的数据在项目开发中比较常见,比如比较典型的是论坛主题留言。
每一个主题(节点)可以有n个留言(子节点)。这些留言又可以有自己的留言。因此这种结构就是一颗树。本文讨论的是数据库中如何存储这种树形结构。
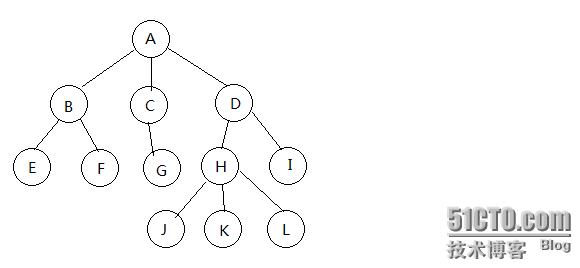
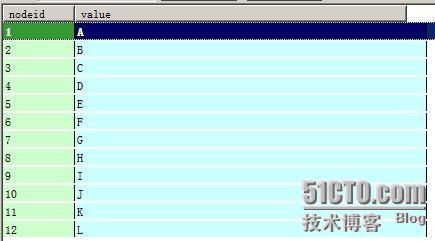
假设有如下一棵树:
方法一
注意:本例中的数据库是SQLite,因此SQL语句只对SQLite有效,其他数据库可以参考该写法。
要存储于数据库中,最简单直接的方法,就是存储每个元素的父节点ID。
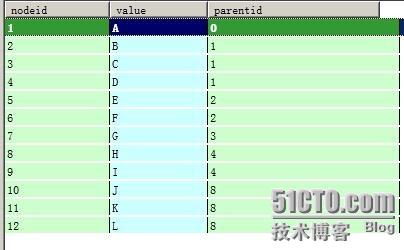
暂且把这种方法命名依赖父节点法,因此表结构设计如下:
存储的数据如下格式:
这种结构下,如果查询某一个节点的直接子节点,十分容易,比如要查询D节点的子节点。
|
1
|
select * from tree1 where parentid=4
|
如果要插入某个节点,比如在D节点下,再次插入一个M节点。
只需要如下SQL:
|
1
|
INSERT INTO tree1 (value,parentid) VALUES('M',4);
|
这种结构在查找某个节点的所有子节点,就稍显复杂,无论是SELECT还是DELETE都可能涉及到获取所有子节点的问题。比如要删除一个节点并且该节点的子节点也要全部删除,那么首先要获得所有子节点的ID,因为子节点并不只是直接子节点,还可能包含子节点的子节点。比如删除D节点及其子节点,必须先查出D节点下的所有子节点,然后再做删除,SQL如下:
|
1
2
3
4
|
select nodeid from tree1 where parentid=4 --返回8,9
select nodeid from tree1 where parentid in (8,9) --返回10,11,12
select nodeid from tree1 where parentid in (10,11,12) --返回空
delete from tree1 where nodeid in (4,8,9,10,11,12)
|
如果是只删除D节点,对于其它节点不做删除而是做提升,那么必须先修改子节点的parentid,然后才能删除D节点。
正如上面演示的,对于这种依赖父节点法,最大的缺点就是无法直接获得某个节点的所有子节点。因此如果要select所有的子节点,需要繁琐的步骤,这不利于做聚合操作。
对于某些数据库产品,支持递归查询语句的,比如微软的SQL Server,可以使用CTE技术实现递归查询。比如,要查询D节点的所有子节点。只需要如下语句:
|
1
2
3
4
5
6
|
WITH tmp AS(
SELECT * FROM Tree1 WHERE nodeid = 4
UNION ALL
SELECT a.* FROM Tree1 AS a,tmp AS b WHERE a.parentid = b. nodeid
)SELECT * FROM tmp
|
但是对于那些不支持递归查询的数据库来说,实现起来就比较复杂了。
方法二
还有一种比较土的方法,就是存储路径。暂且命名为路径枚举法。
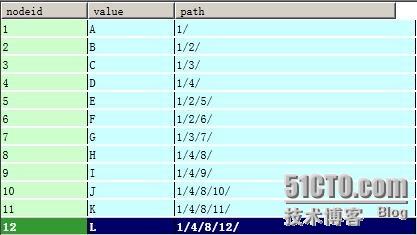
这种方法,将存储根结点到每个节点的路径。
这种数据结构,可以一眼就看出子节点的深度。
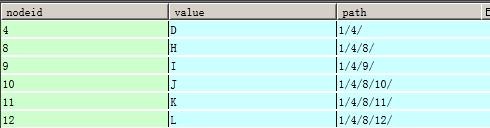
如果要查询某个节点下的子节点,只需要根据path的路径去匹配,比如要查询D节点下的所有子节点。
|
1
|
select * from tree2 where path like '%/4/%'
|
或者出于效率考虑,直接写成
|
1
|
select * from tree2 where path like '1/4/%'
|
如果要做聚合操作,也很容易,比如查询D节点下一共有多少个节点。
select count(*) from tree2 where path like '1/4/%';
要插入一个节点,则稍微麻烦点。要插入自己,然后查出父节点的Path,并且把自己生成的ID更新到path中去。比如,要在L节点后面插入M节点。
首先插入自己M,然后得到一个nodeid比如nodeid=13,然后M要插入到L后面,因此,查出L的path为1/4/8/12/,因此update M的path为1/4/8/12/13
|
1
2
3
4
5
|
update tree2 set
path=(select path from tree2 where nodeid=12) --此处开始拼接
||last_insert_rowid()||'/'
wherenodeid= last_insert_rowid(); |
这种方法有一个明显的缺点就是path字段的长度是有限的,这意味着,不能无限制的增加节点深度。因此这种方法适用于存储小型的树结构。
方法三
下面介绍一种方法,称之为闭包表。
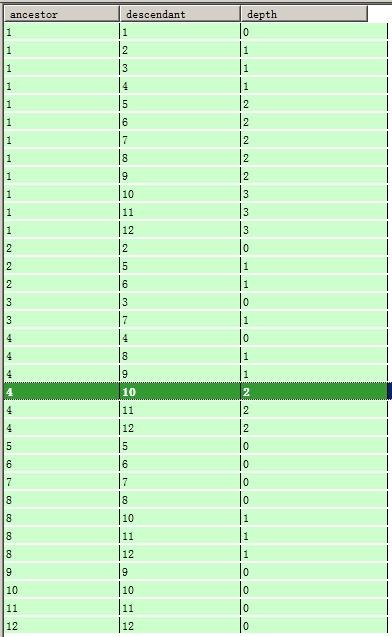
该方法记录了树中所有节点的关系,不仅仅只是直接父子关系,它需要使用2张表,除了节点表本身之外,还需要使用1张表来存储节祖先点和后代节点之间的关系(同时增加一行节点指向自身),并且根据需要,可以增加一个字段,表示深度。因此这种方法数据量很多。设计的表结构如下:
Tree3表:
NodeRelation表:
如例子中的树,插入的数据如下:
Tree3表的数据
NodeRelation表的数据
可以看到,NodeRelation表的数据量很多。但是查询非常方便。比如,要查询D节点的子元素
只需要
|
1
|
select * from NodeRelation where ancestor=4;
|
要查询节点D的直接子节点,则加上depth=1
|
1
|
select * from NodeRelation where ancestor=4 and depth=1;
|
要查询节点J的所有父节点,SQL:
|
1
|
select * from NodeRelation where descendant=10;
|
如果是插入一个新的节点,比如在L节点后添加子节点M,则插入的节点除了M自身外,还有对应的节点关系。即还有哪些节点和新插入的M节点有后代关系。这个其实很简单,只要和L节点有后代关系的,和M节点必定会有后代关系,并且和L节点深度为X的和M节点的深度必定为X+1。因此,在插入M节点后,找出L节点为后代的那些节点作为和M节点之间有后代关系,插入到数据表。
|
1
2
3
4
5
6
7
|
INSERT INTO tree3 (value) VALUES('M');--插入节点
INSERT INTO NodeRelation(ancestor,descendant,depth)
select n.ancestor,last_insert_rowid(),n.depth+1--此处深度+1作为和M节点的深度
from NodeRelation n
where n.descendant=12
Union ALL
select last_insert_rowid() ,last_insert_rowid(),0 --加上自身
|
在某些并不需要使用深度的情况下,甚至可以不需要depth字段。
如果要删除某个节点也很容易,比如,要删除节点D,这种情况下,除了删除tree3表中的D节点外,还需要删除NodeRelation表中的关系。
首先以D节点为后代的关系要删除,同时以D节点的后代为后代的这些关系也要删除:
|
1
2
|
delete from NodeRelation where descendant in
(select descendant from NodeRelation where ancestor=4 );--查询以D节点为祖先的那些节点,即D节点的后代。
|
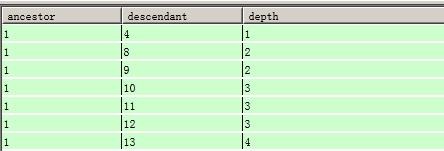
这种删除方法,虽然彻底,但是它也删除了D节点和它原本的子节点的关系。
如果只是想割裂D节点和A节点的关系,而对于它原有的子节点的关系予以保留,则需要加入限定条件。
限制要删除的关系的祖先不以D为祖先,即如果这个关系以D为祖先的,则不用删除。因此把上面的SQL加上条件。
|
1
2
3
|
delete from NodeRelation where descendant in
(select descendant from NodeRelation where ancestor=4 );--查询以D节点为祖先的那些节点,即D节点的后代。
and ancestor not in (select descendant from NodeRelation where ancestor =4 )
|
上面的SQL用文字描述就是,查询出D节点的后代,如果一个关系的祖先不属于D节点的后代,并且这个关系的后代属于D节点的后代,就删除它。
这样的删除,保留了D节点自身子节点的关系,如上面的例子,实际上删除的节点关系为:
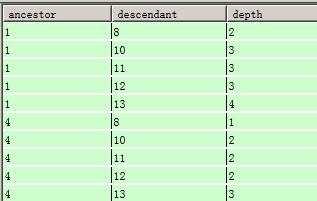
如果要删除节点H,则为
总结:
上面主要讲了3种方式,各有优点缺点。可以根据实际需要,选择合适的数据模型。











相关推荐
本篇文章将深入探讨树形控件的概念、功能以及如何在实际应用中使用它。 首先,理解树形控件的基本结构至关重要。它由根节点、子节点和叶节点组成,形成一个可扩展的树状结构。根节点是层次结构的起点,而子节点可以...
每棵树由若干节点构成,其中一个节点作为根节点,其它节点分成若干不相交的子树,每个子树又可以有若干子节点,如此递归下去。 在关系数据库中,存储树形结构数据有多种方式,其中主流的方法是使用邻接列表模型(The...
在数据库驱动的系统中,构建结构树是一种常见的需求,特别是在处理层次结构数据时,例如组织架构、文件目录或分类系统。本算法提供了一种高效的方法,能够根据数据库表中的记录自动生成结构树。 1. **数据库表结构...
总之,"d_tree一棵树结构"是用于权限管理的一种数据结构,通过遍历树节点来确定权限分配,而"node"文件很可能是存储这些树节点信息的载体。理解和掌握树的遍历、插入、删除等操作对于理解和实现这样的系统至关重要。
每个节点可以有子节点,形成一个父节点-子节点的关系,就像一棵倒置的树。在网页或应用程序中,这种菜单通常用于文件浏览器、网站导航或组织架构的展示。 动态获取树形菜单的核心在于将数据库中的数据转换成前端...
在Java编程中,生成一棵变更树涉及到数据结构和UI展示两个方面。变更树通常用于表示层级关系,例如文件系统、组织结构或者版本控制中的变更历史。在这个场景中,`BunshoCategoryFormatDto` 类定义了树节点的数据模型...
1. **层次数据库**:这是一种早期的数据库模型,数据结构像一棵树,每个节点只有一个父节点。 2. **网状数据库**:这是对层次数据库的一种改进,允许每个节点拥有多个父节点,形成网状结构。 3. **关系型数据库**:...
在Caché中,数据是以Global变量的形式存储的,它们以^符号开头,采用多维数组的形式,可以看作一棵树,每个节点都直接映射到磁盘和内存,从而实现快速访问。例如,^AirPlane("Manufacturer","Address","Country")=...
每个PDBR是一个片段型的集合,形成一棵层次树结构,其中的根片段值和其后代片段值共同构成数据库记录或实例。 数据库模式定义是IMS数据模型的基础,它是一组PDBR型的集合,每个PDBR型由DBD语句群定义,描述了数据的...
总之,“数据库-表-树节点读取”这一主题涵盖了许多数据库设计和查询技术,涉及到如何在数据库中有效地表示、存储和检索树形结构的数据。通过理解并熟练运用上述方法,开发人员可以构建出更高效、更易于维护的数据库...
本题目的目标是读取名为"dir.txt"的文本文件,并将其内容转换为一棵树。这个任务涉及到文本解析、数据结构的理解以及编程技巧。下面我们将详细探讨如何实现这一过程。 首先,我们需要理解"dir.txt"文件的内容。通常...
- **创建**:构建一棵树通常始于一个根节点,然后根据需求添加子节点。可以使用链表或数组实现。 - **遍历**:包括前序遍历(根-左-右)、中序遍历(左-根-右)和后序遍历(左-右-根)。这些遍历方法对于查找、...
根节点可能是一棵B+树的唯一节点,也可能有多个子节点。叶子节点之间通过指针链接,形成一条连续的链表,便于区间查询。 **B+树的操作** 1. **插入操作**:当插入新的元素时,B+树会首先找到对应的叶子节点。如果该...
分类数据结构本质上就是一棵树,每个节点代表一个分类,节点之间的关系则反映了分类的上下级关系。 首先,我们需要理解如何在数据库中存储树形结构。一个基本的方案是创建一个表,例如`Catalog`,包含以下字段: 1....
在数据库设计中,树形结构是一种常见的数据组织方式,尤其在表示层次关系时非常有用,如文件系统、组织架构或评论回复等。本篇主要讨论的是在SQL数据库中如何使用邻接列表(Adjacency List)模型来实现树形结构,并...
二叉树是一种常见的数据结构,在计算机科学中有广泛的应用。一个二叉树由节点组成,每个节点最多有两个子节点,分别称为左子节点和右子节点。二叉树可以是空树,也可以包含一个或多个节点。 #### 完全二叉树定义: ...
- **层次型数据库**将数据组织成一棵树形结构,其中每一个节点都有一个父节点(除了根节点外),这种模型在处理特定类型的数据关系时非常有效。 - **网络型数据库**与层次型类似,但允许一个节点有多个父节点,能够...
- **多棵树**:系统可能需要管理多棵独立的树,如部门结构、分类结构等,此时需要设计一个支持多树的系统。 - **动态增删改**:菜单结构可能需要动态调整,数据库设计应能方便地支持插入、删除和更新操作。 总之...
知识点3:在一棵二叉树上第 5 层的结点数最多是 2 的(5-1)次方。 知识点4:结构化程序设计风格应该使用顺序、选择和重复(循环)三种基本控制结构表示程序的控制逻辑,不使用 goto 语句。 知识点5:面向对象方法...