阿达马变换的简单介绍

jubincn

浏览: 242520 次
性别:
来自: 宁波

最近访客更多访客>>

yych007

bardo

stephenworld

裴喜龙

博主相关

博客

微博

相册

留言

关于我

文章分类

全部博客 (297)

社区版块

存档分类

注：内容基本上摘抄自wikipedia，链接：http://zh.wikipedia.org/wiki/%E9%98%BF%E8%BE%BE%E9%A9%AC%E5%8F%98%E6%8D%A2

阿达马变换（Hadamard transform），或称沃尔什-阿达玛转换，是一种广义傅立叶变换（Fourier transforms），作为变换编码的一种在视频编码当中使用有很久的历史。在近来的视频编码标准中，阿达马变换多被用来计算SATD(一种视频残差信号大小的衡量)。

变换矩阵

在H.264中使用了4阶和8阶的阿达马变换来计算SATD，其变换矩阵为：

$H_4 = \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \end{bmatrix}$

$H_8 = \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 & 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 & 1 & -1 & -1 & 1 \\ 1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 \\ 1 & -1 & 1 & -1 & -1 & 1 & -1 & 1 \\ 1 & 1 & -1 & -1 & -1 & -1 & 1 & 1 \\ 1 & -1 & -1 & 1 & -1 & 1 & 1 & -1 \end{bmatrix}$

SATD计算方法

当计算4x4块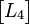 $\begin{bmatrix}L_4\end{bmatrix}$ 的SATD时，先使用下面的方法进行二维的阿达马变换：

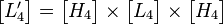
$\begin{bmatrix} L_4' \end{bmatrix}= \begin{bmatrix} H_4 \end{bmatrix}\times \begin{bmatrix} L_4 \end{bmatrix}\times \begin{bmatrix} H_4 \end{bmatrix}$

然后计算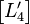 $\begin{bmatrix}L_4'\end{bmatrix}$ 所有系数绝对值之和并归一化。

类似的，当计算8x8块 $\begin{bmatrix}L_8\end{bmatrix}$ 的SATD时，先使用下面的方法进行二维的Hadamard变换：

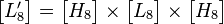
$\begin{bmatrix} L_8' \end{bmatrix}= \begin{bmatrix} H_8 \end{bmatrix}\times \begin{bmatrix} L_8 \end{bmatrix}\times \begin{bmatrix} H_8 \end{bmatrix}$

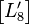然后计算 $\begin{bmatrix}L_8'\end{bmatrix}$ 所有系数绝对值之和并归一化。

建构阿达马变换

阿达马变换转换主要型式为 $\boldsymbol{2^k}$ 点的转换矩阵，其最小单位矩阵为 2x2 的阿达马变换矩阵，以下分别为二点、四点与如何产生 $\boldsymbol{2^k}$ 点的阿达马变换转换步骤。

二点阿达马变换转换：

$\boldsymbol{W_2} = \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}$

四点阿达马变换转换：

$\boldsymbol{W_4} = \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \\ 1 & -1 & 1 & -1 \end{bmatrix}$

产生 $\boldsymbol{2^k}$ 点阿达马变换的步骤：

步骤一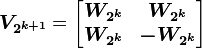： $\boldsymbol{V_{2^{k+1}}} = \begin{bmatrix} \boldsymbol{W_{2^k}} & \boldsymbol{W_{2^k}} \\ \boldsymbol{W_{2^k}} & \boldsymbol{-W_{2^k}} \end{bmatrix}$

步骤二：根据正负号次序 (Sign change,正负号改变次数) 将矩阵(Matrix) 内的列向量座顺序上的重新排列。

$\boldsymbol{V_{2^{k+1}}} \longrightarrow \boldsymbol{W_{2^{k+1}}}$

范例

$\boldsymbol{V_4} = \begin{bmatrix} \boldsymbol{W_2} & \boldsymbol{W_2} \\ \boldsymbol{W_2} & \boldsymbol{-W_2} \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \end{bmatrix} ,\quad \boldsymbol{W_4} = \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \\ 1 & -1 & 1 & -1 \end{bmatrix}.$

$\boldsymbol{V_8} = \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & -1 & -1 & 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 & 1 & -1 & -1 & 1 \\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\ 1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 \\ 1 & 1 & -1 & -1 & -1 & -1 & 1 & 1 \\ 1 & -1 & -1 & 1 & -1 & 1 & 1 & -1 \\ 1 & -1 & 1 & -1 & -1 & 1 & -1 & 1 \end{bmatrix}, \quad \boldsymbol{W_8} = \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 \\ 1 & 1 & -1 & -1 & -1 & -1 & 1 & 1 \\ 1 & 1 & -1 & -1 & 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 & 1 & -1 & -1 & 1 \\ 1 & -1 & -1 & 1 & -1 & 1 & 1 & -1 \\ 1 & -1 & 1 & -1 & -1 & 1 & -1 & 1 \\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \end{bmatrix}.$

优缺点比较

优点

仅需实数运算 (Real operation) 。
不需乘法运算 (No multiplication) ，仅有加减法运算。
有部分性质类似于离散傅立叶变换(Discrete fourier transform) 。
顺向转换 (Forward transform) 与反向转换 (Inverse transform ) 型式为相似式。

$\begin{cases} \begin{matrix} F\left[ m \right] &=& \sum_{n=0}^{N-1} W\left[ {m, n} \right] f\left[ n \right] & & (\mbox{Forward Type}) \\ f\left[ n \right] &=& \left( \frac{1}{N} \right) \sum_{n=0}^{N-1} W\left[ {m, n} \right]F\left[ m \right] & &(\mbox{Inverse Type}) \end{matrix} \end{cases},$

其中 $F\left[ n \right]$ 与 $f\left[ n \right]$ 分别都为行向量(Column vector) 。

缺点

其收敛速度较离散余弦变换慢，因此对于频谱分析的效果较差。
其加减法量较离散傅立叶变换、离散余弦变换多。

应用范围

阿达马变换转换主要为一种非常适合应用于频域分析 (Spectrum analysis) ，去执行快速之分析。可惜的是对于折积性质是一种逻辑折积，与离散傅立叶变换上之折积性质截然不同。因此，较折积上无法取代离散傅立叶变换。

分享到：

视频编码中的PAFF和MBAFF的区别转自：ht ... | H264 编解码框架简介转自：http://blog. ...

2011-11-01 15:55
浏览 2816
评论(0)
查看更多

发表评论

您还没有登录,请您登录后再发表评论

最近访客更多访客>>

博主相关

文章分类

社区版块

存档分类

最新评论