快速傅立叶变换（Fast Fourier Transform）

FFT算法是由J.W. Cooley和J. W. Tukey在论文”Analgorithm for the machine calculation of complex Fourier Series”中提出的。FFT是基于ComplexDFT来实现的。

通过ComplexDFT来计算Real DFT

尽管FFT算法是基于ComplexDFT实现的，但我们仍可以用其来计算RealDFT，因为RealDFT可以方便地转换为ComplexDFT。从图2-1中可以看出RealDFT和Complex DFT的区别。在RealDFT中，时间域是一个包含N个点的信号，频率域则包括实数部分和虚数部分两个长度为N/2+1的信号；在ComplexDFT中，时间域也有两个部分，分别是实数部分和虚数部分，长度为N。频率域的实数部分和虚数部分则长度增至N。

如图2-1所示，RealDFT和ComplexDFT的区别仅在于后者在时间域增加了一个虚数部分，频率域长度的变化正是由这个虚数部分引起的。

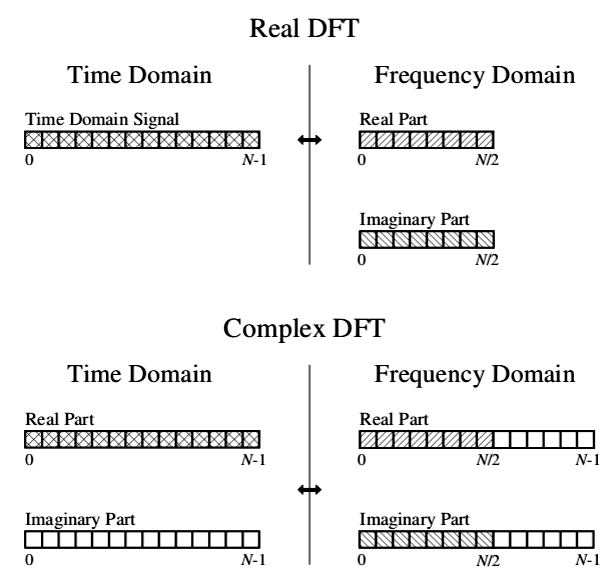
图2-1 Real DFT和ComplexDFT的区别

产生这个区别的原因是实数的虚数部分为0，因此将实数表达为虚数很简单，加上一个系数为0的虚数部分即可。例如在图2-1中的ComplexDFT，若将时间域的虚数部分设为0，频率域中多出的部分也置为0，那么图2-1中的RealDFT和ComplexDFT就相等了。当包含负频率时，DFT的频率域会具有周期性。在ComplexDFT中，频率域中0到N/2为正频率，N/2+1到N-1为负频率。

与使用ComplexDFT计算Real DFT相比，使用ComplexInverse DFT计算Real InverseDFT更为困难。这是因为频率域中N/2+1到N-1部分的系数需要计算。其计算过程也不复杂，系数N/2+1对应系数N/2-1的相反数，N/2+2对应N/2-2的相反数，即：

系数（N/2+1）=—系数（N/2-1）

系数（N/2+2）=—系数（N/2-2）

注意，0与N/2没有相应的点与之对应。进行RealInverse DFT计算时，首先将0到N/2复制到complexDFT的系数0到N/2，然后使用一个子过程来计算系数N/2+1到N-1。这个子过程的伪代码实现如下：

6000'NEGATIVE FREQUENCY GENERATION

6010'This subroutine creates the complex frequency domain from therealfrequency domain.

6020'Upon entry to this subroutine, N% contains the number of points inthesignals, and

6030'REX[ ] and IMX[ ] contain the real frequency domain in samples 0toN/2.

6040'On return, REX[ ] and IMX[ ] contain the complex frequencydomainin samples 0 to N-1.

6050 '

6060FOR K% = (N%/2+1) TO (N%-1)

6070REX[K%] = REX[N%-K%]

6080IMX[K%] = -IMX[N%-K%]

6090NEXT K%

6100 '

6110RETURN

FFT的实现原理

FFT算法很复杂，本文不讨论细节，只描述其实现原理。在虚数域中，时间域和频率域表达的都是由N个虚数点组成的信号，每个虚数点都由实数部分和虚数部分的两个数字来表达。例如虚数点X[6]，就是由实数部分ReX[6]和虚数部分Im X[6]组成。

FFT算法的核心思想是将时间域中一个包含N个点的信号分解为N个包含一个点的信号。然后分别计算这N个信号的频率域对应值，最后将这N个频率域的信号综合为频率域中的一个信号。

图2-2描述了一个包含12个点的示例信号在FFT中的分解过程。

图2-2 FFT中的分解(decompose)过程

图2-2中的过程看似复杂，实际上可以通过如图2-3所示的位反转算法(bitreversal sorting)来实现。算法将各点的二进制位反转为对称的形式，即可完成N个点的信号到N个单点信号的分解过程。

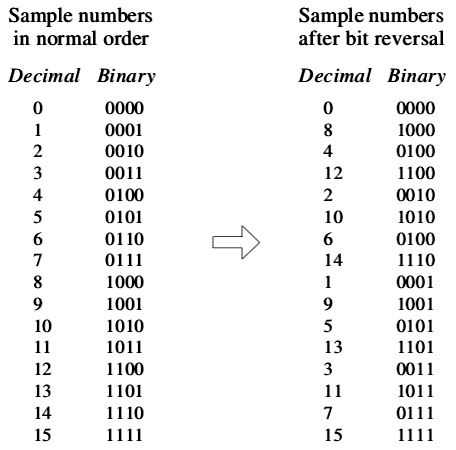
图2-3位反转排序

FFT算法的下一步是分别求出这N个单点信号在频率域的振幅。这是算法中最容易的一步，单点的振幅等于它自己本身的值，这意味着在这一步什么也不必做。

算法的最后一步是将这N个频率域的点按在时间域分解时的反序结合(combine)起来，这里不能使用位反转算法，这一步是算法中最复杂的部分。

图2-4展现了两个长度为4的频率域信号组合为一个长度为8的频率域信号的过程。组合(synthesis)的顺序必须与在时间域中分解(decompose)的过程完全相逆。以时间域的信号abcd和信号efgh为例，要将其整合为一个包含8个点的信号需要经过这两步：首先将这两个信号进行稀释（dilute），即用0填充为长度为8的信号，然后两者相加即可得到新的信号。如abcd稀释后得到a0b0c0d0，efgh稀释后得到0e0f0g0h，两者相加可得abcdefgh。

图2-4FFT组合（synthesis）

当时间域用0稀释时，对应的频率域会复制自己。

当时间域先移位再用0填充时，对应的频率域会乘以一个三角函数，然后再复制自己。

abcd与efgh的稀释方法并不相同，abcd稀释为a0b0c0d0，其偶数位为0；efgh稀释为0e0f0g0h，其奇数位为0。也就是说efgh向右移动了一位，这个在时间域的移位对应于频率域乘以一个三角函数。

图2-5展示了在两个频率域中长度为4的信号组合的过程。左侧的Odd-Four Point Frequency Spectrum指的是对应奇数位为0的时间域信号的频率域信号，如EFGH；右侧的Even-Four Point Frequency Spectrum指的是对应偶数位为0的时间域信号的频率域信号，如ABCD。

为了更清楚地表达这个过程，图2-6将其中的两个点拿出来，因为这个图形很想一只张开翅膀的蝴蝶，因此人们也将这个图所代表的过程称之为butterfly。

图2-5 FFT组合过程

图2-6 Butterfly

图2-7显示了FFT变换的流程图，包含了FFT变换的三个部分。1.时间域的分解过程可以通过位变换算法来实现。2.将时间域分解后得到的N个单点转换为频率域并不需要任何计算，因为对于单点而言，在频率域的振幅等于时间域的振幅。3.第三部分是整个算法的核心，是图中重点要表达的部分。

图2-7FFT流程图

在图2-7中，最外面的循环表示要在lgN个层次上进行组合（synthesis），中间那层循环指在每一层上的组合过程，最内部的循环表示butterfly过程。

下面是FFT算法的一段Basic代码：

1000'THE FAST FOURIER TRANSFORM

1010'Upon entry, N% contains the number of points in the DFT, REX[ ] and

1020'IMX[ ] contain the real and imaginary parts of the input. Uponreturn,

1030'REX[ ] and IMX[ ] contain the DFT output. All signals run from 0 toN%-1.

1040'

1050PI = 3.14159265 'Set constants

1060NM1% = N%-1

1070ND2% = N%/2

1080M% = CINT(LOG(N%)/LOG(2))

1090J% = ND2%

1100'

1110FOR I% = 1 TO N%-2 'Bit reversal sorting

1120IF I% >= J% THEN GOTO 1190

1130TR = REX[J%]

1140TI = IMX[J%]

1150REX[J%] = REX[I%]

1160IMX[J%] = IMX[I%]

1170REX[I%] = TR

1180IMX[I%] = TI

1190K% = ND2%

1200IF K% > J% THEN GOTO 1240

1210J% = J%-K%

1220K% = K%/2

1230GOTO 1200

1240J% = J%+K%

1250NEXT I%

1260'

1270FOR L% = 1 TO M% 'Loop for each stage

1280LE% = CINT(2^L%)

1290LE2% = LE%/2

1300UR = 1

1310UI = 0

1320SR = COS(PI/LE2%) 'Calculate sine & cosine values

1330SI = -SIN(PI/LE2%)

1340FOR J% = 1 TO LE2% 'Loop for each sub DFT

1350JM1% = J%-1

1360FOR I% = JM1% TO NM1% STEP LE% 'Loop for each butterfly

1370IP% = I%+LE2%

1380TR = REX[IP%]*UR – IMX[IP%]*UI 'Butterfly calculation

1390TI = REX[IP%]*UI + IMX[IP%]*UR

1400REX[IP%] = REX[I%]-TR

1410IMX[IP%] = IMX[I%]-TI

1420REX[I%] = REX[I%]+TR

1430IMX[I%] = IMX[I%]+TI

1440NEXT I%

1450TR = UR

1460UR = TR*SR - UI*SI

1470UI = TR*SI + UI*SR

1480NEXT J%

1490NEXT L%

1500'

1510RETURN

更快的FFT算法

有多种方法可以加速FFT算法，但也只能达到20%– 40%的加速比。例如在时间域分解时，提前两步、在每个信号包含四个点时结束分解。另一种方法是将时间域的虚数部分设为0，从而使得频率域的振幅具有对称的性质，即将复数FFT算法转换为实数FFT算法。下面是实数InverseFFT算法的伪代码：

4000'INVERSE FFT FOR REAL SIGNALS

4010'Upon entry, N% contains the number of points in the IDFT, REX[ ]and

4020'IMX[ ] contain the real and imaginary parts of the frequency domainrunning from

4030'index 0 to N%/2. The remaining samples in REX[ ] and IMX[ ] areignored.

4040'Upon return, REX[ ] contains the real time domain, IMX[ ] containszeros.

4050'

4060'

4070FOR K% = (N%/2+1) TO (N%-1)'Make frequency domain symmetrical

4080REX[K%] = REX[N%-K%]'(as in Table 12-1)

4090IMX[K%] = -IMX[N%-K%]

4100NEXT K%

4110'

4120FOR K% = 0 TO N%-1'Add real and imaginary parts together

4130REX[K%] = REX[K%]+IMX[K%]

4140NEXT K%

4150'

4160GOSUB 3000‘Calculateforward real DFT (TABLE 12-6)

4170'

4180FOR I% = 0 TO N%-1'Add real and imaginary parts together

4190REX[I%] = (REX[I%]+IMX[I%])/N%'and divide the time domain by N%

4200IMX[I%] = 0

4210NEXT I%

4220'

4230RETURN

图2-8展示了FFT中使用的对称性原理。a和b分别表示同一个时间域信号，虚数部分全部为0，c和d分别是对应在频率域实数部分和虚数部分。c具有偶对称的性质，d具有奇对称的性质。

图2-8DFT中实数部分的对称

图2-9DFT中虚数部分的对称

图2-9与图2-8类似，其时间域实数部分a为0，虚数部分b非0，对应的频率域曲线c和d分别具有奇对称和偶对称的性质。

上面介绍了时间域的某个部分为0的情况，如果时间域的实数部分和虚数部分都不为0情况会怎样？频率域可以通过两个或多个频谱的相加获得。关键点在于：频率域具有这两种对称性质（奇对称和偶对称）的波谱可以完美地分为两个分量。输入信号被分为来两个部分，N/2个奇数位信号被放置在时间域信号的实数部分，N/2个偶数位信号被放置在时间域信号的虚数部分，从而使得长度为N的FFT变换转化为长度为N/2的FFT变换。频率域此时有两个长度为N/2的信号，将其组合起来（使用FFT中的方法）即可得到RealFFT变换的结果。下面是这种算法的伪代码实现：

3000'FFT FOR REAL SIGNALS

3010'Upon entry, N% contains the number of points in the DFT, REX[ ]contains

3020'the real input signal, while values in IMX[ ] are ignored. Uponreturn,

3030'REX[ ] and IMX[ ] contain the DFT output. All signals run from 0 toN%-1.

3040'

3050NH% = N%/2-1'Separate even and odd points

3060FOR I% = 0 TO NH%

3070REX(I%) = REX(2*I%)

3080IMX(I%) = REX(2*I%+1)

3090NEXT I%

3100'

3110N% = N%/2'Calculate N%/2 point FFT

3120GOSUB 1000

3130N% = N%*2

3140'

3150NM1% = N%-1'Even/odd frequency domain decomposition

3160ND2% = N%/2

3170N4% = N%/4-1

3180FOR I% = 1 TO N4%

3190IM% = ND2%-I%

3200IP2% = I%+ND2%

3210IPM% = IM%+ND2%

3220REX(IP2%) = (IMX(I%) + IMX(IM%))/2

3230REX(IPM%) = REX(IP2%)

3240IMX(IP2%) = -(REX(I%) - REX(IM%))/2

3250IMX(IPM%) = -IMX(IP2%)

3260REX(I%) = (REX(I%) + REX(IM%))/2

3270REX(IM%) = REX(I%)

3280IMX(I%) = (IMX(I%) - IMX(IM%))/2

3290IMX(IM%) = -IMX(I%)

3300NEXT I%

3310REX(N%*3/4) = IMX(N%/4)

3320REX(ND2%) = IMX(0)

3330IMX(N%*3/4) = 0

3340IMX(ND2%) = 0

3350IMX(N%/4) = 0

3360IMX(0) = 0

3370'

3380PI = 3.14159265'Complete the last FFT stage

3390L% = CINT(LOG(N%)/LOG(2))

3400LE% = CINT(2^L%)

3410LE2% = LE%/2

3420UR = 1

3430UI = 0

3440SR = COS(PI/LE2%)

3450SI = -SIN(PI/LE2%)

3460FOR J% = 1 TO LE2%

3470JM1% = J%-1

3480FOR I% = JM1% TO NM1% STEP LE%

3490IP% = I%+LE2%

3500TR = REX[IP%]*UR - IMX[IP%]*UI

3510TI = REX[IP%]*UI + IMX[IP%]*UR

3520REX[IP%] = REX[I%]-TR

3530IMX[IP%] = IMX[I%]-TI

3540REX[I%] = REX[I%]+TR

3550IMX[I%] = IMX[I%]+TI

3560NEXT I%

3570TR = UR

3580UR = TR*SR - UI*SI

3590UI = TR*SI + UI*SR

3600NEXT J%

3610RETURN