离散余弦变换（Discrete Cosine Transform）

DCT变换和FFT变换都属于变换压缩方法(TransformCompression)，变换压缩的一个特点是将从前密度均匀的信息分布变换为密度不同的信息分布。在图像中，低频部分的信息量要大于高频部分的信息量，尽管低频部分的数据量比高频部分的数据量要小的多。例如删除掉占50%存储空间的高频部分，信息量的损失可能还不到5%。

变换编码有很多种。K–L变换的压缩效率很高，但算法实现困难；FFT变换算法实现简单，但压缩效率不是很理想。经过多方面的比较，最终胜出的算法是DCT，一种源自FFT的变换编码。

与FFT变换同时使用正弦和余弦函数来表达信号不同，DCT只使用余弦函数来表达信号。DCT变换有多个版本，有一种常用的DCT实现过程是这样的：对一个长度为129（0到128）的信号进行DCT变换。首先，复制点127到点1，使整个信号变为：

0, 1, 2, .., 127, 128, 127, …, 2, 1

     这串长度为256的时间域信号经过FFT变换后会生成一个长度为129的信号。因为时间域的信号对称，根据二元性（duality），对应的频率域信号的虚数部分全部为0。也就是说，我们输入的长度为129的时间域信号经过DCT变换后，产生一个长度为129的频率域信号，并且频率域完全由余弦函数组成。

     在图像处理中，每副图像都会被切成8×8的小块，块的大小可以是任意，只是因为历史原因人们习惯于切为8×8的块。二维的图像处理与一维的信号处理原理是一致的，只是一些计算公式不一样，在二维图像中，基函数的公式如下：

     公式中x和y指像素在空间域（对应一维的时间域）的坐标，u和v指基函数频率域中的坐标。这个基函数公式基于8×8的块，x,y, u, v的取值范围都是0–7。
图像经DCT变换后，低频信息集中在矩阵的左上角，高频信息则向右下角集中。直流分量在[0,0]处，[0,1]处的基函数在一个方向上是一个半周期的余弦函数，在另一个方向上是一个常数。[1,0]处的基函数与[0,1]类似，只不过方向旋转了90度。

图3-1 DCT变换中使用的基函数

图3-1是一个8×8的基函数示意图，从中拿出了6个基函数并做出其在二维平面上的示意图。这些基函数是不变的，在DCT变换中，这些基函数将与空间域中的每一个元素进行分别相乘，并将结果累加起来，就完成了空间域到频率域的初步变换。此时还需要两步就可以完成DCT变换：1.将第0行和第0列的值除以2（也就是说，[0,0]要除以4）。2.所有64个元素都除以16。

DCT反变换(InverseDCT)更为容易，将频率域中的基函数分别与对应的振幅(spectrum)相乘并累加，即可得到相应的空间域元素的值。

图3-2 JPEG中DCT转换示例

在图3-2中，最右侧的那一栏表示使用不同比特数来表达频率域的效果。原始频率域需要64个bit来存储，而g对应的频率域使用10个bit来存储频率域中的单个元素，h和i对应的频率域分别使用8个bit和5个bit。然后对d,e和f分别进行InverseDCT变换，g,h和i分别是使用原始空间域的值来减掉反变换(IDCT)后得到的残差。从图g可以看出，使用DCT压缩将一个32bit的块压缩为10bit，但信息损失很小，几乎可以忽略。从图h和i可以看出，随压缩率的增大，信息损失也逐渐变大。

经过DCT变换，压缩还可以通过丢弃64个振幅（Spectrum）中的一些信息量较小的元素来实现，这样即可以实现压缩，还可以尽可能最大地保持信息。

图3-3显示了使用不同数量的频率域振幅(Spectrum)所得的重建图像（a,b和c）与原始图像d的对比效果。从图c可以看出，即使弃掉占总数3/4的高频振幅（Spectrum），使用占总数1/4的低频振幅(Spectrum)也可以得到与原始图像很接近的结果。而且误差看起来是随机分布的，可以看作是随机噪声。

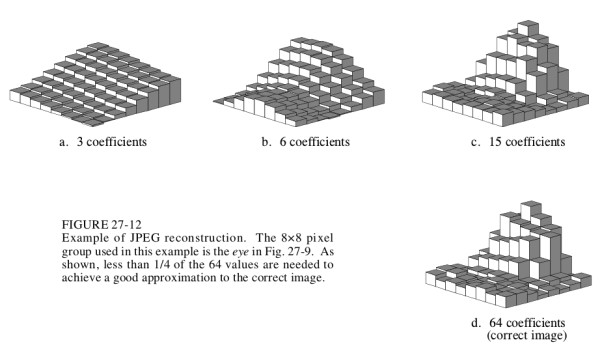
图3-3使用不同数量的Spectrum重建JPEG的效果

下面使用JPEG的压缩过程来介绍DCT变换在图像处理中的应用。JPEG的压缩过程可以分为以下几步：1.将整副图像分解为8×8的小块。2.对每个小块做DCT变换。3.对变换后得到的频率域使用前面所介绍的方法进行压缩：减少每个元素的bit值以及丢弃一些元素。通过量化表（QuantizationTable），这两个压缩操作可以一步实现。

图3-4是两个JPEG量化表的示例，频率域中的每个振幅（Spectrum）与量化表中对应的元素想除，即可得到压缩后的频率域。量化表a的压缩率较低，表b的压缩率比较高。例如a中最右下角的值为16，将对应振幅（Spectrum）的取值范围由-127– 127缩小为-7– 7。而在图b中右下角的值为256，将其清零，相当于将对应的高频信息删除。

图3-4 JPEG量化表

JPEG压缩的第四步，8×8的块被扫描为线性序列，扫描顺序如图3-5所示。对块进行量化处理后，再进行游程编码，那些振幅（Spectrum）为0的元素就被删除掉了。

图3-5线性扫描顺序

JPEG压缩第五步是对线性序列进行游程编码，第六步是对游程编码后的序列进行Huffman编码。

JPEG的压缩率可以设定，图3-6显示不同压缩率的图像与原始图像的对比。

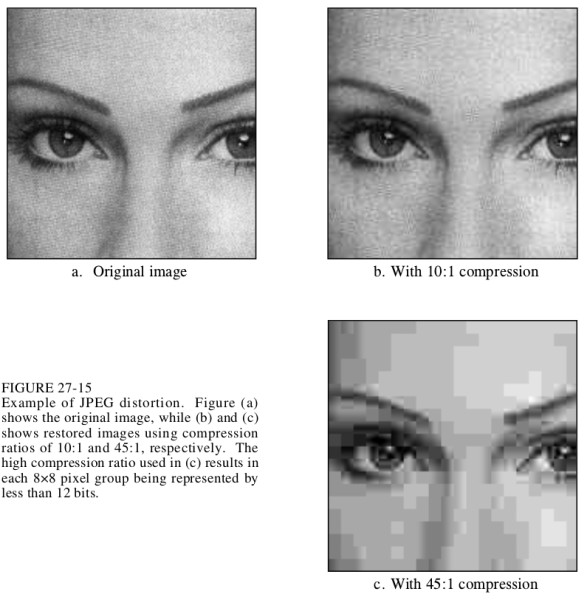
图3-6不同压缩率的JPEG对比

为什么DCT变换对图像的压缩效果要比DFT好？主要原因是DCT中使用了半周期的基函数，而DFT使用的是整周期基函数。图像中大部分像素的变化都是渐变的，因此DCT可以更好地表达图像，从而获得更高的压缩效率。