Calculate distance, bearing and more between

This page presents a variety of calculations for lati­tude/longi­tude points, with the formulæ and code fragments for implementing them.

All these formulæ are for calculations on the basis of a spherical earth (ignoring ellipsoidal effects) – which is accurate enough* for most purposes… [In fact, the earth is very slightly ellipsoidal; using a spherical model gives errors typically up to 0.3%1 – see notes for further details].

Great-circle distance between two points

Enter the co-ordinates into the text boxes to try out the calculations. A variety of formats are accepted, principally:

• deg-min-sec suffixed with N/S/E/W (e.g. 40°44′55″N, 73 59 11W), or
• signed decimal degrees without compass direction, where negative indicates west/south (e.g. 40.7486, -73.9864):

Point 1:	,
Point 2:	,

Distance:	km (to 4 SF*)
Initial bearing:
Final bearing:
Midpoint:

And you can see it on a map (aren’t those Google guys wonderful!)

Distance

This uses the ‘haversine’ formula to calculate the great-circle distance between two points – that is, the shortest distance over the earth’s surface – giving an ‘as-the-crow-flies’ distance between the points (ignoring any hills they fly over, of course!).

Haversine formula:	a = sin²(Δφ/2) + cos φ1 ⋅ cos φ2 ⋅ sin²(Δλ/2)
c = 2 ⋅ atan2( √a, √(1−a) )
d = R ⋅ c
where	φ is latitude, λ is longitude, R is earth’s radius (mean radius = 6,371km); note that angles need to be in radians to pass to trig functions!
JavaScript:	var R = 6371e3; // metres var φ1 = lat1.toRadians(); var φ2 = lat2.toRadians(); var Δφ = (lat2-lat1).toRadians(); var Δλ = (lon2-lon1).toRadians(); var a = Math.sin(Δφ/2) * Math.sin(Δφ/2) + Math.cos(φ1) * Math.cos(φ2) * Math.sin(Δλ/2) * Math.sin(Δλ/2); var c = 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1-a)); var d = R * c;

Note in these scripts, I generally use lat/lon for lati­tude/longi­tude in degrees, and φ/λ for lati­tude/longi­tude in radians – having found that mixing degrees & radians is often the easiest route to head-scratching bugs...

Historical aside: The height of tech­nology for navigator’s calculations used to be log tables. As there is no (real) log of a negative number, the ‘versine’ enabled them to keep trig func­tions in positive numbers. Also, the sin²(θ/2) form of the haversine avoided addition (which en­tailed an anti-log lookup, the addi­tion, and a log lookup). Printedtables for the haver­sine/in­verse-haver­sine (and its log­arithm, to aid multip­lica­tions) saved navi­gators from squaring sines, com­puting square roots, etc – arduous and error-prone activ­ities.

The haversine formula1 ‘remains particularly well-conditioned for numerical computa­tion even at small distances’ – unlike calcula­tions based on thespherical law of cosines. The ‘(re)versed sine’ is 1−cosθ, and the ‘half-versed-sine’ is (1−cosθ)/2 or sin²(θ/2) as used above. Once widely used by navigators, it was described by Roger Sinnott in Sky & Telescope magazine in 1984 (“Virtues of the Haversine”): Sinnott explained that the angular separa­tion between Mizar and Alcor in Ursa Major – 0°11′49.69″ – could be accurately calculated on a TRS-80 using the haversine.

For the curious, c is the angular distance in radians, and a is the square of half the chord length between the points.

If atan2 is not available, c could be calculated from 2 ⋅ asin( min(1, √a) )(including protec­tion against rounding errors).

Using Chrome on a middling Core i5 PC, a distance calcula­tion takes around 2 – 5 micro­seconds (hence around 200,000 – 500,000 per second). Little to no benefit is obtained by factoring out common terms; probably the JIT compiler optimises them out.

Spherical Law of Cosines

In fact, JavaScript (and most modern computers & languages) use ‘IEEE 754’ 64-bit floating-point numbers, which provide 15 significant figures of precision. By my estimate, with this precision, the simple spherical law of cosines formula (cos c = cos a cos b + sin a sin b cos C) gives well-condi­tioned results down to distances as small as a few metres on the earth’s surface. (Note that the geodetic form of the law of cosines is rearranged from the canonical one so that the latitude can be used directly, rather than the colatitude).

This makes the simpler law of cosines a reasonable 1-line alternative to the haversine formula for many geodesy purposes (if not for astronomy). The choice may be driven by programming language, processor, coding context, available trig func­tions (in different languages), etc – and, for very small distances an equirectangular approxima­tion may be more suitable.

Law of cosines:	d = acos( sin φ1 ⋅ sin φ2 + cos φ1 ⋅ cos φ2 ⋅ cos Δλ ) ⋅ R
JavaScript:	var φ1 = lat1.toRadians(), φ2 = lat2.toRadians(), Δλ = (lon2-lon1).toRadians(), R = 6371e3; // gives d in metres var d = Math.acos( Math.sin(φ1)*Math.sin(φ2) + Math.cos(φ1)*Math.cos(φ2) * Math.cos(Δλ) ) * R;
Excel:	=ACOS( SIN(lat1)*SIN(lat2) + COS(lat1)*COS(lat2)*COS(lon2-lon1) ) * 6371000
(or with lat/lon in degrees):	=ACOS( SIN(lat1*PI()/180)*SIN(lat2*PI()/180) + COS(lat1*PI()/180)*COS(lat2*PI()/180)*COS(lon2*PI()/180-lon1*PI()/180) ) * 6371000

While simpler, the law of cosines is slightly slower than the haversine, in my tests.

Equirectangular approximation

If performance is an issue and accuracy less important, for small distances Pythagoras’ theorem can be used on an equi­rectangular projec­tion:*

Formula	x = Δλ ⋅ cos φm
	y = Δφ
	d = R ⋅ √x² + y²
JavaScript:	var x = (λ2-λ1) * Math.cos((φ1+φ2)/2); var y = (φ2-φ1); var d = Math.sqrt(x*x + y*y) * R;

This uses just one trig and one sqrt function – as against half-a-dozen trig func­tions for cos law, and 7 trigs + 2 sqrts for haversine. Accuracy is somewhat complex: along meridians there are no errors, otherwise they depend on distance, bearing, and latitude, but are small enough for many purposes* (and often trivial compared with the spherical approxima­tion itself).

Alternatively, the polar coordinate flat-earth formula can be used: using the co-latitudes θ1 = π/2−φ1 and θ2 = π/2−φ2, then d = R ⋅ √θ1² + θ2² − 2 ⋅ θ1 ⋅ θ2 ⋅ cos Δλ. I’ve not compared accuracy.

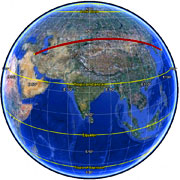Baghdad to Osaka – 
not a constant bearing!

Bearing

In general, your current heading will vary as you follow a great circle path (orthodrome); the final heading will differ from the initial heading by varying degrees according to distance and latitude (if you were to go from say 35°N,45°E (≈ Baghdad) to 35°N,135°E (≈ Osaka), you would start on a heading of 60° and end up on a heading of 120°!).

This formula is for the initial bearing (sometimes referred to as forward azimuth) which if followed in a straight line along a great-circle arc will take you from the start point to the end point:1

Formula:	θ = atan2( sin Δλ ⋅ cos φ2 , cos φ1 ⋅ sin φ2 − sin φ1 ⋅ cos φ2 ⋅ cos Δλ )
where	φ1,λ1 is the start point, φ2,λ2 the end point (Δλ is the difference in longitude)
JavaScript: (all angles  in radians)	var y = Math.sin(λ2-λ1) * Math.cos(φ2); var x = Math.cos(φ1)*Math.sin(φ2) - Math.sin(φ1)*Math.cos(φ2)*Math.cos(λ2-λ1); var brng = Math.atan2(y, x).toDegrees();
Excel: (all angles  in radians)	=ATAN2(COS(lat1)*SIN(lat2)-SIN(lat1)*COS(lat2)*COS(lon2-lon1),         SIN(lon2-lon1)*COS(lat2))  *note that Excel reverses the arguments to ATAN2 – see notes below

Since atan2 returns values in the range -π ... +π (that is, -180° ... +180°), to normalise the result to a compass bearing (in the range 0° ... 360°, with −ve values transformed into the range 180° ... 360°), convert to degrees and then use (θ+360) % 360, where % is (floating point) modulo.

For final bearing, simply take the initial bearing from the end point to the start point and reverse it (using θ = (θ+180) % 360).

Midpoint

This is the half-way point along a great circle path between the two points.1

Formula:	Bx = cos φ2 ⋅ cos Δλ
	By = cos φ2 ⋅ sin Δλ
	φm = atan2( sin φ1 + sin φ2, √(cos φ1 + Bx)² + By² )
	λm = λ1 + atan2(By, cos(φ1)+Bx)
JavaScript: (all angles  in radians)	var Bx = Math.cos(φ2) * Math.cos(λ2-λ1); var By = Math.cos(φ2) * Math.sin(λ2-λ1); var φ3 = Math.atan2(Math.sin(φ1) + Math.sin(φ2), Math.sqrt( (Math.cos(φ1)+Bx)*(Math.cos(φ1)+Bx) + By*By ) ); var λ3 = λ1 + Math.atan2(By, Math.cos(φ1) + Bx);
	The longitude can be normalised to −180…+180 using (lon+540)%360-180

Just as the initial bearing may vary from the final bearing, the midpoint may not be located half-way between latitudes/longitudes; the midpoint between 35°N,45°E and 35°N,135°E is around 45°N,90°E.

Intermediate point

An intermediate point at any fraction along the great circle path between two points can also be calculated.1

Formula:	a = sin((1−f)⋅δ) / sin δ
	b = sin(f⋅δ) / sin δ
	x = a ⋅ cos φ1 ⋅ cos λ1 + b ⋅ cos φ2 ⋅ cos λ2
	y = a ⋅ cos φ1 ⋅ sin λ1 + b ⋅ cos φ2 ⋅ sin λ2
	z = a ⋅ sin φ1 + b ⋅ sin φ2
	φi = atan2(z, √x² + y²)
	λi = atan2(y, x)
where	f is fraction along great circle route (f=0 is point 1, f=1 is point 2), δ is the angular distance d/R between the two points.

 

---

Destination point given distance and bearing from start point

Given a start point, initial bearing, and distance, this will calculate the destina­tion point and final bearing travelling along a (shortest distance) great circle arc.

Destination point along great-circle given distance and bearing from start point

Start point:	,
Bearing:
Distance:	km

Destination point:
Final bearing:
view map

Formula:	φ2 = asin( sin φ1 ⋅ cos δ + cos φ1 ⋅ sin δ ⋅ cos θ )
	λ2 = λ1 + atan2( sin θ ⋅ sin δ ⋅ cos φ1, cos δ − sin φ1 ⋅ sin φ2 )
where	φ is latitude, λ is longitude, θ is the bearing (clockwise from north), δ is the angular distance d/R; d being the distance travelled, R the earth’s radius
JavaScript: (all angles  in radians)	var φ2 = Math.asin( Math.sin(φ1)*Math.cos(d/R) + Math.cos(φ1)*Math.sin(d/R)*Math.cos(brng) ); var λ2 = λ1 + Math.atan2(Math.sin(brng)*Math.sin(d/R)*Math.cos(φ1), Math.cos(d/R)-Math.sin(φ1)*Math.sin(φ2));
	The longitude can be normalised to −180…+180 using (lon+540)%360-180
Excel: (all angles  in radians)	lat2: =ASIN(SIN(lat1)*COS(d/R) + COS(lat1)*SIN(d/R)*COS(brng)) lon2: =lon1 + ATAN2(COS(d/R)-SIN(lat1)*SIN(lat2), SIN(brng)*SIN(d/R)*COS(lat1))  * Remember that Excel reverses the arguments to ATAN2 – see notes below

For final bearing, simply take the initial bearing from the end point to the start point and reverse it with (brng+180)%360.

 

---

Intersection of two paths given start points and bearings

This is a rather more complex calculation than most others on this page, but I've been asked for it a number of times. This comes from Ed William’s aviation formulary. See below for the JavaScript.

Intersection of two great-circle paths

Point 1:	,  Brng 1:
Point 2:	,  Brng 2:

Intersection point:

Formula:	δ12 = 2⋅asin( √(sin²(Δφ/2) + cos φ1 ⋅ cos φ2 ⋅ sin²(Δλ/2)) )
	θa = acos( ( sin φ2 − sin φ1 ⋅ cos δ12 ) / ( sin δ12 ⋅ cos φ1 ) ) θb = acos( ( sin φ1 − sin φ2 ⋅ cos δ12 ) / ( sin δ12 ⋅ cos φ2 ) )	initial / final bearings between points 1 & 2
	if sin(λ2−λ1) > 0     θ12 = θa     θ21 = 2π − θb else     θ12 = 2π − θa     θ21 = θb
	α1 = θ13 − θ12 α2 = θ21 − θ23	angle p2–p1–p3 angle p1–p2–p3
	α3 = acos( −cos α1 ⋅ cos α2 + sin α1 ⋅ sin α2 ⋅ cos δ12 )	angle p1–p2–p3
	δ13 = atan2( sin δ12 ⋅ sin α1 ⋅ sin α2 , cos α2 + cos α1 ⋅ cos α3 )	angular dist. p1–p3
	φ3 = asin( sin φ1 ⋅ cos δ13 + cos φ1 ⋅ sin δ13 ⋅ cos θ13 )	p3 lat
	Δλ13 = atan2( sin θ13 ⋅ sin δ13 ⋅ cos φ1 , cos δ13 − sin φ1 ⋅ sin φ3 )	long p1–p3
	λ3 = λ1 + Δλ13	p3 long
where	φ1, λ1, θ13 : 1st start point & (initial) bearing from 1st point towards intersection point φ2, λ2, θ23 : 2nd start point & (initial) bearing from 2nd point towards intersection point φ3, λ3 : intersection point % = (floating point) modulo
note –	if sin α1 = 0 and sin α2 = 0: infinite solutions if sin α1 ⋅ sin α2 < 0: ambiguous solution this formulation is not always well-conditioned for meridional or equatorial lines

This is a lot simpler using vectors rather than spherical trigonometry: see latlong-vectors.html.

---

Cross-track distance

Here’s a new one: I’ve sometimes been asked about distance of a point from a great-circle path (sometimes called cross track error).

Formula:	dxt = asin( sin(δ13) ⋅ sin(θ13−θ12) ) ⋅ R
where	δ13 is (angular) distance from start point to third point θ13 is (initial) bearing from start point to third point θ12 is (initial) bearing from start point to end point R is the earth’s radius
JavaScript:	var dXt = Math.asin(Math.sin(d13/R)*Math.sin(θ13-θ12)) * R;

Here, the great-circle path is identified by a start point and an end point – depending on what initial data you’re working from, you can use the formulæ above to obtain the relevant distance and bearings. The sign of dxt tells you which side of the path the third point is on.

The along-track distance, from the start point to the closest point on the path to the third point, is

Formula:	dat = acos( cos(δ13) / cos(δxt) ) ⋅ R
where	δ13 is (angular) distance from start point to third point δxt is (angular) cross-track distance R is the earth’s radius
JavaScript:	var dAt = Math.acos(Math.cos(d13/R)/Math.cos(dXt/R)) * R;

Closest point to the poles

And: ‘Clairaut’s formula’ will give you the maximum latitude of a great circle path, given a bearing θ and latitude φ on the great circle:

Formula:	φmax = acos( | sin θ ⋅ cos φ | )
JavaScript:	var φMax = Math.acos(Math.abs(Math.sin(θ)*Math.cos(φ)));

 

---

Rhumb lines

A ‘rhumb line’ (or loxodrome) is a path of constant bearing, which crosses all meridians at the same angle.

Sailors used to (and sometimes still) navigate along rhumb lines since it is easier to follow a constant compass bearing than to be continually adjusting the bearing, as is needed to follow a great circle. Rhumb lines are straight lines on a Mercator Projec­tion map (also helpful for naviga­tion).

Rhumb lines are generally longer than great-circle (orthodrome) routes. For instance, London to New York is 4% longer along a rhumb line than along a great circle – important for avia­tion fuel, but not particularly to sailing vessels. New York to Beijing – close to the most extreme example possible (though not sailable!) – is 30% longer along a rhumb line.

Rhumb-line distance between two points

Point 1:	,
Point 2:	,

Distance:	km
Bearing:
Midpoint:
view map

Destination point along rhumb line given distance and bearing from start point

Start point:	,
Bearing:
Distance:	km

Destination point:
view map

 

Key to calculations of rhumb lines is the inverse Gudermannian func­tion¹, which gives the height on a Mercator projec­tion map of a given latitude: ln(tanφ + secφ) or ln( tan(π/4+φ/2) ). This of course tends to infinity at the poles (in keeping with the Mercator projec­tion). For obsessives, there is even an ellipsoidal version, the ‘isometric latitude’: ψ = ln( tan(π/4+φ/2) / [ (1−e⋅sinφ) / (1+e⋅sinφ) ]e/2), or its better-conditioned equivalent ψ = atanh(sinφ) − e⋅atanh(e⋅sinφ).

The formulæ to derive Mercator projection easting and northing coordinates from spherical latitude and longitude are then¹

	E = R ⋅ λ
	N = R ⋅ ln( tan(π/4 + φ/2) )

The following formulæ are from Ed Williams’ aviation formulary.¹

Distance

Since a rhumb line is a straight line on a Mercator projec­tion, the distance between two points along a rhumb line is the length of that line (by Pythagoras); but the distor­tion of the projec­tion needs to be compensated for.

On a constant latitude course (travelling east-west), this compensa­tion is simply cosφ; in the general case, it is Δφ/Δψwhere Δψ = ln( tan(π/4 + φ2/2) / tan(π/4 + φ1/2) ) (the ‘projected’ latitude difference)

Formula:	Δψ = ln( tan(π/4 + φ2/2) / tan(π/4 + φ1/2) )	(‘projected’ latitude difference)
	q = Δφ/Δψ (or cosφ for E-W line)
	d = √(Δφ² + q²⋅Δλ²) ⋅ R	(Pythagoras)
where	φ is latitude, λ is longitude, Δλ is taking shortest route (<180°), R is the earth’s radius, ln is natural log
JavaScript: (all angles  in radians)	var Δψ = Math.log(Math.tan(Math.PI/4+φ2/2)/Math.tan(Math.PI/4+φ1/2)); var q = Math.abs(Δψ) > 10e-12 ? Δφ/Δψ : Math.cos(φ1); // E-W course becomes ill-conditioned with 0/0 // if dLon over 180° take shorter rhumb line across the anti-meridian: if (Math.abs(Δλ) > Math.PI) Δλ = Δλ>0 ? -(2*Math.PI-Δλ) : (2*Math.PI+Δλ); var dist = Math.sqrt(Δφ*Δφ + q*q*Δλ*Δλ) * R;

Bearing

A rhumb line is a straight line on a Mercator projection, with an angle on the projec­tion equal to the compass bearing.

Formula:	Δψ = ln( tan(π/4 + φ2/2) / tan(π/4 + φ1/2) )	(‘projected’ latitude difference)
	θ = atan2(Δλ, Δψ)
where	φ is latitude, λ is longitude, Δλ is taking shortest route (<180°), R is the earth’s radius, ln is natural log
JavaScript: (all angles  in radians)	var Δψ = Math.log(Math.tan(Math.PI/4+φ2/2)/Math.tan(Math.PI/4+φ1/2)); // if dLon over 180° take shorter rhumb line across the anti-meridian: if (Math.abs(Δλ) > Math.PI) Δλ = Δλ>0 ? -(2*Math.PI-Δλ) : (2*Math.PI+Δλ); var brng = Math.atan2(Δλ, Δψ).toDegrees();

Destination

Given a start point and a distance d along constant bearing θ, this will calculate the destina­tion point. If you maintain a constant bearing along a rhumb line, you will gradually spiral in towards one of the poles.

Formula:	δ = d/R	(angular distance)
	Δψ = ln( tan(π/4 + φ2/2) / tan(π/4 + φ1/2) )	(‘projected’ latitude difference)
	q = Δφ/Δψ (or cos φ for E-W line)
	Δλ = δ ⋅ sin θ / q
	φ2 = φ1 + δ ⋅ cos θ
	λ2 = λ1 + Δλ
where	φ is latitude, λ is longitude, Δλ is taking shortest route (<180°), ln is natural log, R is the earth’s radius
JavaScript: (all angles  in radians)	var Δφ = δ*Math.cos(θ); var φ2 = φ1 + Δλ; var Δψ = Math.log(Math.tan(φ2/2+Math.PI/4)/Math.tan(φ1/2+Math.PI/4)); var q = Math.abs(Δψ) > 10e-12 ? Δφ / Δψ : Math.cos(φ1); // E-W course becomes ill-conditioned with 0/0 var Δλ = δ*Math.sin(θ)/q; var λ2 = λ1 + Δλ; // check for some daft bugger going past the pole, normalise latitude if so if (Math.abs(φ2) > Math.PI/2) φ2 = φ2>0 ? Math.PI-φ2 : -Math.PI-φ2;
	The longitude can be normalised to −180…+180 using (lon+540)%360-180

Mid-point

This formula for calculating the ‘loxodromic midpoint’, the point half-way along a rhumb line between two points, is due to Robert Hill and Clive Tooth1 (thx Axel!).

Formula:	φm = (φ1+φ2) / 2
	f1 = tan(π/4 + φ1/2)
	f2 = tan(π/4 + φ2/2)
	fm = tan(π/4+φm/2)
	λm = [ (λ2−λ1) ⋅ ln(fm) + λ1 ⋅ ln(f2) − λ2 ⋅ ln(f1) ] / ln(f2/f1)
where	φ is latitude, λ is longitude, ln is natural log
JavaScript: (all angles  in radians)	if (Math.abs(λ2-λ1) > Math.PI) λ1 += 2*Math.PI; // crossing anti-meridian var φ3 = (φ1+φ2)/2; var f1 = Math.tan(Math.PI/4 + φ1/2); var f2 = Math.tan(Math.PI/4 + φ2/2); var f3 = Math.tan(Math.PI/4 + φ3/2); var λ3 = ( (λ2-λ1)*Math.log(f3) + λ1*Math.log(f2) - λ2*Math.log(f1) ) / Math.log(f2/f1); if (!isFinite(λ3)) λ3 = (λ1+λ2)/2; // parallel of latitude
	The longitude can be normalised to −180…+180 using (lon+540)%360-180

---

Using the scripts in web pages

Using these scripts in web pages would be something like the following:

<script src="latlon.js">/* Latitude/Longitude formulae */</script>
<script src="dms.js">/* Geodesy representation conversions */</script>
...
<form>
  Lat1: <input type="text" name="lat1" id="lat1"> Lon1: <input type="text" name="lon1" id="lon1">
  Lat2: <input type="text" name="lat2" id="lat2"> Lon2: <input type="text" name="lon2" id="lon2">
  <button onClick="var p1 = LatLon(Dms.parseDMS(f.lat1.value), Dms.parseDMS(f.lon1.value));
                   var p2 = LatLon(Dms.parseDMS(f.lat2.value), Dms.parseDMS(f.lon2.value));
                   alert(p1.distanceTo(p2));">Calculate distance</button>
</form>

If you use jQuery, the code can be separated from the HTML:

<script src="//code.jquery.com/jquery-3.0.0.min.js"></script>
<script src="latlon.js">/* Latitude/Longitude formulae */</script>
<script src="dms.js">/* Geodesy representation conversions */</script>
<script>
  document.addEventListener('DOMContentLoaded', function(event) {
    $('#calc-dist').click(function() {
      var p1 = LatLon(Dms.parseDMS($('#lat1').val()), Dms.parseDMS($('#lon1').val()));
      var p2 = LatLon(Dms.parseDMS($('#lat2').val()), Dms.parseDMS($('#lon2').val()));
      $('#result-distance').html(p1.distanceTo(p2));
    });
  });
</script>
...
<form>
  Lat1: <input type="text" name="lat1" id="lat1"> Lon1: <input type="text" name="lon1" id="lon1">
  Lat2: <input type="text" name="lat2" id="lat2"> Lon2: <input type="text" name="lon2" id="lon2">
  <button id="calc-dist">Calculate distance</button>
  <output id="result-distance"></output> km
</form>

---

Convert between degrees-minutes-seconds & decimal degrees

Latitude	Longitude
		1° ≈ 111 km (110.57 eq’l — 111.70 polar)
		1′ ≈ 1.85 km (= 1 nm)	0.01° ≈ 1.11 km
		1″ ≈ 30.9 m	0.0001° ≈ 11.1 m

Display calculation results as:  degrees  deg/min  deg/min/sec

---

Notes:

• Accuracy: since the earth is not quite a sphere, there are small errors in using spherical geometry; the earth is actually roughly ellipsoidal (or more precisely, oblate spheroidal) with a radius varying between about 6,378km (equatorial) and 6,357km (polar), and local radius of curvature varying from 6,336km (equatorial meridian) to 6,399km (polar). 6,371 km is the generally accepted value for the earth’s mean radius. This means that errors from assuming spherical geometry might be up to 0.55% crossing the equator, though generally below 0.3%, depending on latitude and direction of travel (whuber explores this in excellent detail on stackexchange). An accuracy of better than 3m in 1km is mostly good enough for me, but if you want greater accuracy, you could use the Vincenty formula for calculating geodesic distances on ellipsoids, which gives results accurate to within 1mm. (Out of sheer perversity – I’ve never needed such accuracy – I looked up this formula and discovered the JavaScript implementation was simpler than I expected).
• Trig functions take arguments in radians, so latitude, longitude, and bearings in degrees (either decimal or degrees/minutes/seconds) need to be converted to radians, rad = π.deg/180. When converting radians back to degrees (deg = 180.rad/π), West is negative if using signed decimal degrees. For bearings, values in the range -π to +π [-180° to +180°] need to be converted to 0 to +2π [0°–360°]; this can be done by (brng+2.π)%2.π [or brng+360)%360] where % is the (floating point) modulo operator (note that different languages implement themodulo operation in different ways).
• All bearings are with respect to true north, 0°=N, 90°=E, etc; if you are working from a compass, magnetic north varies from true north in a complex way around the earth, and the difference has to be compensated for by variances indicated on local maps.
• The atan2() function widely used here takes two arguments, atan2(y, x), and computes the arc tangent of the ratio y/x. It is more flexible than atan(y/x), since it handles x=0, and it also returns values in all 4 quadrants -π to +π (the atan function returns values in the range -π/2 to +π/2).
• If you implement any formula involving atan2 in a spreadsheet (Microsoft Excel, LibreOffice Calc, Google Sheets, Apple Numbers), you will need to reverse the arguments, as Excel etc have them the opposite way around fromJavaScript – conventional order is atan2(y, x), but Excel uses atan2(x, y). To use atan2 in a (VBA) macro, you can use WorksheetFunction.Atan2().
• If you are using Google Maps, several of these functions are now provided in the Google Maps API V3 ‘spherical’ library (computeDistanceBetween(), computeHeading(), computeOffset(), interpolate(), etc; note they use a default Earth radius of 6,378,137 meters).
• If you use UK Ordnance Survey Grid References, I have implemented a script for converting between Lat/Long & OS Grid References.
• If you use UTM coordinates or MGRS grid references, I have implemented scripts for converting between Lat/Long, UTM, & MGRS.
• I learned a lot from the US Census Bureau GIS FAQ which is no longer available, so I’ve made a copy.
• Thanks to Ed Williams’ Aviation Formulary for many of the formulæ.
• For miles, divide km by 1.609344
• For nautical miles, divide km by 1.852

---

See below for the JavaScript source code, also available on GitHub. Note I use Greek letters in variables representing maths symbols conventionally presented as Greek letters: I value the great benefit in legibility over the minor inconvenience in typing (if you encounter any problems, ensure your <head> includes <meta charset="utf-8">).

With its untyped C-style syntax, JavaScript reads remarkably close to pseudo-code: exposing the algorithms with a minimum of syntactic distractions. These functions should be simple to translate into other languages if required, though can also be used as-is in browsers and Node.js.

I have extended the base JavaScript Number object with toRadians() and toDegrees() methods: I don’t see great likelihood of conflicts, as these are ubiquitous operations.

I also have a page illustrating the use of the spherical law of cosines for selecting points from a database within a specified bounding circle – the example is based on MySQL+PDO, but should be extensible to other DBMS platforms.

Several people have asked about example Excel spreadsheets, so I have implemented the distance & bearing and thedestination point formulæ as spreadsheets, in a form which breaks down the all stages involved to illustrate the operation.

January 2010: I have revised the scripts to be structured as methods of a LatLon object. Of course, while JavaScript isobject-oriented, it is a prototype-based rather than class-based language, so this is not actually a class, but isolating code into a separate namespace is good JavaScript practice. If you’re not familiar with JavaScript syntax,LatLon.prototype.distanceTo = function(point) { ... }, for instance, defines a ‘distanceTo’ method of the LatLonobject (/class) which takes a LatLon object as a parameter (and returns a number). The Dms namespace acts as a static class for geodesy formatting / parsing / conversion functions.

January 2015: I have refactored the scripts to inter-operate better, and rationalised certain aspects: the JavaScript file is now latlon-spherical.js instead of simply latlon.js; distances are now always in metres; the earth’s radius is now a parameter to distance calculation methods rather than to the constructor; the previous Geo object is now Dms, to better indicate its purpose; the destinationPoint function has the distance parameter before the bearing.

Performance: as noted above, the haversine distance calculation takes around 2 – 5 micro­seconds (hence around 200,000 – 500,000 per second). I have yet to complete timing tests on other calculations.

Other languages: I cannot support translations into other languages, but if you have ported the code to another language, I am happy to provide links here.

• Brian Lambert has made an Objective-C version.
• Jean Brouwers has made a Python version.

I offer these scripts for free use and adaptation to balance my debt to the open-source info-verse. You are welcome to re-use these scripts [under an MIT licence, without any warranty express or implied] provided solely that you retain my copyright notice and a link to this page.

If you would like to show your appreciation and support continued development of these scripts, I would most gratefully accept donations.

If you need any advice or development work done, I am available for consultancy.

If you have any queries or find any problems, contact me at ku.oc.epyt-elbavom@oeg-stpircs.

© 2002-2017 Chris Veness