通过阶乘的例子,练习在JavaScript, Scala和ABAP里实现尾递归

Before we start to research tail recursion, let’s first have a look at the normal recursion.

A simple factorial implementation by recursion:

function factorial(n){
  if(n ===1) {
     return 1;
  }
  return n *factorial(n -1);
}

Let N = 5, see how new stack frame is created for each time of recursive call:

 

 

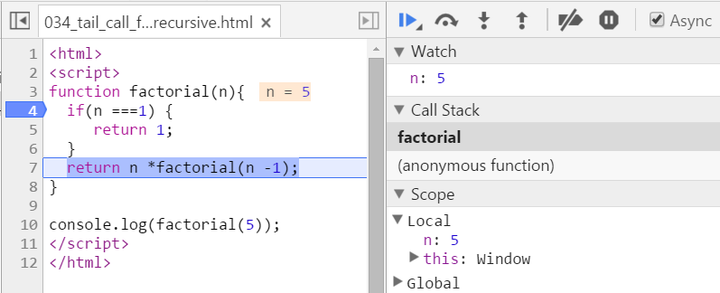
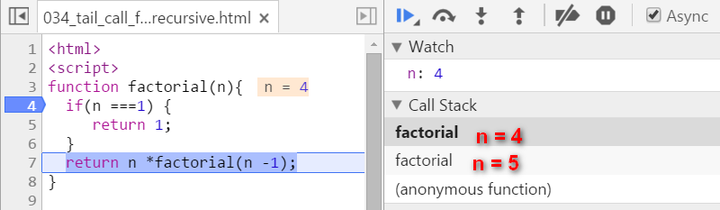
We have two stack frames now, one stores the context when n = 5, and the topmost one for current calculation: n = 4

 

 

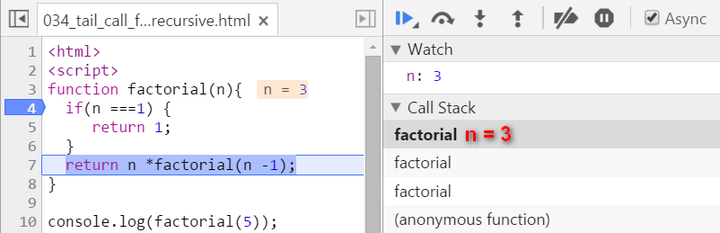
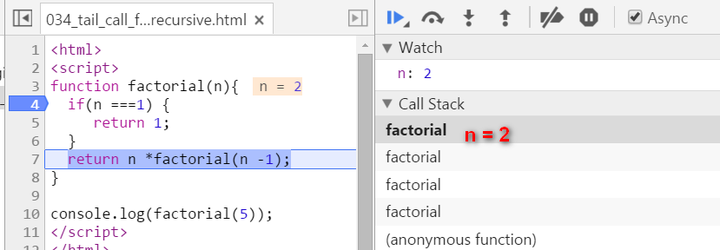
Now since n equals to 1, we stop recursion. The current stack frame ( n = 1 ) will be poped up, the frame under it will be activated and become the topmost frame, with calculated result 1 passed into.

 

 

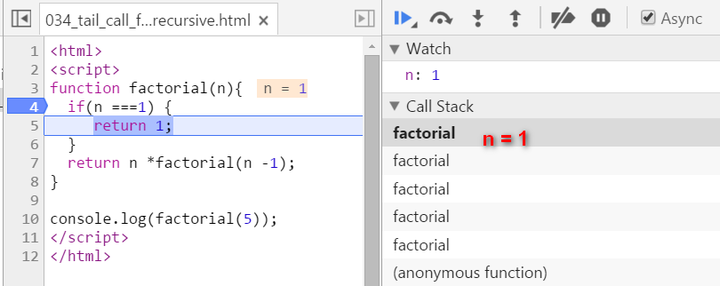
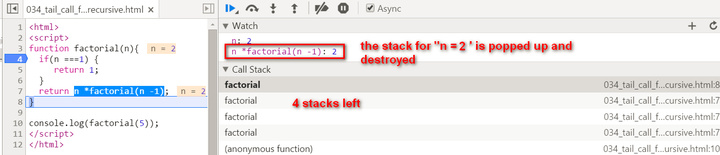
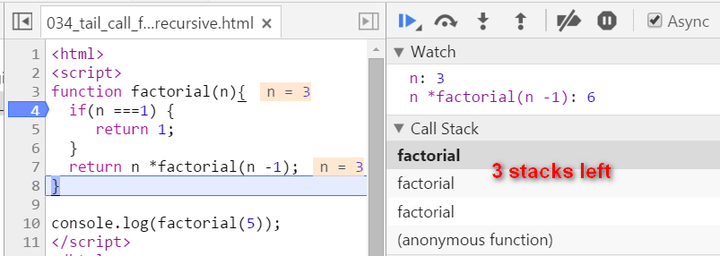
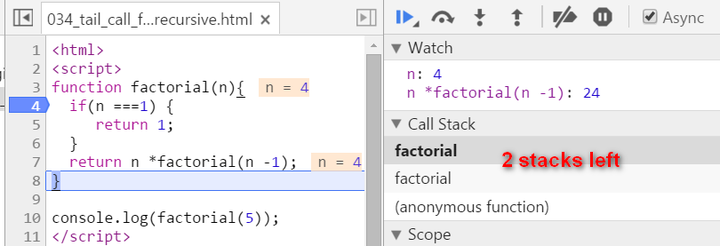
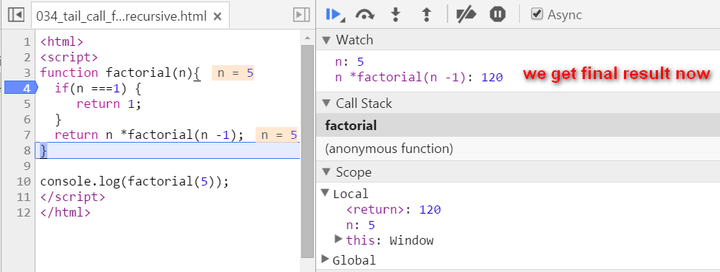
key note for normal recursion: during recursion, every generated stack frame is needed and could not e destroyed until the final result is calculated. The calculation is actually not started until the recursion reaches the end ( the condition n === 1 fulfills ). If N is a big integer, it will lead to huge number of stack frames and finally the “stack overflow” or “out of memory” is inevitable.

tail recursion

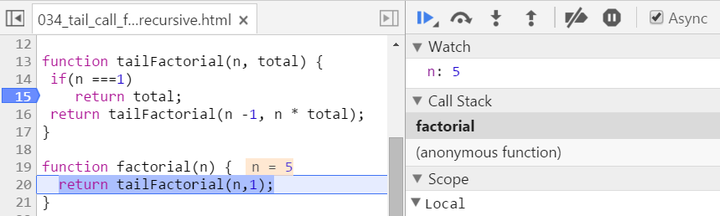
Source code below:

function tailFactorial(n, total) {
if(n ===1)
    return total;
return tailFactorial(n -1, n * total);
}
function factorial2(n) {
  return tailFactorial(n,1);
}

There are two biggest differences compared with normal recursion:

(1) A new internal function tailFactorial is introduced here.

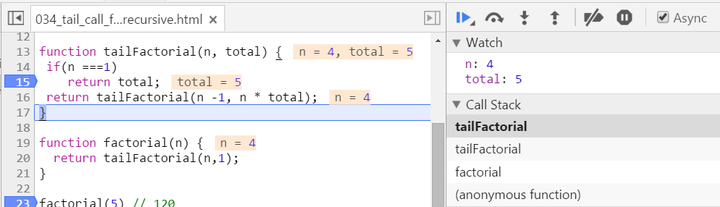
(2) The calculation is actually now spread within every recursive stack frame. Each frame finishes one part of calculation and pass the current result to the next frame. Once the current stack frame finishes its task, it is actually not needed any more. And thus for example the model browser can then do some optimization on those useless stack frames.

Observe the stack frame for tail recursion step by step:

 

 

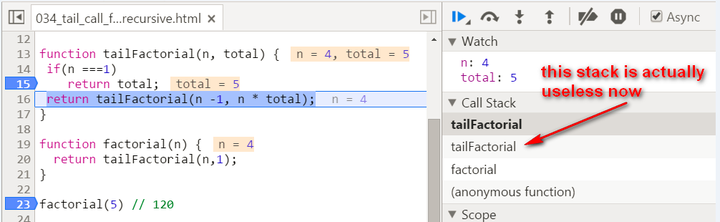
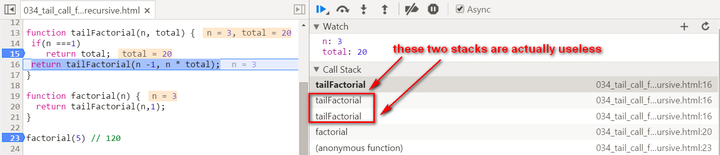
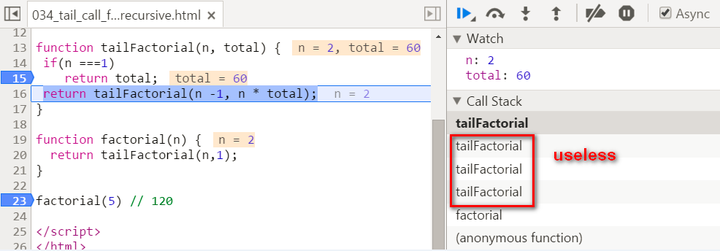
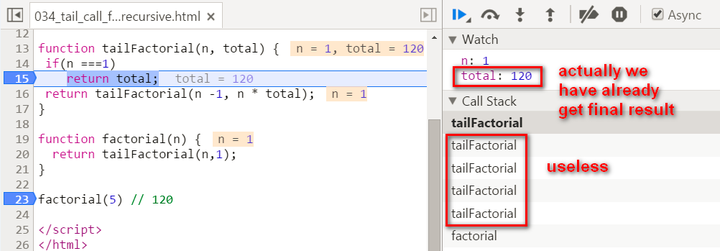
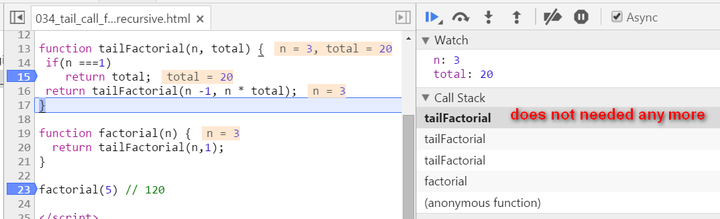
stack popped up:

 

 

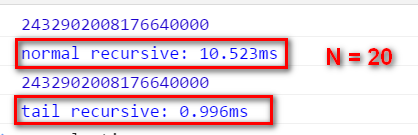
When N = 20, the tail recursion has a far better performance than the normal recursion:

 

 

Update 2016-01-11

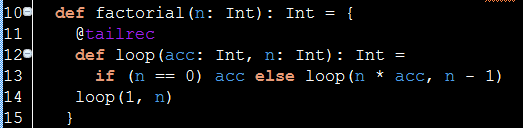
Tail recursion implementation via Scala:

 

 

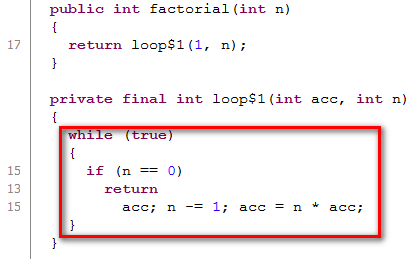
The interesting thing is, after the Scala code is compiled into Java Byte code, compiler will eliminate the recursion automatically:

 

 

Tail Recursion in ABAP

First this is the normal recursion:

REPORT zrecursion.

START-OF-SELECTION.

  DATA: lv_result TYPE int4.

  PERFORM fac USING 6 CHANGING lv_result.

  WRITE: / lv_result.

FORM fac USING iv_n TYPE int4 CHANGING cv_result TYPE int4.
  DATA: lv_n TYPE i.

  cv_result = lv_n = iv_n.
  lv_n = lv_n - 1.
  IF lv_n > 1.
    PERFORM fac USING lv_n CHANGING cv_result.
  ENDIF.
  IF lv_n = 1.
    cv_result = cv_result * lv_n.
  ELSE.
    cv_result = cv_result * iv_n.
  ENDIF.
ENDFORM.

And here comes tail recursion version:

REPORT ztail.

START-OF-SELECTION.

  DATA: lv_result TYPE int4.

  PERFORM fac USING 5 1 CHANGING lv_result.

  WRITE: / lv_result.

FORM fac USING iv_n TYPE int4 iv_acc TYPE int4 CHANGING cv_result TYPE int4.
  DATA: lv_n          TYPE i,
        lv_accumulate TYPE i.

  IF iv_n < 1.
    cv_result = 1.
  ELSEIF iv_n = 1.
    cv_result = iv_acc * iv_n.
  ELSEIF iv_n > 1.
    lv_n = iv_n - 1.
    lv_accumulate = iv_acc * iv_n.
    PERFORM fac USING lv_n lv_accumulate CHANGING cv_result.
  ENDIF.
ENDFORM.

要获取更多Jerry的原创文章，请关注公众号"汪子熙":