前段时间,从微薄上得到了一个开源电子书:
下载下来看了一下,发现该书讲的数据挖掘算法浅显易懂,受益匪浅,不敢独享,特将我的理解+精简翻译奉上:
1.1. 共同爱好——我喜欢你所喜欢的。
我们从学习推荐系统来开始数据挖掘之旅,推荐系统到处可见,国外的amazon,国内的京东、淘宝等系统。
如何理解推荐系统呢?我们看一个例子:
例如我们在京东浏览一本《数据挖掘概念与技术》:

从页面向下看:

滚动到页面的最下方,可以看到:

京东根据我们说浏览的图书,自动为我们推荐了一些相关的书籍。
推荐系统就是所谓的协同过滤(collaborative filtering),之所以叫协同,是因为得到推荐结果,是大家的力量——从众多用户那里搜集到信息,从中得到推荐信息。
基于用户的推荐——当系统发现你购买了一本《数据挖掘概念与技术》,而有其他用户同时购买了《数据挖掘概念与技术》和《mongobd权威指南》,那么系统猜想你同时喜欢《mongobd权威指南》的可能性也很大,就会把《mongobd权威指南》推荐给你。这种推荐是依据用户相似性,即两个用户有相同的爱好做出的推荐。
基于项目的推荐——将相同类型的东西推荐给用户,如上面的京东推荐的最佳组合就是基于项目的推荐。
首先来看看基于用户的推荐。
1.2. 如何发现两个人具有相似性?
还以图书为例,假设用户对amazon网站的图书进行了评价,从1星到5星,评价从差到好。评价结果如下表:
|
用户 书名
|
Snow Crash
|
Girl with the
Dragon Tattoo
|
|
Amy
|
5
|
5
|
|
Bill
|
2
|
5
|
|
Jim
|
1
|
4
|
将结果描述在二维图上:

从图上可以形象的看出:Bill和Jim距离较近。
现在有X先生,他给snow crash打了4星,给dragon tattoo 2星,我们为他推荐什么书籍呢?第一步就是要判断一下X和谁的爱好更相似。

1.2.1. Manhattan Distance——曼哈顿距离
最简单的距离计算方法就是曼哈顿距离,在二维图上,点Amy的坐标是(x1,y1),X的坐标是(x2,y2),那么amy和X之间的曼哈顿距离就是:
|x1-x2|+|y1-y2|。
则X到三个人的曼哈顿距离是:
|
|
到X的曼哈顿距离
|
|
Amy
|
4
|
|
Bill
|
5
|
|
Jim
|
6
|
Amy是最近的,从图上也可以看出。那么如果Amy喜欢《The windup girl》,那么我们就把这本书推荐给X先生。
曼哈顿距离的优点是计算速度快,单过于简单。
1.2.2. EuclideanDistance——欧几里得距离
欧几里得距离是根据毕达哥拉斯定律得到的,至于该定律,想必大家都学过的,就不再多说了。
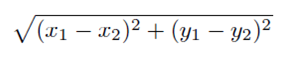
重新计算三个点到X的欧几里得距离:
|
|
到X的欧几里得距离
|
|
Amy
|
3.16
|
|
Bill
|
3.61
|
|
Jim
|
3.61
|
1.2.3. N维扩展
实际情况中,用户可能不止给两本书打分,而是多个,这样就把距离的计算从二维空间推广到了N维空间,当然计算方法是不变的。
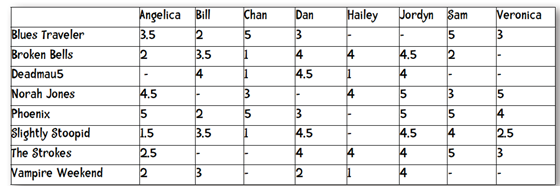
计算距离的时候,我们只计算共同项,即标有-标记的书不在计算项目中。
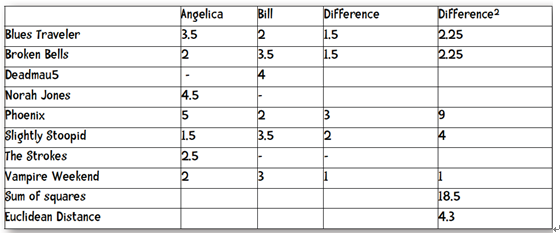
动手:
1. 计算一下Hailey和Veronica之间的欧氏距离。
2. 计算一下Hailey和Jordyn之间的欧氏距离。
答案:

缺陷:从上两题中看出,Hailey和Veronica只有两个共同项,但是他们之间的距离却是1.414,而Hailey和Jordyn之间有5项相同,之间的距离是4.387。很明显,Hailey和Jordyn之间更相似,但是欧氏距离却更大。这就说明该算法有缺陷。当计算的共同项较多时,计算的距离值可信度就更高。
1.2.4. 算法泛化
1.2.5. Minkowski距离算法
从曼哈顿距离和欧几里得距离的计算公式,可以推演出所谓的Minkowski距离算法:

当r=1时,就是曼哈顿距离;
当r=2时,就是欧几里得距离;
当r=∞时,就是无上界距离。
1.3. 算法代码实现
基于用户的推荐算法流程:
本文中,使用python来实现以上算法。
准备数据:
将表中的数据使用python的dict存储起来:
users = {"Angelica": {"Blues Traveler": 3.5, "Broken Bells": 2.0, "Norah Jones": 4.5, "Phoenix": 5.0, "Slightly Stoopid": 1.5, "The Strokes": 2.5, "Vampire Weekend": 2.0},
"Bill":{"Blues Traveler": 2.0, "Broken Bells": 3.5, "Deadmau5": 4.0, "Phoenix": 2.0, "Slightly Stoopid": 3.5, "Vampire Weekend": 3.0},
"Chan": {"Blues Traveler": 5.0, "Broken Bells": 1.0, "Deadmau5": 1.0, "Norah Jones": 3.0, "Phoenix": 5, "Slightly Stoopid": 1.0},
"Dan": {"Blues Traveler": 3.0, "Broken Bells": 4.0, "Deadmau5": 4.5, "Phoenix": 3.0, "Slightly Stoopid": 4.5, "The Strokes": 4.0, "Vampire Weekend": 2.0},
"Hailey": {"Broken Bells": 4.0, "Deadmau5": 1.0, "Norah Jones": 4.0, "The Strokes": 4.0, "Vampire Weekend": 1.0},
"Jordyn": {"Broken Bells": 4.5, "Deadmau5": 4.0, "Norah Jones": 5.0, "Phoenix": 5.0, "Slightly Stoopid": 4.5, "The Strokes": 4.0, "Vampire Weekend": 4.0},
"Sam": {"Blues Traveler": 5.0, "Broken Bells": 2.0, "Norah Jones": 3.0, "Phoenix": 5.0, "Slightly Stoopid": 4.0, "The Strokes": 5.0},
"Veronica": {"Blues Traveler": 3.0, "Norah Jones": 5.0, "Phoenix": 4.0, "Slightly Stoopid": 2.5, "The Strokes": 3.0}
}
测试一下
>>> users["Veronica"]
>>>{'The Strokes': 3.0, 'Slightly Stoopid': 2.5, 'Norah Jones': 5.0, 'Phoenix': 4.0,
'Blues Traveler': 3.0}
>>>
1.3.1. 曼哈顿距离算法:
def manhattan(rate1,rate2):
distance = 0
commonRating = False
for key in rate1:
if key in rate2:
distance+=abs(rate1[key]-rate2[key])
commonRating=True
if commonRating:
return distance
else:
return -1
测试算法:
>>> manhattan(users['Hailey'], users['Veronica'])
2.0
>>> manhattan(users['Hailey'], users['Jordyn'])
1.5
>>>
算法:找到距离最近的用户列表。
1.3.2. 返回最近距离用户
def computeNearestNeighbor(username,users):
distances = []
for key in users:
if key<>username:
distance = manhattan(users[username],users[key])
distances.append((distance,key))
distances.sort()
return distances
测试:
>>> computeNearestNeighbor('Hailey', users)
[(2.0, 'Veronica'), (4.0, 'Chan'),(4.0, 'Sam'), (4.5, 'Dan'), (5.0, 'Angelica'),
(5.5, 'Bill'), (7.5, 'Jordyn')]
>>>
#推荐
def recommend(username,users):
#获得最近用户的name
nearest = computeNearestNeighbor(username,users)[0][1]
recommendations =[]
#得到最近用户的推荐列表
neighborRatings = users[nearest]
for key in neighborRatings:
if not key in users[username]:
recommendations.append((key,neighborRatings[key]))
#排序
recommendations.sort(key=lambda rat:rat[1], reverse=True)
return recommendations
测试:
>>> recommend('Hailey', users)
[('Phoenix', 4.0), ('Blues Traveler', 3.0), ('Slightly Stoopid', 2.5)]
>>> recommend('Chan', users)
[('The Strokes', 4.0), ('Vampire Weekend', 1.0)]
>>> recommend('Sam', users)
[('Deadmau5', 1.0)]
Ok ,一个简单的推荐算法就完成了。
练习3:
实现一个Minkowski距离算法:

答案:
03 |
def minkowski(rate1,rate2,r):
|
13 |
distance+=pow(abs(rate1[key]-rate2[key]),r)
|
19 |
return pow(distance,1/r)
|
练习4:
用Minkowski算法计算computeNearestNeighbor中的欧几里得距离。
答案:
def minkowski(rate1,rate2,r):
distance = 0
commonRating = False
for key in rate1:
if key in rate2:
distance+=pow(abs(rate1[key]-rate2[key]),r)
commonRating=True
if commonRating:
return pow(distance,1/r)
else:
return -1
1.3.4. 培生相关系数
用户具有偏见性,如Bill打分在2-4之间,而Hailey打分只有1和4.Jordyn打分只有4和5,那么bill打的4分和Jordyn的4分是一样的评价吗?显然不是,但是计算的时候,算法是无法判断的。因此需要降低这种主观带来的影响。所以就有了新的算法。
培生相关系数:Pearson Correlation Coefficient。
培生相关系数是测量两个变量之间的相关性的数值,其范围是从-1到1之间。1表示完全一致,-1表示不一致。与距离算法相反,培生相关稀疏越大越好。
算法:
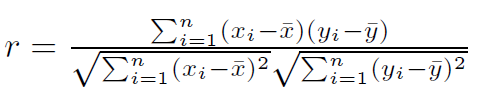
由于该公式较难实现,有了以下近似算法:

上面的公式看似复杂,很吓人,不过可以一一分解:
例如我们计算Angelica 和 Bill之间的培生相关系数:
 那么分子就是70-67.5=2.5
那么分子就是70-67.5=2.5
再来计算分母:

由此可以看到,两者的是完全相关的。
练习5:实现培生相关系数算法
以下是测试结果,用来测试你的算法正确性。
>>> pearson(users['Angelica'], users['Bill'])
-0.90405349906826993
>>> pearson(users['Angelica'], users['Hailey'])
0.42008402520840293
>>> pearson(users['Angelica'], users['Jordyn'])
0.76397486054754316
>>>
答案:
def pearson(rate1,rate2):
sum_xy = 0
sum_x=0
sum_y=0
sum_x2=0
sum_y2=0
n=0
for key in rate1:
if key in rate2:
n+=1
x=rate1[key]
y=rate2[key]
sum_xy += x*y
sum_x +=x
sum_y +=y
sum_x2 +=x*x
sum_y2 +=y*y
#计算距离
if n==0:
return 0
else:
sx=sqrt(sum_x2-(pow(sum_x,2)/n))
sy=sqrt(sum_y2-(pow(sum_y,2)/n))
if sx<>0 and sy<>0:
denominator=(sum_xy-sum_x*sum_y/n)/sx/sy
else:
denominator=0
return denominator
练习6:使用培生相关系数替代距离算法,实现简单推荐系统。
1.3.5. 余弦相似性
 从上表中,我们可以凭感觉:Sally与Ann更相似。如何用算法实现上述描述呢?
从上表中,我们可以凭感觉:Sally与Ann更相似。如何用算法实现上述描述呢?
余弦相似性算法:
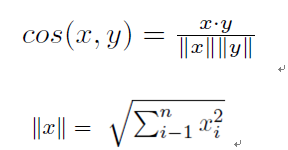
余弦相似性的值范围从-1到1,值越大表示相似性越高。
练习7:实现余弦相似性算法,并改造我们的推荐算法。
1.4. 不同算法的适用情况
1. 如果数据比较稠密(即数据中的空项很少),那么适用距离算法如欧几里得距离等较合适。
2. 如果数据的差异较大(即不同用户的数据差别较大),Pearson算法较合适。
3. 数据稀疏,余弦相关性算法较合适。
1.5. 弱点
单纯的基于用户的推荐系统是有缺陷的,例如推荐系统计算得到王五和张三最相似,王五其实一点也不喜欢张学友,而张三是张学友家亲戚,当然,张三非常喜欢张学友咯。那么推荐系统会把张学友推荐给张三,实际情况适得其反。
仔细分析一下,主要原因是因为我们把希望全寄托在了这个最相似的用户身上。如果多考虑几个相似的用户的喜好,推荐的效果会更好。因此提出了k-nearest neighbor 算法。
k-nearest neighbor 算法中的k表示与目标用户最相似的k个用户。例如我们使用pearson算法,得到Ann最相似的三个用户及值:

根据pearson值,计算三个用户所占的权重:
Sally:0.8/(.08+0.7+0.5)=0.4
……

三个人对Grey Wardens的打分:
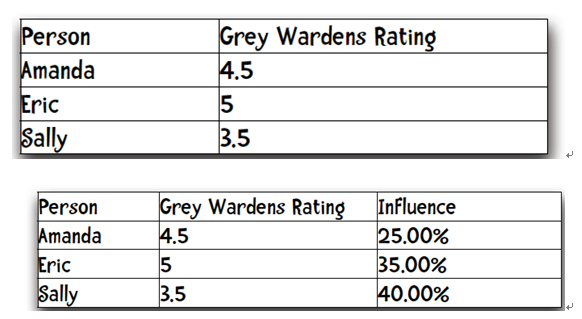
综合得到Ann对Grey Wardens的打分:
Projected rating = (4.5 x 0.25) + (5 x 0.35) + (3.5 x 0.4)= 4.275
练习8:将pearson算法改造为k-nearest neighbor
本文算法全部代码见附件
下一部分:基于项目的推荐算法,slope-one算法




















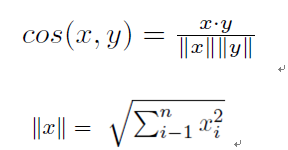






相关推荐
音乐个性化推荐——基于ALS矩阵分解的协同过滤算法 协同过滤算法(Collaborative Filtering)是一种经典的推荐算法,其基本原理是“协同大家的反馈、评价和意见,一起对海量的信息进行过滤,从中筛选出用户可能感...
【基于用户协同过滤算法代码实现Java】 用户协同过滤(User-Based Collaborative Filtering,简称UCF)是一种常用的推荐系统算法,其基本思想是:如果两个用户在过去对某些项目有相似的评分,那么他们可能会对未...
基于物品的协同过滤则侧重于找到物品之间的相似性,通过推荐用户尚未体验但与他们已喜欢的物品相似的物品来实现个性化推荐。 在电影推荐系统中,协同过滤算法可以这样工作: 1. 数据收集:首先,系统需要收集大量...
华中科技大学的一群学生通过创新创业项目的实践,将协同过滤算法应用于食堂菜品智能推荐程序的设计中,成功开发了基于微信小程序的菜品推荐评测系统,这不仅解决了传统菜品评测软件的不足,还为用户提供了个性化、...
基于python与协同过滤算法的电影推荐系统设计与实现
在本项目中,我们将关注一种常见的推荐系统算法——协同过滤(Collaborative Filtering, CF),以及如何使用Java语言来实现这一算法。 **协同过滤原理** 协同过滤分为用户-用户协同过滤(User-Based CF)和物品-...
在本项目实践中,我们聚焦于人工智能领域中的一个关键应用——推荐算法,具体是利用豆瓣电影用户数据,通过Canopy预处理以及K-means聚类来实现协同过滤推荐算法。推荐系统已经成为现代数字服务中不可或缺的一部分,...
《Python期末大作业——采用Neo4j的基于协同过滤电影推荐系统》是一个综合性的项目,旨在教授学生如何利用Python编程语言、大数据处理技术以及Neo4j图数据库来构建一个电影推荐系统。该项目不仅包含了完整的源代码,...
《基于协同过滤算法的音乐推荐系统》是一篇深入探讨协同过滤推荐算法在音乐推荐系统中的应用的毕业论文。本文旨在为计算机科学、数据科学、人工智能等领域的学生和研究人员提供一个全面理解并实施协同过滤算法的框架...
在本实例中,我们将探讨如何使用 PySpark(Python 接口)实现基于 MLlib 的协同过滤推荐算法——交替最小二乘法(Alternating Least Squares, ALS),用于用户和物品的推荐。 协同过滤是推荐系统中最常用的方法之一...
基于协同过滤算法的电影推荐系统设计与实现——整合登录、搜索、浏览与评价功能,使用Python与Django框架与MySQL数据库进行后台管理。,基于协同过滤的Python+Django电影推荐系统——支持多种功能与后台管理模块,以...
基于用户的协同过滤算法:给用户推荐与他兴趣相似的用户喜欢的物品。 协同过滤算法的优点包括: 无需事先对商品或用户进行分类或标注,适用于各种类型的数据。 算法简单易懂,容易实现和部署。 推荐结果准确性较高...
基于用户的协同过滤算法:给用户推荐与他兴趣相似的用户喜欢的物品。 协同过滤算法的优点包括: 无需事先对商品或用户进行分类或标注,适用于各种类型的数据。 算法简单易懂,容易实现和部署。 推荐结果准确性较高...
python毕业设计——基于python和协同过滤算法的电影推荐系统(源码+万字论文+视频演示)+数据库 python毕业设计——基于python和协同过滤算法的电影推荐系统(源码+万字论文+视频演示)+数据库+文档 该项目是个人...
python毕业设计——基于Django和协同过滤算法的电影推荐系统(源码+数据库+说明文档).zip 建立电影数据库: 创建一个电影数据库,其中包含电影的各种信息,如名称、类型、演员、导演等。 实现用户评分功能: 允许...