1ï¼ڑ هٹ¨و€پè؟é€ڑو€§
آ آ هڈ¯ن»¥و£€وµ‹و‰€ç»™çڑ„点ن¸ وک¯هگ¦وœ‰çژ¯çڑ„ï¼ڑ
آ
آ
و¦‚ه؟µï¼ڑ
- ه¹¶وں¥é›†ï¼ڑ(union-find sets)
ن¸€ç§چ简هچ•çڑ„用途ه¹؟و³›çڑ„集هگˆ. ه¹¶وں¥é›†وک¯è‹¥ه¹²ن¸ھن¸چ相ن؛¤é›†هگˆï¼Œèƒ½ه¤ںه®çژ°è¾ƒه؟«çڑ„هگˆه¹¶ه’Œهˆ¤و–ه…ƒç´ و‰€هœ¨é›†هگˆçڑ„و“چن½œï¼Œه؛”用ه¾ˆه¤ڑ,ه¦‚ه…¶و±‚و— هگ‘ه›¾çڑ„è؟é€ڑهˆ†é‡ڈن¸ھو•°ç‰م€‚وœ€ه®Œç¾ژçڑ„ه؛”用ه½“ه±ï¼ڑه®çژ°Kruskarç®—و³•و±‚وœ€ه°ڈç”ںوˆگو ‘م€‚
- ه¹¶وں¥é›†çڑ„精髓(هچ³ه®ƒçڑ„ن¸‰ç§چو“چن½œï¼Œç»“هگˆه®çژ°ن»£ç پو¨،و؟è؟›è،Œçگ†è§£ï¼‰ï¼ڑ
1م€پMake_Set(x) وٹٹو¯ڈن¸€ن¸ھه…ƒç´ هˆه§‹هŒ–ن¸؛ن¸€ن¸ھ集هگˆ
هˆه§‹هŒ–هگژو¯ڈن¸€ن¸ھه…ƒç´ çڑ„父ن؛²èٹ‚点وک¯ه®ƒوœ¬è؛«ï¼Œو¯ڈن¸€ن¸ھه…ƒç´ çڑ„祖ه…ˆèٹ‚点ن¹ںوک¯ه®ƒوœ¬è؛«ï¼ˆن¹ںهڈ¯ن»¥و ¹وچ®وƒ…ه†µè€Œهڈک)م€‚
2م€پFind_Set(x) وں¥و‰¾ن¸€ن¸ھه…ƒç´ و‰€هœ¨çڑ„集هگˆ
وں¥و‰¾ن¸€ن¸ھه…ƒç´ و‰€هœ¨çڑ„集هگˆï¼Œه…¶ç²¾é«“وک¯و‰¾هˆ°è؟™ن¸ھه…ƒç´ و‰€هœ¨é›†هگˆçڑ„祖ه…ˆï¼پè؟™ن¸ھو‰چوک¯ه¹¶وں¥é›†هˆ¤و–ه’Œهگˆه¹¶çڑ„وœ€ç»ˆن¾وچ®م€‚
هˆ¤و–ن¸¤ن¸ھه…ƒç´ وک¯هگ¦ه±ن؛ژهگŒن¸€é›†هگˆï¼Œهڈھè¦پ看ن»–ن»¬و‰€هœ¨é›†هگˆçڑ„祖ه…ˆوک¯هگ¦ç›¸هگŒهچ³هڈ¯م€‚
هگˆه¹¶ن¸¤ن¸ھ集هگˆï¼Œن¹ںوک¯ن½؟ن¸€ن¸ھ集هگˆçڑ„祖ه…ˆوˆگن¸؛هڈ¦ن¸€ن¸ھ集هگˆçڑ„祖ه…ˆï¼Œه…·ن½“è§پç¤؛و„ڈه›¾
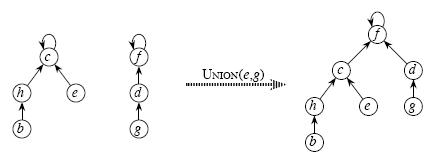
3م€پUnion(x,y) هگˆه¹¶x,yو‰€هœ¨çڑ„ن¸¤ن¸ھ集هگˆ
هگˆه¹¶ن¸¤ن¸ھن¸چ相ن؛¤é›†هگˆو“چن½œه¾ˆç®€هچ•ï¼ڑ
هˆ©ç”¨Find_Setو‰¾هˆ°ه…¶ن¸ن¸¤ن¸ھ集هگˆçڑ„祖ه…ˆï¼Œه°†ن¸€ن¸ھ集هگˆçڑ„祖ه…ˆوŒ‡هگ‘هڈ¦ن¸€ن¸ھ集هگˆçڑ„祖ه…ˆم€‚ه¦‚ه›¾
آ
- ه¹¶وں¥é›†çڑ„ن¼کهŒ–
1م€پFind_Set(x)و—¶ è·¯ه¾„هژ‹ç¼©
ه¯»و‰¾ç¥–ه…ˆو—¶وˆ‘ن»¬ن¸€èˆ¬é‡‡ç”¨é€’ه½’وں¥و‰¾ï¼Œن½†وک¯ه½“ه…ƒç´ ه¾ˆه¤ڑن؛¦وˆ–وک¯و•´و£µو ‘هڈکن¸؛ن¸€و،链و—¶ï¼Œو¯ڈو¬،Find_Set(x)都وک¯O(n)çڑ„ه¤چو‚ه؛¦ï¼Œوœ‰و²،وœ‰هٹو³•ه‡ڈه°ڈè؟™ن¸ھه¤چو‚ه؛¦ه‘¢ï¼ں
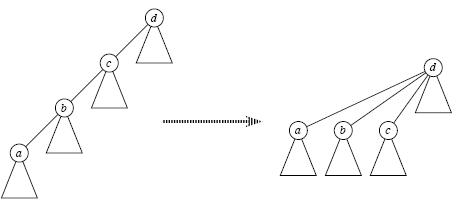
ç”و،ˆوک¯è‚¯ه®ڑçڑ„,è؟™ه°±وک¯è·¯ه¾„هژ‹ç¼©ï¼Œهچ³ه½“وˆ‘ن»¬ç»ڈè؟‡"递وژ¨"و‰¾هˆ°ç¥–ه…ˆèٹ‚点هگژ,"ه›و؛¯"çڑ„و—¶ه€™é،؛ن¾؟ه°†ه®ƒçڑ„هگه™èٹ‚点都直وژ¥وŒ‡هگ‘祖ه…ˆï¼Œè؟™و ·ن»¥هگژه†چو¬،Find_Set(x)و—¶ه¤چو‚ه؛¦ه°±هڈکوˆگO(1)ن؛†ï¼Œه¦‚ن¸‹ه›¾و‰€ç¤؛ï¼›هڈ¯è§پ,路ه¾„هژ‹ç¼©و–¹ن¾؟ن؛†ن»¥هگژçڑ„وں¥و‰¾م€‚
2م€پUnion(x,y)و—¶ وŒ‰ç§©هگˆه¹¶
هچ³هگˆه¹¶çڑ„و—¶ه€™ه°†ه…ƒç´ ه°‘çڑ„集هگˆهگˆه¹¶هˆ°ه…ƒç´ ه¤ڑçڑ„集هگˆن¸ï¼Œè؟™و ·هگˆه¹¶ن¹‹هگژو ‘çڑ„é«که؛¦ن¼ڑ相ه¯¹è¾ƒه°ڈم€‚
آ
آ
آ
package com.algorithm.common.tree;
import com.algorithm.lib.StdOut;
/**
* هٹ¨و€پè؟é€ڑو€§و£€وں¥ (ه¹¶وں¥é›†ç®—و³•)
* @author lijunqing
*/
public class UF {
/**
* ièٹ‚点çڑ„父èٹ‚点(集هگˆ)
*/
private int[] id; // id[i] = parent of i
/**
* i集هگˆن¸هگèٹ‚点و•°é‡ڈ
*/
private int[] sz; // sz[i] = number of objects in subtree rooted at i
/**
* 集هگˆو€»و•°
*/
private int count; // number of components
/**
* هˆه§‹هŒ–Nن¸ھ集هگˆ
*/
public UF(int N) { // nè،¨ç¤؛و‰€وœ‰و•°ه€¼ه°±وک¯count
if(N < 0)
throw new IllegalArgumentException();
count=N;
id=new int[N];
sz=new int[N];
for(int i=0; i < N; i++) {
id[i]=i;
sz[i]=1;
}
}
/**
* وں¥و‰¾ن¸€ن¸ھه…ƒç´ و‰€هœ¨çڑ„集هگˆï¼ˆه…¶ç²¾é«“وک¯و‰¾هˆ°è؟™ن¸ھه…ƒç´ و‰€هœ¨é›†هگˆçڑ„祖ه…ˆï¼‰ ه°±وک¯و‰¾هˆ°و”¹ه…ƒç´ و‰€هœ¨é›†هگˆçڑ„祖ه…ˆ
*/
public int find(int p) {
if(p < 0 || p >= id.length)
throw new IndexOutOfBoundsException();
while(p != id[p]) //// 相ç‰è،¨ç¤؛و‰¾هˆ°ç¥–ه…ˆ
p=id[p];
return p;
}
/**
* è؟”ه›é›†هگˆو€»و•°
*/
public int count() {
return count;
}
/**
* هˆ¤و–pqوک¯هگ¦هœ¨هگŒن¸€é›†هگˆن¸
*/
public boolean connected(int p, int q) {
return find(p) == find(q);
}
/**
* هگˆه¹¶çڑ„و—¶ه€™ه°†ه…ƒç´ ه°‘çڑ„集هگˆهگˆه¹¶هˆ°ه…ƒç´ ه¤ڑçڑ„集هگˆن¸ï¼Œè؟™و ·هگˆه¹¶ن¹‹هگژو ‘çڑ„é«که؛¦ن¼ڑ相ه¯¹è¾ƒه°ڈ
*/
public void union(int p, int q) {
int i=find(p);
int j=find(q);
if(i == j)
return;
// make smaller root point to larger one
if(sz[i] < sz[j]) { // ه…ƒç´ ه°‘çڑ„集هگˆهگˆه¹¶هˆ°ه…ƒç´ ه¤ڑçڑ„集هگˆن¸
id[i]=j; // içڑ„父èٹ‚点وک¯j
sz[j]+=sz[i];
} else {
id[j]=i; // jçڑ„父èٹ‚点وک¯i
sz[i]+=sz[j]; // و”¹هڈک父èٹ‚点çڑ„ه€¼(ه€¼è¶ٹه¤§è،¨ç¤؛ه…¶هگèٹ‚点è¶ٹه¤ڑ)
}
count--;
}
public static void main(String[] args) {
int N=10;
UF uf=new UF(N);
uf.union(1, 2);
uf.union(3, 4);
uf.union(6, 7);
uf.union(2, 7);
int a=uf.find(6);
System.out.println(a);
StdOut.println(uf.count() + " components");
}
}
آ 0 1 1 3 3 5 1 6 8 9آ









相ه…³وژ¨èچگ
ه†…ه®¹و¦‚è¦پï¼ڑوœ¬و–‡è¯¦ç»†ن»‹ç»چن؛†ه¹¶وں¥é›†è؟™ن¸€و ‘ه½¢و•°وچ®ç»“و„هڈٹه…¶هœ¨هٹ¨و€پè؟é€ڑو€§é—®é¢کن¸çڑ„ه؛”用م€‚ن¸»è¦په†…ه®¹هŒ…و‹¬ه¹¶وں¥é›†çڑ„هں؛وœ¬و¦‚ه؟µم€په®çژ°و–¹و³•م€پè·¯ه¾„هژ‹ç¼©ن¸ژوŒ‰ç§©هگˆه¹¶çڑ„ن¼کهŒ–ç–略,ن»¥هڈٹهœ¨ç¤¾ن؛¤ç½‘络ه¥½هڈ‹ه…³ç³»م€پ电路و؟è؟é€ڑو€§و£€وµ‹ه’Œهœ°ه›¾éپ“è·¯è؟é€ڑ...
ه¹¶وں¥é›†وک¯ن¸€ç§چé«کو•ˆçڑ„و•°وچ®ç»“و„,ن¸»è¦پ用ن؛ژه¤„çگ†é›†هگˆçڑ„èپ”é€ڑو€§é—®é¢ک,ه°¤ه…¶هœ¨هˆ¤و–ن¸¤ن¸ھèٹ‚点وک¯هگ¦ه±ن؛ژهگŒن¸€ن¸ھè؟é€ڑهˆ†é‡ڈو—¶è،¨çژ°ه‡؛色م€‚ه®ƒç”±و•°ç»„و„ه»؛,و•°ç»„çڑ„ن¸‹و ‡ه¯¹ه؛”ن؛ژèٹ‚点,و•°ç»„çڑ„ه€¼هˆ™ç”¨و¥è،¨ç¤؛èٹ‚点ن¹‹é—´çڑ„è؟é€ڑه…³ç³»م€‚ن¸‹é¢ه°†è¯¦ç»†è®¨è®؛ه¹¶...
- ه¹¶وں¥é›†ن¸ژو ‘ه‰–م€په—çٹ¶é“¾ç‰وٹ€وœ¯ç»“هگˆï¼Œهڈ¯ن»¥ç”¨ن؛ژ解ه†³و›´ه¤چو‚çڑ„هٹ¨و€پè؟é€ڑو€§é—®é¢کم€‚ 综ن¸ٹو‰€è؟°ï¼Œ"ه¹¶وں¥é›†ه…¥é—¨ه¦ن¹ ه¹¶وں¥é›†"çڑ„资و؛گهڈ¯èƒ½وک¯é’ˆه¯¹هˆه¦è€…çڑ„و•™ç¨‹ï¼Œé€ڑè؟‡â€œه¹¶وں¥é›†.pdfâ€è؟™ن¸ھو–‡و،£ï¼Œن½ ه°†èƒ½ه¤ںو·±ه…¥çگ†è§£ه¹¶وں¥é›†çڑ„هں؛وœ¬و¦‚ه؟µم€پ...
م€ٹ C++ ن؟®ç‚¼ه…¨و™¯وŒ‡هچ—ï¼ڑهچپن؛” م€‹çھپç ´ç®—و³•وپé™گï¼ڑه¹¶وں¥é›†ه¦‚ن½•è½»و¾وگه®ڑوœ€و£کو‰‹çڑ„è؟é€ڑو€§é—®é¢کï¼ںhttps://lenyiin.blog.csdn.net/article/details/142865958?spm=1001.2014.3001.5502 è؟™ç¯‡هچڑه®¢و‰€و¶‰هڈٹçڑ„و‰€وœ‰ه®Œو•´ن»£ç پ م€‚وœ¬ç¯‡...
هœ¨وڈگن¾›çڑ„هژ‹ç¼©هŒ…"ه›¾è®؛- ه›¾çڑ„è؟é€ڑو€§- ه¹¶وں¥é›†هˆ¤و–è؟é€ڑو€§.pdf"ن¸ï¼Œه¾ˆهڈ¯èƒ½وک¯è¯¦ç»†è®²è§£ن؛†ه¦‚ن½•è؟گ用ه¹¶وں¥é›†è؟™ن¸€و•°وچ®ç»“و„و¥è§£ه†³ه›¾çڑ„è؟é€ڑو€§é—®é¢ک,هŒ…و‹¬çگ†è®؛هں؛ç،€م€پç®—و³•ه®çژ°م€په®ن¾‹هˆ†وگç‰م€‚é€ڑè؟‡ه¦ن¹ è؟™ن»½èµ„و–™ï¼Œن½ هڈ¯ن»¥و·±ه…¥çگ†è§£ه¹¶وژŒوڈ،...
هœ¨ه®وˆکه؛”用ن¸ï¼Œه¦‚ç»™ه®ڑçڑ„部هˆ†ن»£ç پو‰€ç¤؛,وˆ‘ن»¬هڈ¯ن»¥çœ‹هˆ°ه¹¶وں¥é›†è¢«ç”¨ن؛ژ解ه†³ه›¾çڑ„è؟é€ڑو€§هˆ¤و–é—®é¢ک,ن»¥هڈٹو›´ه¤چو‚çڑ„و•Œهڈ‹ه…³ç³»هˆ¤و–é—®é¢کم€‚هœ¨ه¤„çگ†ه›¾çڑ„è؟é€ڑو€§و—¶ï¼Œé€ڑè؟‡ن¸چو–و‰§è،Œ`union`و“چن½œè؟وژ¥ç›¸é‚»èٹ‚点,وœ€هگژé€ڑè؟‡`find`و“چن½œو£€وں¥ن»»و„ڈن¸¤...
ه¹¶وں¥é›†وک¯ن¸€ç§چهœ¨ه›¾è®؛ه’Œç®—و³•è®¾è®،ن¸ه¸¸ç”¨çڑ„离و•£و•°ه¦ç»“و„,ن¸»è¦پ用ن؛ژه¤„çگ†ن¸€ن؛›ن¸چ相ن؛¤é›†هگˆçڑ„هگˆه¹¶ن¸ژوں¥è¯¢é—®é¢کم€‚è؟™ن¸ھهژ‹ç¼©هŒ…و–‡ن»¶â€œه›¢ن¼™و•°وچ®â€وک¾ç„¶هŒ…هگ«ن؛†ن¸€ن؛›ن¸ژه¹¶وں¥é›†ç®—و³•ç›¸ه…³çڑ„练ن¹ و•°وچ®ه’Œهڈ¯èƒ½çڑ„é¢ک解,目çڑ„وک¯ه¸®هٹ©ه¦ن¹ 者و›´ه¥½هœ°çگ†è§£...
**ه¹¶وں¥é›†**(Union-Find Set)وک¯ن¸€ç§چو•°وچ®ç»“و„,用ن؛ژه¤„çگ†ن¸€ن؛›ن¸چ相ن؛¤é›†هگˆçڑ„هگˆه¹¶هڈٹوں¥è¯¢é—®é¢ک,é€ڑه¸¸ç”¨و¥è§£ه†³هٹ¨و€پè؟é€ڑو€§é—®é¢کم€‚ه¹¶وں¥é›†و”¯وŒپن¸¤ç§چن¸»è¦پçڑ„و“چن½œï¼ڑ**ه¹¶و“چن½œ**(Union)ه’Œ**وں¥و‰¾و“چن½œ**(Find)م€‚ه¹¶و“چن½œç”¨ن؛ژهگˆه¹¶ن¸¤ن¸ھ...
ه¹¶وں¥é›†ç»ڈه¸¸è¢«ç”¨ن؛ژ需è¦پهٹ¨و€پç»´وٹ¤ن¸€ن؛›ن¸چ相ن؛¤é›†هگˆçڑ„è؟é€ڑو€§é—®é¢کن¸ï¼Œه¦‚社ن؛¤ç½‘络ن¸هˆ¤و–ن¸¤ن¸ھ用وˆ·وک¯هگ¦ه±ن؛ژهگŒن¸€ç¤¾هŒ؛,وˆ–وک¯è®،ç®—وœ؛网络ن¸و£€وµ‹ç½‘络çڑ„è؟é€ڑو€§ç‰م€‚و¤ه¤–,算و³•é—®é¢کن¸çڑ„è·¯ه¾„هژ‹ç¼©وٹ€وœ¯ه’ŒوŒ‰ç§©هگˆه¹¶وٹ€وœ¯وک¯ه¹¶وں¥é›†وڈگé«کو•ˆçژ‡çڑ„...
هœ¨ه®é™…ه؛”用ن¸ï¼Œن¾‹ه¦‚هˆ¤و–网络ن¸çڑ„ن¸¤هڈ°è®،ç®—وœ؛وک¯هگ¦هڈ¯ن»¥ç›´وژ¥é€ڑن؟،م€پ社ن؛¤ç½‘络ن¸çڑ„ن؛؛é™…ه…³ç³»هˆ†وگم€پو— هگ‘ه›¾çڑ„è؟é€ڑو€§و£€وµ‹ç‰هœ؛و™¯ï¼Œéƒ½هڈ¯ن»¥هˆ©ç”¨ه¹¶وں¥é›†و¥è§£ه†³é—®é¢کم€‚ه¹¶وں¥é›†çڑ„é«کو•ˆو€§ه’Œç®€و´پو€§ن½؟ه…¶هœ¨ç®—و³•ç«èµ›ه’Œه®é™…编程ن¸éƒ½ه¾—هˆ°ن؛†ه¹؟و³›...
ه¸¦وƒه¹¶وں¥é›†ï¼ˆWeighted Union-Find)وک¯ن¸€ç§چهœ¨و•°وچ®ç»“و„ن¸ç”¨ن؛ژه¤„çگ†ن¸چ相ن؛¤é›†هگˆï¼ˆDisjoint Set)çڑ„ç®—و³•ï¼Œه®ƒé€ڑè؟‡هگˆه¹¶è؟‡ç¨‹و¥ه‡ڈه°‘集هگˆçڑ„و•°é‡ڈ,هگŒو—¶è€ƒè™‘هگˆه¹¶و“چن½œçڑ„وƒé‡چم€‚ن»¥ن¸‹وک¯ن¸€ن¸ھé’ˆه¯¹ه¸¦وƒه¹¶وں¥é›†و¨،و؟çڑ„资و؛گوڈڈè؟°ï¼ڑ 资و؛گو ‡é¢ک...
ه¹¶وں¥é›†وک¯ن¸€ç§چ用ن؛ژه¤„çگ†é›†هگˆهگˆه¹¶ن¸ژوں¥è¯¢çڑ„وٹ½è±،و•°وچ®ç±»ه‹ï¼Œن¸»è¦په؛”用ن؛ژ解ه†³è؟é€ڑو€§é—®é¢ک,ن¾‹ه¦‚هˆ¤و–ه›¾ن¸çڑ„ن¸¤ن¸ھèٹ‚点وک¯هگ¦هœ¨هگŒن¸€è؟é€ڑهˆ†é‡ڈه†…م€‚هœ¨وœ¬è§£é¢کوٹ¥ه‘ٹن¸ï¼Œوˆ‘ن»¬ه°†وژ¢è®¨ه¹¶وں¥é›†ç®—و³•هœ¨PKU(هŒ—ن؛¬ه¤§ه¦ï¼‰çڑ„ن¸‰éپ“é¢کç›®ï¼ڑPKU1182م€پPKU...
5. **ه؛”用و،ˆن¾‹**ï¼ڑه¹¶وں¥é›†ه¸¸ç”¨ن؛ژ解ه†³ن¸چ相ن؛¤é›†هگˆçڑ„é—®é¢ک,ه¦‚هˆ¤و–ه›¾ن¸وک¯هگ¦هکهœ¨çژ¯م€پ网络è؟é€ڑو€§é—®é¢کم€پ社ن؛¤ç½‘络ن¸çڑ„وœ‹هڈ‹ه…³ç³»وں¥è¯¢ç‰م€‚هœ¨ACMç«èµ›ن¸ï¼Œه¦‚“è؟é€ڑ组ن»¶â€م€پ“وœ€è؟‘ه…¬ه…±ç¥–ه…ˆâ€ç‰é—®é¢کن¸ï¼Œéƒ½èƒ½çœ‹هˆ°ه¹¶وں¥é›†çڑ„è؛«ه½±م€‚ 6. *...
ه¹¶وں¥é›†وک¯ن¸€ç§چ用ن؛ژه¤„çگ†ه…ƒç´ 集هگˆçڑ„هٹ¨و€پو•°وچ®ç»“و„,ه¸¸è¢«ه؛”用ن؛ژه›¾è®؛م€پè®،ç®—وœ؛网络م€پو•°وچ®وŒ–وژکç‰é¢†هںںم€‚ه…¶و ¸ه؟ƒهٹں能وک¯و”¯وŒپن¸¤ç§چو“چن½œï¼ڑهگˆه¹¶ن¸¤ن¸ھ集هگˆï¼ˆه¹¶و“چن½œï¼‰ن¸ژوں¥è¯¢وںگن¸ھه…ƒç´ و‰€ه±çڑ„集هگˆï¼ˆوں¥و“چن½œï¼‰م€‚ه¹¶وں¥é›†هœ¨è§£ه†³ه…·وœ‰é«که؛¦ه…³èپ”و€§çڑ„...
ه¹¶وں¥é›†وک¯ن¸€ç§چهœ¨ه›¾è®؛ه’Œو•°وچ®ç»“و„ن¸ه¹؟و³›ن½؟用çڑ„ç®—و³•ï¼Œن¸»è¦پ用و¥è§£ه†³ç½‘络è؟é€ڑو€§é—®é¢کم€‚هœ¨è؟™ن¸ھ2010ه¹´7وœˆçڑ„وµ™و±ںه¤§ه¦è¯¾ç¨‹è®¾è®،ن¸ï¼Œه¦ç”ںن»¬è¢«è¦پو±‚هˆ©ç”¨ه¹¶وں¥é›†و¥و£€وں¥ç½‘络çڑ„è؟é€ڑçٹ¶و€پم€‚è؟™وک¯ن¸€ن¸ھه…¸ه‹çڑ„离و•£و•°ه¦ه’Œç®—و³•ه؛”用çڑ„ه®è·µن»»هٹ،,...
ه¹¶وں¥é›†ï¼ˆUnion-Find Sets)وک¯و•°وچ®ç»“و„ن¸ن¸€ç§چ用ن؛ژç®،çگ†ه…ƒç´ 集هگˆçڑ„é«کو•ˆç®—و³•ï¼Œه®ƒن¸»è¦په¤„çگ†ن¸¤ن¸ھو“چن½œï¼ڑè؟وژ¥ï¼ˆunion)ن¸ژوں¥و‰¾ï¼ˆfind)م€‚هœ¨ه¹¶وں¥é›†ن¸ï¼Œه…ƒç´ 被هˆ†هˆ°ن¸چهگŒçڑ„集هگˆن¸ï¼Œو¯ڈن¸ھ集هگˆن»£è،¨ن¸€ن¸ھ独立çڑ„组ن»¶م€‚è؟وژ¥و“چن½œه°†ن¸¤ن¸ھه…ƒç´ ...
1. poj2524.cppï¼ڑè؟™وک¯ن¸€ن¸ھPOJ(Problem Setter's Online Judge)çڑ„编程é¢ک目,é€ڑه¸¸و¶‰هڈٹهˆ°ç‰¹ه®ڑçڑ„ç®—و³•é—®é¢ک,هڈ¯èƒ½éœ€è¦پهˆ©ç”¨ه¹¶وں¥é›†è§£ه†³è؟é€ڑو€§وˆ–è·¯ه¾„وں¥و‰¾é—®é¢کم€‚ 2. hdoj1233وœ€ه°ڈç”ںوˆگو ‘,ه…‹é²پو–¯هچ،ه°”.cppï¼ڑوœ€ه°ڈç”ںوˆگو ‘وک¯ه›¾è®؛...
ه¹¶وں¥é›†ن¸»è¦په؛”用ن؛ژه¤„çگ†هٹ¨و€پè؟é€ڑو€§é—®é¢ک,ن¾‹ه¦‚هˆ¤و–ن¸¤ن¸ھه…ƒç´ وک¯هگ¦ه±ن؛ژهگŒن¸€ن¸ھ集هگˆï¼Œن»¥هڈٹه°†ن¸چه±ن؛ژهگŒن¸€ن¸ھ集هگˆçڑ„ه…ƒç´ è؟›è،Œهگˆه¹¶م€‚ #### ن؛Œم€پç‰ن»·ç±»هڈٹه…¶و€§è´¨ هœ¨è®¨è®؛ه¹¶وں¥é›†ن¹‹ه‰چ,وˆ‘ن»¬ه…ˆن؛†è§£ç‰ن»·ç±»çڑ„相ه…³و¦‚ه؟µم€‚ 1. **ç‰ن»·ç±»**ï¼ڑ...
ه¹¶وں¥é›†وک¯ن¸€ç§چهœ¨هˆ†و•£çڑ„و•°وچ®... ه¹¶وں¥é›†وک¯ن¸€ç§چه®ç”¨çڑ„و•°وچ®ç»“و„,é€ڑè؟‡é«کو•ˆهœ°ه¤„çگ†é›†هگˆçڑ„هگˆه¹¶ه’Œوں¥è¯¢ï¼Œه¹؟و³›ه؛”用ن؛ژهگ„ç§چ需è¦په¤„çگ†è؟é€ڑو€§é—®é¢کçڑ„هœ؛و™¯م€‚ç†ں练وژŒوڈ،ه¹¶وں¥é›†çڑ„هژںçگ†ه’Œه®çژ°ï¼Œه¯¹ن؛ژ解ه†³ç®—و³•ç«èµ›ه’Œه®é™…ه·¥ç¨‹é—®é¢ک都ه…·وœ‰é‡چè¦پو„ڈن¹‰م€‚
هœ¨ه®é™…ه؛”用ن¸ï¼Œه¦‚网络è؟وژ¥م€پ社ن؛¤ç½‘络هˆ†وگم€په›¾çڑ„è؟é€ڑو€§هˆ¤و–ç‰هœ؛و™¯ï¼Œن¼کهŒ–هگژçڑ„ه¹¶وں¥é›†èƒ½ه¤ںوڈگن¾›é«کو•ˆçڑ„解ه†³و–¹و،ˆم€‚وµ‹è¯•ç”¨ن¾‹هڈ¯ن»¥è®¾è®،وˆگن¸€ç³»هˆ—çڑ„ `Union` ه’Œ `Find` 请و±‚,éھŒè¯په¹¶وں¥é›†çڑ„و£ç،®و€§ه’Œو€§èƒ½م€‚ é€ڑè؟‡çگ†è§£ه’Œç†ں练وژŒوڈ،...