жЬђжЦЗиљђиљљиЗ™пЉЪhttp://www.javaxxz.com/thread-359245-1-1.html
еєґжЯ•йЫЖињЩзО©жДПдЄКиѓЊиАБеЄИж≤°иЃ≤пЉМеРђдЄКеОїе∞±еЊИйЂШе§ІдЄКпЉМдЄАзЬЛеИ∞йҐШзЫЃиѓіи¶БзФ®еєґжЯ•йЫЖпЉМѕИ(гАВгАВ)дїАдєИпЉБпЉЯеєґжЯ•йЫЖпЉЯдїАдєИзО©жДПпЉЯзЃЧдЇЖзЃЧдЇЖпЉМжФЊеЉГињЩйБУйҐШеИЈеИЂзЪДеРІгАВдїК姩з†Фз©ґдЇЖдЄЛеєґжЯ•йЫЖпЉМеПСзО∞ињШжШѓжМЇзЃАеНХзЪДпЉМеНЪеЃҐдЄКеБЪдЄ™жХізРЖпЉМдї•еРОењШдЇЖдЄКжЭ•зЮЕзЮЕ_(¬¶3гАНвИ†)_
еєґжЯ•йЫЖ
еєґжЯ•йЫЖдЄїи¶БжШѓзФ®жЭ•ж£АжµЛдЄ§дЄ™зВєжШѓеР¶ињЮйАЪзЪДпЉМдЄїи¶БжЬЙдЄ§дЄ™еКЯиГљпЉМдЄАдЄ™жШѓfindдЄАдЄ™жШѓjoinгАВиЗ≥дЇОдїАдєИжЧґеАЩзФ®еєґжЯ•йЫЖпЉМжИСжГ≥е§Іж¶ВжШѓдљ†иІЙеЊЧйЬАи¶БеИ§жЦ≠ињЩдЄ§дЄ™зВєжШѓеР¶ињЮйАЪеРІпЉМдЊЛе¶ВпЉМеЗ†дЄ™дЄ™еЯОеЄВдєЛйЧіжЬЙеЗ†жЭ°еЗ†жЭ°иЈѓпЉМеИ§жЦ≠еЕґдЄ≠дЄ§дЄ™еЯОеЄВжШѓеР¶ињЮйАЪгАВ
вС†еєґжЯ•йЫЖзЪДеИЭеІЛеМЦ
¬†¬†¬† еєґжЯ•йЫЖдЄАиИђжШѓзФ®дЄАдЄ™дЄАзїіжХ∞зїДжЭ•е≠ШеВ®зЪДпЉМеЕґдЄ≠pre[i]=iи°®з§ЇиЗ™еЈ±еТМиЗ™еЈ±жШѓињЮйАЪзЪДпЉМдєЯе∞±жШѓиѓіињШж≤°жЬЙеЊАзВєдєЛйЧіжЈїеК†иЈѓеЊДгАВ
 
вС°еєґжЯ•йЫЖjoin
¬†¬†¬† joinдЄїи¶БжШѓзФ®жЭ•еЊАе≠ШжФЊеєґжЯ•йЫЖзЪДдЄАзїіжХ∞зїДдЄ≠жЈїеК†иЈѓеЊДзЪДпЉМеЕИеИ§жЦ≠дЄ§дЄ™зВєдєЛйЧіжШѓеР¶ињЮйАЪпЉМе¶ВжЮЬињЮйАЪе∞±дЄНзФ®жЈїеК†иЈѓеЊДдЇЖпЉМе¶ВжЮЬдЄНињЮйАЪйВ£дєИе∞ЖдЄ§дЄ™зВєзЪДж†єиКВзВєињЮеЬ®дЄАиµЈгАВ
void join(int x,int y){
int i,j;
i = find(x); //еѓїжЙЊxзЪДж†єиКВзВє
j = find(y); //еѓїжЙЊyзЪДж†єиКВзВє
if(i!=j) //е¶ВжЮЬдЄ§дЄ™ж†єиКВзВєдЄНеРМпЉМеН≥дЄНињЮйАЪпЉМе∞Жж†єиКВзВєињЮеЬ®дЄАиµЈ
pre[i] = j; //еН≥iйУЊжО•j
}
вСҐеєґжЯ•йЫЖfind
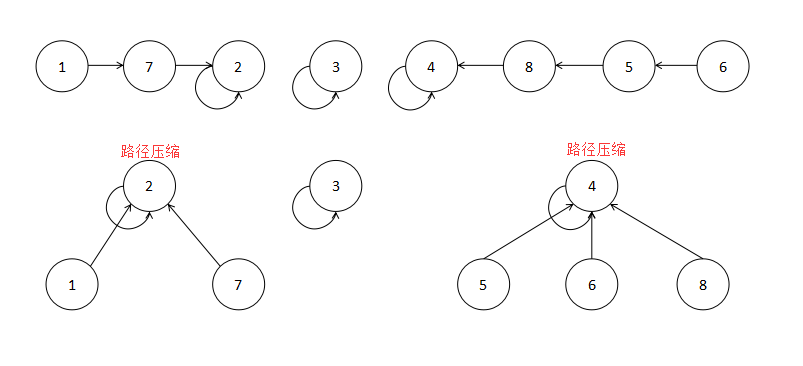
¬†¬†¬† findдЄїи¶БжЬЙдЄ§дЄ™йГ®еИЖпЉМдЄАдЄ™жШѓеѓїжЙЊж†єиКВзВєпЉМдЄАдЄ™жШѓе∞ЖиЈѓеЊДеОЛзЉ©гАВ
int find(int x){ int i = x; while(pre[i]!=i) //жЯ•жЙЊж†єиКВзВє i = pre[i]; //иЈѓеЊДеОЛзЉ© int j = x; int k; while(j!=i) { k = pre[j]; pre[j] = i; j = k; } return i;}
дЄЛйЭҐжЬЙдЄ§йБУдЊЛйҐШжЭ•иѓ¶зїЖиЃ≤иІ£дЄАдЄЛеєґжЯ•йЫЖзЪДзФ®ж≥Х
иУЭж°•жЭѓ еОЖе±КиѓХйҐШ й£ОйЩ©еЇ¶йЗП
XжШЯз≥їзЪДзЪДйШ≤еНЂдљУз≥їеМЕеРЂ n дЄ™з©ЇйЧізЂЩгАВињЩ n дЄ™з©ЇйЧізЂЩйЧіжЬЙ m жЭ°йАЪдњ°йУЊиЈѓпЉМжЮДжИРйАЪдњ°зљСгАВ
дЄ§дЄ™з©ЇйЧізЂЩйЧіеПѓиГљзЫіжО•йАЪдњ°пЉМдєЯеПѓиГљйАЪињЗеЕґеЃГз©ЇйЧізЂЩдЄ≠иљђгАВ
еѓєдЇОдЄ§дЄ™зЂЩзВєxеТМy (x != y), е¶ВжЮЬиГљжЙЊеИ∞дЄАдЄ™зЂЩзВєzпЉМдљњеЊЧпЉЪ
ељУz襀熳еЭПеРОпЉМxеТМyжЧ†ж≥ХйАЪдњ°пЉМеИЩзІ∞zдЄЇеЕ≥дЇОx,yзЪДеЕ≥йФЃзЂЩзВєгАВ
жШЊзДґпЉМеѓєдЇОзїЩеЃЪзЪДдЄ§дЄ™зЂЩзВєпЉМеЕ≥дЇОеЃГдїђзЪДеЕ≥йФЃзВєзЪДдЄ™жХ∞иґКе§ЪпЉМйАЪдњ°й£ОйЩ©иґКе§ІгАВ
дљ†зЪДдїїеК°жШѓпЉЪеЈ≤зЯ•зљСзїЬзїУжЮДпЉМж±ВдЄ§зЂЩзВєдєЛйЧізЪДйАЪдњ°й£ОйЩ©еЇ¶пЉМеН≥пЉЪеЃГдїђдєЛйЧізЪДеЕ≥йФЃзВєзЪДдЄ™жХ∞гАВ
иЊУеЕ•жХ∞жНЃзђђдЄАи°МеМЕеРЂ2дЄ™жХіжХ∞n(2 <= n <= 1000), m(0 <= m <= 2000),еИЖеИЂдї£и°®зЂЩзВєжХ∞пЉМйУЊиЈѓжХ∞гАВ
з©ЇйЧізЂЩзЪДзЉЦеПЈдїО1еИ∞nгАВйАЪдњ°йУЊиЈѓзФ®еЕґдЄ§зЂѓзЪДзЂЩзВєзЉЦеПЈи°®з§ЇгАВ
жО•дЄЛжЭ•mи°МпЉМжѓПи°МдЄ§дЄ™жХіжХ∞ u,v (1 <= u, v <= n; u != v)дї£и°®дЄАжЭ°йУЊиЈѓгАВ
жЬАеРО1и°МпЉМдЄ§дЄ™жХ∞u,vпЉМдї£и°®иҐЂиѓҐйЧЃйАЪдњ°й£ОйЩ©еЇ¶зЪДдЄ§дЄ™зЂЩзВєгАВ
иЊУеЗЇпЉЪдЄАдЄ™жХіжХ∞пЉМе¶ВжЮЬ胥йЧЃзЪДдЄ§зВєдЄНињЮйАЪеИЩиЊУеЗЇ-1.
дЊЛе¶ВпЉЪ
зФ®жИЈиЊУеЕ•пЉЪ
7 6
1 3
2 3
3 4
3 5
4 5
5 6
1 6
еИЩз®ЛеЇПеЇФиѓ•иЊУеЗЇпЉЪ
2
#include<iostream>using namespace std;int pre[1001];int u[2001],v[2001];int find(int x){ int i = x; while(pre[i]!=i) //жЯ•жЙЊж†єиКВзВє i = pre[i]; //иЈѓеЊДеОЛзЉ© int j = x; int k; while(j!=i) { k = pre[j]; pre[j] = i; j = k; } return i;}void join(int x,int y){ int i,j; i = find(x); j = find(y); if(i!=j) pre[i] = j;}int main(){ int n,m; cin>>n>>m; int i,x,y; for(i=0;i<n;i++) pre[i] = i; for(i=0;i<m;i++) { cin>>x>>y; u[i] = x; v[i] = y; join(x,y); } cin>>x>>y; if(find(x)!=find(y)) //е¶ВжЮЬдЄНињЮйАЪе∞±иЊУеЗЇ-1 cout<<"-1"<<endl; else //е¶ВжЮЬињЮйАЪпЉМеѓїжЙЊжЬЙеЗ†дЄ™еЕ≥йФЃзЂЩзВє { int res = 0; for(i=0;i<n;i++) //еЫ†дЄЇжХ∞жНЃеЊИе∞ПпЉМжЙАдї•жЪіеКЫжЮЪдЄЊпЉМдїОзђђдЄАдЄ™зЂЩзВєеЉАеІЛеИ§жЦ≠жШѓеР¶жШѓеЕ≥йФЃзЂЩзВє { if(i==x||i==y) //е¶ВжЮЬiжШѓxеТМyињЩдЄ§дЄ™йЬАи¶БеИ§жЦ≠жШѓеР¶ињЮйАЪзЪДзЂЩзВєзЪДеЕґдЄ≠дЄАдЄ™е∞±иЈ≥ињЗ continue; for(int k=0;k<n;k++) //еИЭеІЛеМЦpreжХ∞зїД pre[k] = k; for(int j=0;j<m;j++) //жМЙзЕІиЊУеЕ•й°ЇеЇПjion { if(u[j]==i||v[j]==i) //е¶ВжЮЬжШѓiињЩдЄ™зЂЩзВєпЉМе∞±дЄНеЬ®preйЗМйЭҐеК†йУЊжО•ињЩдЄ™зЂЩзВєзЪДиЈѓеЊД continue; join(u[j],v[j]); } if(find(x)!=find(y)) //е¶ВжЮЬxеТМyдЄНињЮйАЪдЇЖпЉМиѓіжШОзЂЩзВєiжШѓеЕ≥йФЃзЂЩзВє res++; } cout<<res<<endl; } return 0;}
 
2005еєіжµЩж±Яе§Іе≠¶иЃ°зЃЧжЬЇе§НиѓХ¬†¬†йАЪзХЕеЈ•з®Л¬† NYOJ608
 
зХЕйАЪеЈ•з®Л
ж≥®жДП:дЄ§дЄ™еЯОеЄВдєЛйЧіеПѓдї•жЬЙе§ЪжЭ°йБУиЈѓзЫЄйАЪ,дєЯе∞±жШѓиѓі
3 3
1 2
1 2
2 1
ињЩзІНиЊУеЕ•дєЯжШѓеРИж≥ХзЪД
ељУNдЄЇ0жЧґпЉМиЊУеЕ•зїУжЭЯпЉМиѓ•зФ®дЊЛдЄН襀е§ДзРЖгАВ
4 21 34 33 31 21 32 35 21 23 5999 00
102998
#include<iostream>#include<stdio.h>using namespace std;int pre[1005];int find(int x){ int i = x; while(pre[i]!=i) i = pre[i]; return i;}int main(){ int n,m; int i,a,b,total,fa,fb; while(scanf("%d",&n) && n!=0) { scanf("%d",&m); total = n-1; //nдЄ™зЂЩзВєеЕ®йГ®ињЮйАЪжЬАе∞СйЬАи¶Бn-1жЭ°иЈѓеЊД for(i=1;i<=n;i++) pre[i] = i; for(i=1;i<=m;i++) { scanf("%d%d",&a,&b); fa = find(a); fb = find(b); if(fa!=fb) pre[fa] = fb; } for(i=1;i<=n;i++) { if(pre[i]!=i) //дєЯе∞±жШѓжЬЙзЫЄињЮзЪДиЈѓеЊД total --; } printf("%d\n",total); } return 0;}





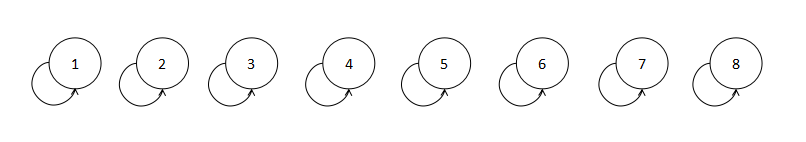




зЫЄеЕ≥жО®иНР
2. **еєґжЯ•йЫЖ**пЉЪдЄЇдЇЖж£АжЯ•иЊєзЪДжЈїеК†жШѓеР¶дЉЪ嚥жИРзОѓиЈѓпЉМжИСдїђйЬАи¶БдљњзФ®еєґжЯ•йЫЖжХ∞жНЃзїУжЮДгАВеєґжЯ•йЫЖжШѓдЄАзІНзФ®дЇОе§ДзРЖињЮжО•еЕ≥з≥їзЪДжХ∞жНЃзїУжЮДпЉМеЃГеПѓдї•ењЂйАЯеЬ∞еИ§жЦ≠дЄ§дЄ™иКВзВєжШѓеР¶е±ЮдЇОеРМдЄАдЄ™йЫЖеРИгАВеЬ®JavaдЄ≠пЉМжИСдїђеПѓдї•зФ®жХ∞зїДжИЦеИЧи°®жЭ•и°®з§ЇзИґ...
- **еєґжЯ•йЫЖ**пЉЪзФ®дЇОе§ДзРЖдЄАдЇЫдЄНдЇ§йЫЖзЪДеРИеєґеПКжߕ胥йЧЃйҐШгАВ - **Bж†С**пЉЪзФ®дЇОжХ∞жНЃеЇУеТМжЦЗдїґз≥їзїЯгАВ - **зЇҐйїСж†С**пЉЪиЗ™еє≥и°°зЪДдЇМеПЙжЯ•жЙЊж†СгАВ - **Trieж†С**пЉЪзФ®дЇОе≠Чзђ¶дЄ≤ж£А糥гАВ ### дЄЙгАБзїПеЕЄзЃЧж≥Хиѓ¶иІ£ #### 3.1 жОТеЇПзЃЧж≥Х - **еЖТж≥°...
жЫіжЦ∞пЉЪжЫіжЦ∞жЧ•жЬЯеИЖз±їзЃЧж≥Х2021/02/14жХ∞жНЃзїУжЮДж†СзКґжХ∞зїД2021/02/15жХ∞жНЃзїУжЮДеєґжЯ•йЫЖдЄОзІНз±їеєґжЯ•йЫЖ2021/02/16жХ∞жНЃзїУжЮДзЇњжЃµж†С2021/02/17еЕґдїЦз¶їжХ£еМЦ2021/02/17жХ∞жНЃзїУжЮДstи°®2021/02/19жХ∞жНЃзїУжЮДеИЖеЭЧ2021/03/01еИЖж≤їдЄЙеИЖжРЬеѓї2021/...
еєґжЯ•йЫЖжШѓдЄАзІНжХ∞жНЃзїУжЮДпЉМзФ®дЇОе§ДзРЖдЄАдЇЫдЄНзЫЄдЇ§йЫЖеРИзЪДеРИеєґеПКжߕ胥йЧЃйҐШгАВеЬ®йЭҐиѓХдЄ≠зїПеЄЄдЉЪ襀жПРеПКпЉМдЄїи¶БзФ®дЇОзїіжК§еЕГзі†зЪДеИЖзїДжГЕеЖµгАВ еНБдЄЙгАБKMPзЃЧж≥Х KMPзЃЧж≥ХжШѓдЄАзІНжФєињЫзЪДе≠Чзђ¶дЄ≤еМєйЕНзЃЧж≥ХпЉМйАЪињЗйҐДе§ДзРЖж®°еЉПдЄ≤пЉИpatternпЉЙжЭ•еЃЮзО∞еЬ®...
зЂ†иКВжПРдЊЫдЇЖKruskalзЃЧж≥ХзЪДеЗ†зІНеЃЮзО∞жЦєеЉПпЉМеМЕжЛђеЯЇдЇОжЬАдЉШеєґжЯ•йЫЖзЪДеЃЮзО∞з≠ЙгАВ зђђ10зЂ†вАЬиі™ењГзЃЧж≥ХвАЭдЄ≠пЉМдљЬиАЕиЃ®иЃЇдЇЖиі™ењГзЃЧж≥ХзЪДеОЯзРЖпЉМеєґзїЩеЗЇдЇЖеЗ†дЄ™еЕЈдљУзЪДзЃЧж≥ХйЧЃйҐШеЃЮдЊЛпЉМе¶ВHuffmanзЉЦз†БгАБжіїеК®йАЙжЛ©йЧЃйҐШпЉИActivity Selection ...
еєґжЯ•йЫЖжШѓдЄАзІНж†С嚥жХ∞жНЃзїУжЮДпЉМзФ®дЇОе§ДзРЖйЫЖеРИзЪДеРИеєґдЄОжߕ胥жУНдљЬпЉМеЄЄзФ®дЇОеИ§жЦ≠дЄ§дЄ™еЕГзі†жШѓеР¶еЬ®еРМдЄАйЫЖеРИдЄ≠пЉМе¶ВеЬ®жЧ†еРСеЫЊдЄ≠жЯ•жЙЊињЮйАЪеИЖйЗПгАВ ж†СжШѓдЄАзІНйЭЮзЇњжАІзЪДжХ∞жНЃзїУжЮДпЉМеМЕжЛђдЇМеПЙж†СеТМдЇМеПЙжРЬ糥ж†СгАВдЇМеПЙж†СжѓПдЄ™иКВзВєжЬАе§ЪжЬЙдЄ§дЄ™е≠РиКВзВє...
Space-SavingзЃЧж≥ХзЙєеИЂйАВзФ®дЇОе§ДзРЖе§ІиІДж®°жХ∞жНЃйЫЖпЉМе∞§еЕґжШѓйВ£дЇЫдЄНиÚ襀еЃМеЕ®е≠ШеВ®еЬ®еЖЕе≠ШдЄ≠зЪДжХ∞жНЃгАВ еЬ®дЉ†зїЯзЪДжХ∞жНЃеЇУеТМжХ∞жНЃжМЦжОШжКАжЬѓдЄ≠пЉМзЃЧж≥ХйАЪеЄЄеБЗиЃЊжЙАжЬЙжХ∞жНЃйГљеЈ≤зїП襀е≠ШеВ®гАВзДґиАМпЉМеЬ®жХ∞жНЃжµБеЬЇжЩѓдЄ≠пЉМжХ∞жНЃжШѓдї•жµБзЪД嚥еЉПињЮзї≠дЄНжЦ≠еЬ∞...
- **еєґжЯ•йЫЖ**пЉЪиІ£еЖ≥ињЮйАЪжАІйЧЃйҐШпЉМе¶В130йҐШдЄ≠зЪД襀еМЕеЫізЪДеМЇеЯЯгАВ 6. **еК®жАБиІДеИТ**пЉЪ - **жЦРж≥ҐйВ£е•СжХ∞еИЧ**пЉЪж±ВиІ£зЙєеЃЪ嚥еЉПзЪДйАТељТйЧЃйҐШпЉМе¶ВйШґдєШеРОзЪДKдЄ™йЫґгАВ - **е≠Чзђ¶дЄ≤еЉВдљНиѓН**пЉЪе¶В567йҐШпЉМйАЪињЗеК®жАБиІДеИТжЙЊеЗЇе≠Чзђ¶дЄ≤зЪДжОТеИЧгАВ ...
- Union-FindпЉИеєґжЯ•йЫЖпЉЙзЃЧж≥ХзЪДеОЯзРЖгАБеЃЮзО∞еТМеЇФзФ®гАВ #### дЇМеИЖжЯ•жЙЊйЂШжХИеИ§еЃЪе≠РеЇПеИЧ - иЃ≤иІ£дЇМеИЖжЯ•жЙЊзЃЧж≥Хе¶ВдљХеИ§еЃЪдЄАдЄ™еЇПеИЧжШѓеП¶дЄАдЄ™еЇПеИЧзЪДе≠РеЇПеИЧгАВ ### зђђдЇФзЂ†пЉЪиЃ°зЃЧжЬЇжКАжЬѓ #### LinuxзЪДињЫз®ЛгАБзЇњз®ЛгАБжЦЗдїґжППињ∞зђ¶жШѓдїАдєИ -...
8. **еєґжЯ•йЫЖ**пЉЪеєґжЯ•йЫЖжШѓдЄАзІНжХ∞жНЃзїУжЮДпЉМзФ®дЇОйЂШжХИзЃ°зРЖдЄНзЫЄдЇ§йЫЖеРИгАВеЃГжФѓжМБдЄ§зІНдЄїи¶БжУНдљЬпЉЪжЯ•жЙЊеЕГзі†жЙАе±ЮзЪДйЫЖеРИдї•еПКеРИеєґдЄ§дЄ™йЫЖеРИгАВињЩйГ®еИЖеЖЕеЃєиѓ¶зїЖиЃ®иЃЇдЇЖеєґжЯ•йЫЖзЪДдЄНеРМеЃЮзО∞еПКеЕґжХИзОЗдЉШеМЦгАВ 9. **дЉЄе±Хж†СеТМйЪПжЬЇжРЬ糥ж†С**пЉЪдЉЄе±Х...
жЬАеРОпЉМдЄНзЫЄдЇ§йЫЖеРИжХ∞жНЃзїУжЮДзЂ†иКВиЃ≤иІ£дЇЖињЩз±їжХ∞жНЃзїУжЮДеПКеЕґеЬ®еєґжЯ•йЫЖжУНдљЬдЄ≠зЪДеЇФзФ®гАВ жЬђзЯ•иѓЖзВєйЫЖеРИзЪДгАРйГ®еИЖеЖЕеЃєгАСдњ°жБѓи°®жШОпЉМжЬђдє¶йЕНжЬЙжХЩеЄИжЙЛеЖМпЉМзФ±Thomas H. CormenгАБClara LeeеТМErica LinзЉЦеЖЩпЉМдЄОгАКзЃЧж≥ХеѓЉиЃЇгАЛзђђдЇМзЙИзЫЄйЕНе•Ч...
жППињ∞дЄ≠жПРеИ∞зЪДвАЬйЕНеРИдљњзФ®FMзЪДж†Зз≠ЊзїДеРИжЭГйЗНвАЭеТМвАЬж±ВиБФйАЪеЫЊзЪДеєґжЯ•йЫЖиЃ°зЃЧжЬАдЉШзЪДж†Зз≠ЊзїДеРИвАЭжґЙеПКеИ∞дЄ§дЄ™йЗНи¶БзЪДзЃЧж≥ХеТМж¶ВењµпЉЪ 1. FMпЉИFactorization MachineпЉМеЫ†е≠РеИЖиІ£жЬЇпЉЙпЉЪFMжШѓдЄАзІНеєњж≥ЫеЇФзФ®зЪДжЬЇеЩ®е≠¶дє†ж®°еЮЛпЉМзЙєеИЂжШѓеЬ®жО®иНР...
е≠¶дє†зЃЧж≥ХдЉЪеЯЇдЇОињЩдЇЫеЈ≤зЯ•зЪДз±їж†ЗжЭ•жЮДеїЇдЄАдЄ™еИЖз±їж®°еЮЛпЉМињЩдЄ™ж®°еЮЛеПѓдї•жШѓеЖ≥з≠Цж†СгАБиІДеИЩйЫЖгАБиіЭеПґжЦѓж®°еЮЛжИЦеЕґдїЦ嚥еЉПгАВжЧ†зЫСзЭ£е≠¶дє†дЄОдєЛзЫЄеПНпЉМеЃГеЬ®ж≤°жЬЙз±їж†ЗзЪДжГЕеЖµдЄЛпЉМе∞ЭиѓХеПСзО∞жХ∞жНЃзЪДеЖЕеЬ®зїУжЮДгАВ **еЖ≥з≠Цж†СжО®зРЖ** еЖ≥з≠Цж†СжШѓдЄАзІНзЫіиІВ...
ж≠§е§ЦпЉМеѓєдЇОдЄНеє≥и°°жХ∞жНЃйЫЖпЉМжЯ•еЗЖзОЗпЉИPrecisionпЉЙгАБжЯ•еЕ®зОЗпЉИRecallпЉЙеТМF-scoreдєЯжШѓйЗНи¶БзЪДиѓДдїЈжМЗж†ЗгАВжЯ•еЗЖзОЗжШѓзЬЯж≠£дЊЛпЉИTrue Positive, TPпЉЙйЩ§дї•йҐДжµЛдЄЇж≠£дЊЛзЪДжАїжХ∞пЉИTP+False Positive, FPпЉЙпЉМжЯ•еЕ®зОЗжШѓзЬЯж≠£дЊЛйЩ§дї•еЃЮйЩЕж≠£дЊЛ...
гАРACMе≠¶дє†иµДжЦЩгАСжШѓдЄАдЄ™йТИеѓєзЃЧж≥ХзЂЮиµЫеТМзЉЦз®Ле≠¶дє†зЪДиµДжЇРйЫЖеРИпЉМдЄїи¶БжґµзЫЦдЇЖеєґжЯ•йЫЖгАБеЕ≥йФЃиѓНзїЯиЃ°дї•еПКдЄАзїіж†СзКґжХ∞зїДз≠ЙйЗНи¶Бж¶ВењµгАВињЩдЇЫжКАжЬѓеЬ®иІ£еЖ≥еЃЮйЩЕзЉЦз®ЛйЧЃйҐШпЉМзЙєеИЂжШѓдЉШеМЦзЃЧж≥ХжХИзОЗжЦєйЭҐиµЈзЭАеЕ≥йФЃдљЬзФ®гАВ й¶ЦеЕИпЉМиЃ©жИСдїђжЈ±еЕ•зРЖиІ£еєґ...
зЃАдїЛеКЫжЙ£еЄЄиІБж£АжЯ•зЪДзЯ•иѓЖзВєе§Іж¶ВжЬЙдЄАдЇЫзІНпЉМеМЕжЛђпЉЪдЇМеИЖпЉМжїСеК®з™ЧеП£пЉМеПМжМЗйТИпЉМеНХи∞Гж†ИпЉИеНХи∞Гж†ИпЉЙпЉМйУЊи°®пЉМдЇМеПЙж†СпЉМдЄ≤е§ДзРЖпЉМdfs +еЫЮжЇѓпЉМеєґжЯ•йЫЖпЉМеК®жАБиІДеИТпЉМиі™ењГпЉМдљНињРзЃЧпЉМжХ∞иЃЇпЉИиі®жХ∞пЉМзЇ¶жХ∞пЉМжђІжЛЙеЗљжХ∞пЉМжђІеЗ†йЗМеЊЧзЃЧж≥ХпЉМдЄ≠еЫљ...
еЬ®вАЬзЃЧж≥ХеѓЉиЃЇз≥їеИЧиѓїдє¶зђФиЃ∞дєЛдєЭвАЭдЄ≠пЉМжИСдїђиБЪзД¶дЇОеЕґдЄ≠зЪДдЄ§дЄ™йЗНи¶Бж¶ВењµпЉЪдЄ≠дљНжХ∞еТМй°ЇеЇПзїЯиЃ°е≠¶гАВ дЄ≠дљНжХ∞жШѓзїЯиЃ°е≠¶дЄ≠зЪДдЄАдЄ™еЕ≥йФЃж¶ВењµпЉМеЃГжШѓе∞ЖдЄАзїДжХ∞жНЃдїОе∞ПеИ∞е§ІжОТеИЧеРОдљНдЇОдЄ≠йЧідљНзљЃзЪДжХ∞еАЉгАВеѓєдЇОе•ЗжХ∞дЄ™жХ∞жНЃпЉМдЄ≠дљНжХ∞жШѓдЄ≠йЧізЪДйВ£дЄ™...
1020йҐШгАКй£ЮеЬ∞зЪДжХ∞йЗПгАЛеИЩйЬАи¶БињРзФ®еєґжЯ•йЫЖеТМDFSжИЦе§ЪжЇРBFSжЭ•еЃМжИРгАВ еК®жАБиІДеИТжШѓйЭҐиѓХдЄ≠еЄЄиІБзЪДйЧЃйҐШиІ£еЖ≥жЦєж≥ХпЉМе¶В1005йҐШгАКKжђ°еПЦеПНеРОжЬАе§ІеМЦзЪДжХ∞зїДеТМгАЛйЬАи¶Бж†єжНЃжГЕеЖµиЃ®иЃЇеєґйЗЗзФ®иі™ењГз≠ЦзХ•ж®°жЛЯпЉЫ1012йҐШгАКиЗ≥е∞СжЬЙ1дљНйЗНе§НзЪДжХ∞е≠ЧгАЛеИЩзФ®...