上节里的最速下降算法有个最明显的特征就是迭代,迭代所带来的特征便是经常反复应用矩阵A。在线性代数里面,矩阵的特征向量的特征便是在矩阵乘法运算的时候不改变方向(除了反向)。
我们用符号B 来代表这个不断被应用的矩阵。
一个矩阵的特征向量不是唯一的,因为可以任意缩放它们,但是对应的特征值却是不变的唯一的。好像看不出来与上一篇的联系哈,但是线性代数的一大特征就是任意向量可以看作是线性无关向量的组合 。
当反复的应用B在特征向量上时,如果特征值|v| < 1,那么特征向量就意味着缩短,反之就是延长 。当一个特征向量不断收缩的时候,就可以意味着收敛,哪怕另外的向量是向外延展的。想想向量加法就知道了。
记得上一节里求梯度的时候,对于正定对称A,得到f'(x) = Ax - b么,通过Ax = b这个式子,我们想着往x成为一个特征向量上靠,最好是能从这个式子里弄出个x迭代的关系,迭代的关系里还有矩阵与x的反复应用。我们可以通过这样变形,
(D + E)x = b,这里D只拥有A的对角元素,E拥有其它元素。再进一步的变形
Dx = -Ex + b => (这样做是因为对角阵很好求逆)
x = -D''Ex + D''b => (''再次用来表示求逆)
x = Bx + z =>(B和z只是记号)
x(i+1) = Bx(i) + z
(这样就满足要求了,x再变成特征向量线性组合的形式, 很好很强大)想法是好,但是有一点不得不说明,就是B经常不是对称的,甚至在确定性上也保证不了(就算A是对称的),这就决定了此方法好归好,但不一定收敛 哦。
详细的就不讲了,特征向量在线性代数里真的用处太多了,可惜就是上学那会儿不知道有这么多神奇。
上面是引子, 下边才是本篇的重点。
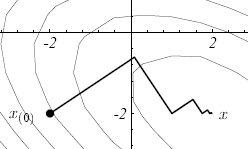 最速下降有一个问题,就是迭代总在几个早期的的方向上进行 ,左边的图上就可见一斑。
最速下降有一个问题,就是迭代总在几个早期的的方向上进行 ,左边的图上就可见一斑。
如此变产生这样一个想法,要是我们能够在 那几个正交方向上每次只 进行一步 ,一步完成那方向上应该移动的贴近解x的距离,那该有多好(直接由x【最优点】往那些方向上引垂线)。想法是绝妙,但是是空想,要是你知道了x,那问题不就直接解决了是吧。所以问题需要变通,转换成A正交。所谓A正交,是指d(i)'Ad(j) = 0,就称向量d(i)和d(j)是A正交的,也就是共轭。
我们利用共轭其实是利用这样一个特点,A * x 这种形式可以看作是对x进行线性变换(变形 ),x'Ax对应的形式正是椭圆(椭球)。我们讲x'Ax=0,如果A是单位对角矩阵,那么x'与x是正交的。说到底,d(i)'与d(j)是共轭的,正是因为他们在未变形的空间是正交的 。我们也是利用这样一个特点,来达到每次方向上只走一次,且一次便是该方向上的最优点。我盘算了一下,如果简单上一张图在这里也会显得比较突兀,文档里的图太大,还要缩小画布,mspaint又做不了此事,还是免了。
在此之前,可能要插上一点内容,当我们在最速下降过程中应用特征向量时,定义能量模(energe norm)||e||(A) = (e'Ae)1/2.这里的1/2是开平方的意思。我们用特征向量来表示e(i),详细的也不列了,贴图不方便,这里面又表示式子很困难。 最小化这个模和最小化f(x)是等价的。因为f(x+e) = f(x) + 1/2 * e'Ae. (x+p)是函数上任意一点。看待这个能量模的时候同样可以用空间变形的角度,能量模相等的同心圆在变形后成为同心椭圆线 ,这些都是函数映射的等值线。A正交的向量正是未变形空间切线与半径的关系。
到此,我们的需求 也就变成了e(i+1)和d(i)是A正交 ,这样的变化同样可达到一个方向只走一次的特性。因为切线点已经是距离圆心最近的点了。这样的话,需求就变成了找到这些共轭方向 。我们有一个计算共轭方向的Gram-Schmidt Conjugation方法,原理和Gram-Schmidt正交化如出一辙,是 利用投影原理 在已有共轭基的基础上构造一个新的共轭基。但这种方法有个重大的问题是需要保存所有计算过的共轭方向在内存中以用来计算新的共轭方向。这个劣势使得它基本获得不了青睐,直到共轭方向展现除了一些让人轻松的特性。
详细讲很痛苦,必不可少列出些代数式式子变化和一些trick,其实最根本,自认为最有益的东西已经在上面讲出来了,再讲下去只是生成共轭梯度方向上的一些让人欣慰的变化,就此打住。
共轭梯度下降法在神经网络中加快训练速度有些帮助,假设误差曲面是二次型的。
分享到:









相关推荐
共轭梯度法(Conjugate Gradient Method)是一种在数值分析和优化领域中广泛使用的算法,主要用于求解大型对称正定线性方程组。它由Richard H. Byrd、Daniel W. Forsythe、Maurice G. Golub及John H. Wilkinson等人...
引入了二次形式的概念并用于推导最速下降、共轭方向和共轭梯度的方法。 特征向量被解释并用于检查雅可比方法、最速下降和共轭梯度的收敛性。 其他主题包括预处理和非线性共轭梯度方法。 我已竭尽全力使本文易于阅读...
共轭梯度法则在保持简单性的同时,提供了更快的二次收敛性,但并不直接适用于BP网络,需要通过Fletcher-Reeves共轭梯度法进行修改。拟牛顿法是另一种替代方案,它可能比共轭梯度法收敛更快,但对优化过程的精度要求...
共轭梯度法是一种迭代优化算法,用于求解线性方程组,它在目标跟踪的分类网络训练中起到关键作用。 ATOM算法在四个主要的跟踪数据集上达到了新的高度。这些数据集包括GOT-10K、LaSOT、TrackingNet和VOT2018等。GOT-...
2. 梯度下降法 梯度下降法是一种常用的优化算法,课程笔记中对梯度下降法进行了详细的讲解,包括了梯度下降法的定义、搜索方向、步长选择等方面的内容。此外,课程笔记还提供了梯度下降法的实现代码,帮助学生更好...
- **梯度下降法**:介绍了一种基本的优化算法及其变体。 - **最速下降法**:讨论了几种不同的下降方向。 - **算法的选择**:根据问题的特点推荐了不同的算法。 - **拉格朗日法与增广拉格朗日法**:对比了两种常用的...
在高级优化方法中,如共轭梯度法、BFGS和L-BFGS算法,都是梯度下降法的变体,它们被设计来加速收敛过程,并且在许多情况下可以找到全局最小值,尤其是在代价函数具有凸性质的情况下。 总结起来,文件内容涉及了...
- `traincgb`:共轭梯度反向传播,带鲍威尔重启动。 - `trainlm`:Levenberg-Marquardt反向传播。 - `trainrp`:RPROP反向传播。 5. 绘图功能: - `plotfit`:绘制拟合情况。 - `plotresponse`:绘制动态网络的时间...
### PRML读书会笔记知识点概览 #### 一、引言 《Pattern Recognition and Machine Learning》(PRML)是一本经典的机器学习教材,由Christopher M. Bishop撰写。本书以其全面性和深度著称,在机器学习领域内被视为...
在训练神经网络时,工具箱提供了一系列的训练函数,包括梯度下降(`traingd`)、共轭梯度法(`traincg*`)、Levenberg-Marquardt算法(`trainlm`)以及RPROP(`trainrp`)等。这些算法的选择取决于问题的性质和数据的复杂性...
此外,还有更高效的算法,如拟牛顿法和共轭梯度法,它们在保持全局收敛性的前提下,通过更精确地近似海森矩阵(Hessian矩阵)来加速收敛。 在机器学习中,凸优化的应用广泛。例如,逻辑回归、支持向量机、线性回归...
优化算法:共轭梯度,BFGS,L-BFGS 多类别分类:一对多分类 过度拟合:减少特征空间; 正则化。 正则化和正则化线性/逻辑回归,梯度下降 第4周:神经网络:表示形式 非线性假设 动机,代表 前向传播算法 学习功
**求解方法**:同样可以通过梯度下降法或更高效的算法如牛顿法、共轭梯度法等来最小化损失函数。 **多分类问题**:对于多于两类的问题,可以使用“一对多”策略(one-vs-all)来进行多分类。 #### 二、模型评估与...
- **共轭梯度法**:在某些情况下比梯度下降法更快的一种算法。 - **二阶条件**:用于判断局部极小点或极大点的充分条件。 - **凸函数**:凸函数的性质对于确定全局最优解非常重要。 - **海森矩阵**:在多元函数中...
这一章节集中讨论了梯度下降法、牛顿法、拟牛顿法(包括BFGS和L-BFGS)以及共轭梯度法等。这些方法主要利用目标函数的一阶或二阶导数信息,迭代逼近最优解。无论是在理论研究还是在实际应用中,这些方法都扮演着极其...
对于线性规划问题,笔记提到了拉格朗日乘数法、梯度下降法等优化算法,以及如何将约束问题转化为无约束问题,如罚函数法(外点罚函数和内点罚函数)和障碍函数法。 最后,笔记还提及了遗传算法中的变异运算,这是...
- **优化算法**:优化算法如梯度下降法、共轭梯度法等在图像处理中用于求解最优解。 #### 4. 实验与应用案例 - 书中可能包含了一些具体的实验案例,展示如何运用上述数学方法解决实际问题。 ### 四、教育意义 该...
1. **数值线性代数**:矩阵运算、线性方程组的求解方法(如高斯消元法、LU分解、QR分解、SVD分解等),以及迭代法(如雅可比法、高斯-塞德尔法、共轭梯度法等)。 2. **插值与拟合**:拉格朗日插值、牛顿插值、样条...
3. **常见凸优化算法**:如梯度下降法、拟牛顿法、共轭梯度法、梯度投影法等,这些算法在解决实际问题时各有优缺点,会根据问题的特性选择合适的方法。 4. **线性规划与凸优化**:线性规划是最简单的凸优化问题类型...
- **共轭梯度法**(CG):一种高效的迭代求解线性方程组的方法。 - **确定性反褶积**(EDD):一种用于预测和外推地震数据的技术。 #### 十、广义线性和非线性反演 - **广义反演**:一种处理非线性反演问题的方法...