任意一个拥有n个变量的boolean function可以被一个r(r<n)阶的PTG来实现。具体细节现在不看,不然又扯出来一大堆东西。PTG来解决问题看成是多个LTG的组合,只不过输入被扩展了。
在典型的boolean function的时候,当变量数又比较小,可以用K-map来进行简单有效的分析,挖出可行的LTG组合形式。
Function Counting Theorem:位于general position的m个点能被线性二分的情况的数目
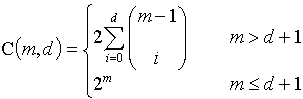
我们以Points in General Position的概念出发,来对这个问题来进行说明。
在一个d维空间的m个点中,如果不存在d+1个点同处在d-1维的超平面 上,那么我们认为这m个点处在General Position上,此时m>d。例如三点不共线。
如果m<d, 那么就变成没有m-2维的超平面包含这m个点,意义不大,且又没法感受,因为超过了三维空间就没法用立体图形表示了。说到底,回到线性代数的表示方式:也就是(m>n时)。
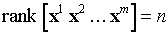
general position在定理证明里是充要条件,当然它也有表述问题时其优秀的特性,例如m个随机点位于Gerneral position的概率是接近1的:)
现在我们来证明一下这个定理:
设m点集X={x1, x2, ..xm}实数域d维空间,记C(m, d)为完成{X+,X-}分离出来的线性二分的数目,X+表明在分隔超平面正侧。其实我们这里讨论的是没有标记过的点,就如非监督学习一样,只是考察能不能把它们分开,是能够完成可分的任务的所有可行情况的数目。
考虑一个新点,xm+1, 记x‘ = {x1, x2, ..xm,xm+1},这m+1个点同样要满足general position的条件,那么可以存在一些通过xm+1的超平面可以完成对X的划分,记这种划分的数目为D。对于D中的每一种情况,将会有两个新的划分出现,{X+, X- U {Xm+1}}和{X+ U {Xm+1}, X-}。
这是因为对于处于general position的情况下,D中的那个分隔超平面可以移动无限小的距离而不影响到分隔的结果{X+, X-}。因此对于D中每个旧的分隔情况,会增加出一个新的来 :C(m+1, d)=C(m, d) - D + 2D = C(m, d) + D.
然而D=C(m, d-1),因为限制了超平面必须通过一点 ,其实就使得问题等价于d-1维度的问题 。C(m+1, d) = C(m, d) + C(m, d-1)。
这样的迭代关系 ,我们可以解得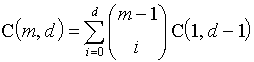
C(1, n) = 2,因为一个点只可能有两种划分情况,既而更加简化,在m<d+1时,更加简单:
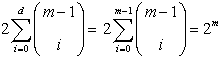
一个单独n-input LTG可以完成对处于general position上的m个点划分的概率是:
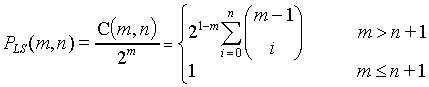
当n->无穷的时候,这个概率的极限是1,限制条件是m<2(n+1) 。LTG不能处理m>3(n+1)的问题,但有这问题的时候我们还可以提高维度。
General Position其实是这个问题的上界,因为在任意点集合,出现不同的线性二分的情况叫少了,数目少了,概率自然就降下来了。
对于属于布尔空间的m个点,能被一个r阶PTG进行二分的概率是多少呢
Function counting的数目上界是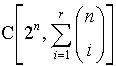 。这里右边的是多项式的自由度,看到最上面写的那个定理么,funciton counting theorem里看得出方程也是随m递增的,2的n次方做为左边的极限带来的就是最大值。
。这里右边的是多项式的自由度,看到最上面写的那个定理么,funciton counting theorem里看得出方程也是随m递增的,2的n次方做为左边的极限带来的就是最大值。
再往下的就不说了。
其实写了这么多更多只是对于Cover theorem的一个佐证 :The probability that classes are linearly separable increases when the features are nonlinearly mapped to a higher dimensional feature space.
低维空间不可分转换到高维空间有可能线性可分 。
分享到:






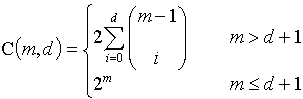
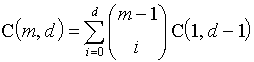
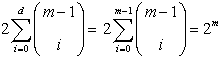
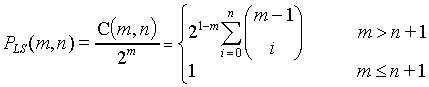
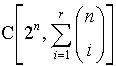 。这里右边的是多项式的自由度,看到最上面写的那个定理么,funciton counting theorem里看得出方程也是随m递增的,2的n次方做为左边的极限带来的就是最大值。
。这里右边的是多项式的自由度,看到最上面写的那个定理么,funciton counting theorem里看得出方程也是随m递增的,2的n次方做为左边的极限带来的就是最大值。


相关推荐
统计学习方法主要涉及模式识别、概率论和统计推断等基础知识。这些方法包括监督学习、无监督学习和半监督学习。书中重点讨论了线性回归、逻辑回归、支持向量机、决策树、随机森林、神经网络、贝叶斯网络等多种模型...
### CCIE笔记——详细命令介绍 #### 一、基本配置命令 在Cisco设备上进行配置时,有许多基本的命令是必须掌握的。这些命令对于设备的初始设置、安全管理以及日常维护至关重要。 - **hostname**: 用于更改路由器的...
2. "作业_chapter4_解答(1).pdf":这部分内容可能是第四章的作业解答,可能包含了与特征工程、概率模型或统计学习理论相关的题目,通过解答可以深化对这些章节的理解。 3. "作业_chapter3_解答(1).pdf":同理,这是...
- **序列模式**:在数据分析中,序列模式是指在时间序列数据中发现的重复模式或趋势。 - **时间序列**:R语言提供了处理时间序列数据的工具,如`ts()`函数,用于创建时间序列对象。 2. **数据保存和输出格式**: ...
贝叶斯决策方法是统计模式识别中的一个基本方法,用这个方法进行分类时要求:各类别总体的概率分布是已知的;要决策分类的类别数是一定的。在连续情况下,假设对要识别的物理对象有 d 种特征观察量 x1, x2, ⋯, xd,...
机器学习手写笔记的作者是为了深化对机器学习课程内容的理解,尤其是对于支持向量机(SVM)等复杂算法的原理,这份笔记不仅用于个人复习,也可能供他人参考。 支持向量机(Support Vector Machine,简称SVM)是一种...
它基于数据,通过模式识别、统计分析和优化算法,使计算机能够从已有的例子中学习,而不是通过人为编程进行特定任务。机器学习可以分为监督学习、无监督学习、半监督学习和强化学习四大类。 监督学习是最常见的机器...
这个过程涉及模式识别、统计推断和优化算法,旨在让计算机从经验中自我提升。 吴恩达的机器学习课程通常涵盖以下几个核心概念: 1. 监督学习:这是最常见的机器学习类型,包括回归和分类问题。例如,线性回归用于...
解决多分类问题的一个常见方法是利用多个弱分类器通过集成学习(ensemble learning)的方式构建出一个强大的分类器。常用的多分类算法包括决策树、随机森林(random forest)等。 ##### 层次聚类 **层次聚类**...
1. 统计学习理论基础:统计学习方法基于概率论和统计学,它包括监督学习、无监督学习和半监督学习等多种模式。书中首先介绍了学习问题的基本框架,包括实例、特征和假设空间。 2. 感知机:感知机是最早提出的二分类...
以上就是Linux系统中一些常用命令的学习笔记。每个命令后面通常可以跟上不同的选项和参数,来满足不同的需求。掌握这些命令,对于Linux系统的日常运维工作至关重要。随着时间的推移,建议持续学习和实践,不断提高对...
监督学习侧重于通过有标签的训练数据来指导模型学习,预测或分类是其最常见的任务。无监督学习则致力于从无标签数据中发现隐藏的结构或模式,聚类和降维是常见的应用场景。这些学习范式的理解和应用是成为一名优秀AI...
这种学习过程通常涉及到统计方法的应用,以从大量数据中提取有用的信息,并基于这些信息做出预测或决策。 机器学习的应用十分广泛,包括但不限于自动驾驶汽车、语音识别、搜索引擎优化、基因组学分析等领域。随着...
在统计学习理论部分,书中讨论了风险最小化、泛化能力和Vapnik-Chervonenkis(VC)维度等概念,这些理论工具帮助我们理解模型复杂度与泛化能力之间的关系,以及如何通过交叉验证选择最佳模型。 习题解答部分是学习...
10. **文本生成**:包括文章摘要、诗歌创作、故事生成等,深度学习模型可以学习语言模式并自动生成连贯的文本。 通过阅读《斯坦福CS224n_自然语言处理与深度学习_笔记_hankcs.pdf》,你可以深入理解这些主题,掌握...
2. 机器学习的分类 - 监督学习(Supervised Learning):这是一种机器学习方式,其中算法通过示例的输入输出对进行训练。监督学习的例子包括分类和回归问题。 - 非监督学习(Unsupervised Learning):在此类学习中...
这本书可能会详细讨论特征提取、分类器设计以及模式识别的统计理论,对于想要深入理解模式识别的同学来说,是一本不可或缺的参考书。 在学习过程中,掌握这些知识点不仅能帮助你建立坚实的理论基础,还能提升解决...
3. 主要课程内容:课程内容涵盖了机器学习、数据挖掘和统计模式识别的广泛主题,包括监督学习、无监督学习、机器学习最佳实践等。监督学习部分涵盖参数/非参数算法、支持向量机、核函数、神经网络;无监督学习部分...
本课程总共需要10周时间,分为18节课,涵盖了机器学习、数据挖掘、统计模式识别等广泛的主题。课程中将使用大量的案例研究,并提供包括视频、PPT课件在内的丰富学习资源。作者黄海广作为中国海洋大学2014级博士生,...