ÕàêÕåÖõ©Çõ║øÕà│õ║Äþ║┐µÇºõ╗úµò░þÜäõ©£ÞÑ┐Õɺ´╝îõ║║Úò┐Õñºõ║åÞ«░µÇºÞÂèµØÑÞÂèÕÀ«õ║å´╝îÕøáõ©║ÕÉîõ©ÇµùÂÚù┤ÚçîÞäæÞóïÚçîÚØóÞúàþÜäõ©£ÞÑ┐Õñ¬ÕñÜõ║å´╝îÕÑ│µ£ïÕÅïµèèµêæþÜäõ©Çõ║øõ╣ªÕìûõ║å´╝îµ£ëþé╣ÕÅ»µâ£´╝îÕŬÞâ¢þø╝µ£øõ╗ÑÕÉÄþö¿õ©ìþØÇÒÇé
 
Õ£¿þ║┐µÇºõ╗úµò░þÜäõ╣ªµ£¼Úçî´╝îÞíîÕêùÕ╝ÅÞ┐ÖÕØùµÿ»Õ¥êµ£ëþö¿þÜä´╝îµ£ÇÕêصÿ»õ©║Þºúµû╣þ¿ïÕÅæÕ▒òÞÁÀµØÑ´╝îþö¿µØÑþí«Õ«Üþ║┐µÇºµû╣þ¿ïþ╗äÞºúþÜäõ©¬µò░´╝îõ╗ÑÕÅèÕ¢óÕ╝Å´╝îÕ¥êÕñÜõ©£ÞÑ┐õ¢áõ╗ѵû╣þ¿ïþÜäÞºÆÕ║ªµØÑþ£ïÕ░▒ÕÑ¢þÉåÞºúþÜäÕñÜÒÇéõ¢åµÿ»õ╣ªµ£¼õ©èÕ£¿µÄ¿õ╗ïÞíîÕêùÕ╝Åõ╗Ä2Úÿ´╝î3ÚÿÂÕê░NÚÿÂþÜäµùÂÕÇÖµêæÞºëÕ¥ùþ║»þ▓╣µÿ»õ©║õ║åÕ║öþö¿ÞÇîÕ║öþö¿´╝îõ╗ÑÕÉĵØÑõ║║þÜäþ£╝ÕàëÕÄ╗þ£ïÞ┐Öõ©¬µÄ¿Õ╣┐þÜäÕç║þÄ░´╝îÕ¥êÕñÜþ╗åÞèéÚâ¢Õ┐¢þòÑÒÇéµâ│µâ│Õàêõ║║Õ£¿õ¢£Õç║Õ╝ÇÕêøµÇºþáöþ®ÂþÜäµùÂÕÇÖµÇØÞÇâÕÅèÚ¬îÞ»üÚù«ÚóÿþÜäµÇØÞÀ»µÿ»µ£ÇÚçìÞªüþÜä´╝îõ©öիܵÿ»õ©ÑÞ░¿þÜä´╝îµë¥Õ»╗þÜäÞ┐çþ¿ïõ©¡õ¢áþ£ïÕê░ÕÄåÕÅ▓ÕÅæÕ▒òþÜäÞ┐çþ¿ïõ©¡Õ¥êÕñÜõ©£ÞÑ┐Õ╣Âõ©ìµÿ»Õªéõ╣ªµ£¼þ╗äþ╗çÕÉÄÕæêþÄ░þ╗Öµêæõ╗¼þÜäÚí║Õ║Åõ©ÇµáÀ´╝îÕ¥¬þØÇÚéúÞ¢¿Þ┐╣õ╝ܵø┤ÕèáÕó×Õèáõ¢áþÜäÕø░µâæÒÇé
 
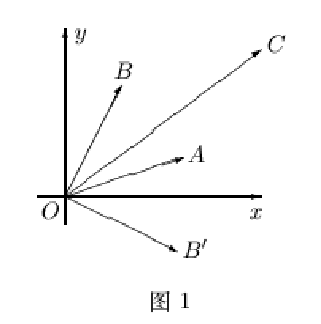
Õ╝òÕàÑÞíîÕêùÕ╝ÅþÜäÞ«░ÕÅÀµÿ»õ©║õ║åµû╣õ¥┐þÜäÞí¿þñ║ÕÆîÞ«íþ«ùµû╣þ¿ïþÜäþ╗äþÜäÞºúÒÇé
a1 x + b1 y=c1┬á┬á┬á┬á µêûÞ«░µêÉÕÉæÚçÅÕ¢óÕ╝Å┬á x [a1] + y [b1] = [c1]┬á┬á┬á┬á┬á ┬á ┬á ┬á õ©ñÞ¥╣Úâ¢õ©ÄOB'ÕüÜÕåàþº»´╝î ┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á
a2 x + b2 y=c2                                      [a2]       [b2]    [c2]            OA*OB' = [a1] * [b2] = a1b2 - a2b1
                                                                                                                            [a2]   [-b1]
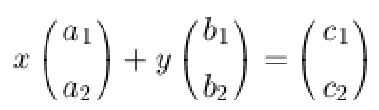 ┬á┬á
┬á┬á 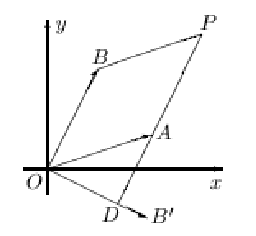
 
S = a1b2 - a2b1 = OA * OB' = |OA||OB|cos<AOB' = |OA||OB|cos(<AOB - TT/2) = |OA||OB|sin<AOB = Õ╣│ÞíîÕøøÞ¥╣Õ¢óµ£ëÕÉæÚØóþº»
 
µêûõ║îÚÿµø┤þ«ÇÕìòþÜä޻ش╝îõ╗úµò░µÂêÕàâµ│ò´╝î x = (c1b2 - c2b1) / (a1b2 - a2b1), y = (a1c2 - a1c1) / (a1b2 - a2b1)
 
Þ┐ÖµùÂÕ╝òÕàÑÞ«░ÕÅÀ[a1 b1] = a1b2 - a2b1, Þ┐ÖÚçîµÿ»õ║îÚÿÂõ╣âÞç│nÚÿÂÞíîÕêùÕ╝ÅþÜäþ¼¼õ©ÇµÄ¿Õè¿Õèø´╝îÞÖ¢þäµÿ¥ÞÇîµÿôÞºü ÒÇé
                         [a2 b2]
õ©ëÚÿÂÞíîÕêùÕ╝Åõ╣ªõ©èÕû£µ¼óõ©Çþ¼öÕ©ªÞ┐ç´╝îµÂêÕàâ´╝îÕ░▒Õ¥ùÕê░õ║å´╝îÕô¬µÿ»Úéúõ╣êÞ¢╗µÿôÕø×õ║ïÒÇéÚù«Úóÿþáöþ®ÂÕÅ»õ╗Ñõ╗Äþë╣õ¥ïÕàѵëï´╝îõ¢åÚÇܵǺþÜäÞ«║Þ»üÚÜÅõ╣ïÞÇîµØÑÒÇé
 
a11x+a12y+a13z=m1
a21x+a22y+a23z=m2
a31x+a32y+a33z=m3
 
µêæõ╗¼þÜäþø«þÜäµÿ»µÂêÕàâÒÇé a12X+a22Y+a32Z=0┬á (Þ«░µÂêÕàâÞ┐çþ¿ïõ©¡õ©èõ©ëÕ╝ÅÚ£ÇÞªüþÜäõ╣ÿµò░,õ¥ïÕªéµêæõ╗¼þÄ░Õ£¿ÞªüÞºúx)
                                     a13X+a23Y+a33Z=0
┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á┬á ┬á ┬á┬á┬á a11X+a21Y+a31Z=ÞºúxµëÇÕ»╣Õ║öþÜäÕêåµ»ì(õ©ëÚÿÂÞíîÕêùÕ╝ÅþÜäÕÇ╝?)
 
õ©ñõ©¬µû╣þ¿ïÞºúõ©ëõ©¬ÕÅÿÚçÅ´╝ƒµêæõ╗¼þÄ░Õ£¿Ú£ÇÞªüÞºúX´╝îY´╝îZÕç║µØÑÒÇéÞ┐ÖÚçîõ¢áÕÅ»õ╗Ñþ£ïÕç║µØÑÞíîÕêùÕ╝ÅաɵîëÞíî(Õêù)Õ▒òÕ╝ÇþÜäÞÁÀÕøá(Õ▒òÕ╝ǵ»önÚÿÂÞíîÕêùÕ╝ŵù®Õç║þÄ░)ÒÇé
õ╗ÄÞºúµû╣þ¿ïþÜäÞºÆÕ║ªµØÑþ£ï´╝îXÕ┐àµÿ»a23,a23,a32,a33þÜäþ║┐µÇºþ╗äÕÉê´╝îÞ«®µêæõ╗¼Õø×Þ┐çÕñ┤þ£ïþ£ïõ║îÚÿÂÞíîÕêùÕ╝Å´╝îÕÅ»õ╗ÑÞ«ñõ©║a1´╝îa2õ╣ÿõ╗ÑþÜäÚ⢵ÿ»õ©ÇÚÿÂÞíîÕêùÕ╝ÅþÜäÕÇ╝´╝îÚéúõ╣êa2Þ┐ÿÚ£ÇÞªüõ╣ÿõ╗Ñ-1´╝îÞïÑÕÉîµáÀõ╗ÑÕÅîõ©ïµáçµØÑÞí¿þñ║þÜä޻ش╝îÚéúõ╣êõ©Äõ©ïµáçÕÆîþÜäÕÑçÕüµ£ëÕà│ÒÇéÚéúõ╣êµêæõ╗¼ÕÅ»õ╗ÑÕ░ØÞ»òÚÇÆÕ¢ÆþÜäµÇØÞÇâ´╝îõ©ìþäµÇÄõ╣êµÄ¿Õ╣┐Õæó´╝îÕæÁÕæÁ´╝îÕªéµ×£Xµÿ» (-1)*(-1) [a22 a23]þÜäÕÇ╝´╝îÚéúõ╣êÕÉîþÉåÕ║öþö¿Õê░Y,Z,ÕÅæþÄ░µ×£þäÂÕÅ»õ╗ÑÒÇéÞ┐ÖµáÀþÜä޻ش╝îÕøø
                                           [a32 a33]
ÚÿÂÞíîÕêùÕ╝Åõ╣ƒµ£ëõ║åÚÇÆÕ¢ÆÕ«Üõ╣ëþÜäµØѵ║É´╝îµêûÞ«©Þ┐Öµÿ»õ╣ªµ£¼õ©èNÚÿÂÞíîÕêùÕ╝ÅþÜäÕÅæþÄ░µÄ¿Õ»╝þ║┐ÞÀ»ÕɺÒÇé
 
ÕàÂÕ«×õ©║õ╗Çõ╣êXþ«ÇÕìòþÜäµÿ»õ║îÚÿÂÞíîÕêùÕ╝ÅþÜäÕÇ╝Õæó´╝îÕ¢ôµêæõ╗¼õ╗ÑÕÉæÚçÅþÜäÕ¢óÕ╝ŵØÑþ£ïÕ¥àÕêØÕºïþÜäõ©ëÕàâµû╣þ¿ïµù´╝îÞïÑõ╗ÑÕÉæÚçÅÕ¢óÕ╝ÅÞí¿þñ║´╝îõ¥ïÕªé
xA + yB + zC = r
Õ¢ôþ¡ëÕ╝Åõ©ñÞ¥╣ÕÉîµùÂõ╣ÿõ╗ÑBXCµù´╝îÕ░▒ÕÅÿµêÉxA*(BXC) = r *(BXC),Þ┐Öõ¥┐µÿ»µêæõ╗¼µëǵâ│ÞªüþÜäþ╗ôµ×£ÒÇé(BXC) = [a2 b3 ÔêÆ a3 b2 , a3 b1 ÔêÆ a1 b3 , a1 b2 ÔêÆ a2 b1] . õ╗ÄÕÉæÚçÅÞ┐Éþ«ùþÜäÕêåÚàìþÄçÞ«íþ«ùÞÇîµØÑÒÇé
 
õ©║õ╗Çõ╣êBXCþÜäÕÇ╝Õªéõ©èµëÇþñ║´╝îBXCÕøáõ©║Õ«âµÿ»õ©Çõ©¬ÕÉæÚçÅ´╝îÕ»╣Õ║öõ║Äþ¼øÕìíÕ░öÕØɵáçþ│╗þÜä޻ش╝îõ╗ÑÕØɵáçþÜäÕ¢óÕ╝ÅÞí¿þñ║þø©Õ¢ôõ¥┐Õê®´╝îõ©ìþö¿ÞÇâÞÖæõ╗╗õ¢òÞºÆÕ║ªþÜäÚù«Úóÿ´╝îÞí¿þñ║µêÉÞ┐Öõ©¬Õ¢óÕ╝ŵ¡úÕÑ¢µÿ»µêæõ╗¼µëÇÚ£ÇÞªüþÜäX´╝îY´╝îZþÜäÕÇ╝´╝îõ©öÕ»╣Õ║öþÜäµÿ»õ║îÚÿÂÞíîÕêùÕ╝ÅþÜäÕÇ╝´╝î´╝Ü´╝ëÒÇé
 
-----------------------------------
Note´╝Ü
Õ£¿µ¼ºÕçáÚçîÕ¥Àþ®║Úù┤Úçî´╝îÕèáµ│òÕ»╣Õ║öÕ╣│þº╗´╝îõ╣ÿµ│òþö¿µØÑÕ«Üõ╣ëµùïÞ¢¼´╝îÚéúõ╣êÕÉæÚçÅþº»Þ┐ÖþºìÕ¢óÕ╝ÅÕàÂÕ«×µë¥õ©ìÕê░ÕÉêþÉåþÜäÞºúÚçè´╝îµ£ëõ║║Þ»┤þÜäÕÑ¢´╝îµò░Õ¡ªµÿ»µ£ëÞÂúþÜä´╝îõ¢åõ╣ƒµÿ»þø▓þø«þÜä´╝îõ©ÇÕêçþÜäõ©ÇÕêçÕç║þÄ░Úâ¢õ©ìµÿ»µùáþø«þÜäþÜäÒÇéÕÉæÚçÅþº»þÜäÕ╝òÕàÑõ╗Äþë®þÉåõ©¡þÜäÕèøþƒ®ÞÇîµØÑ´╝îÕèøþƒ®þÜäµû╣ÕÉæÕ«Üõ╣ëÕÅêµÿ»õ╗ÄÞºÆÚǃÕ║ªµû╣ÕÉæþÜäÕ«Üõ╣ëÞÇîµØÑ´╝îÕøáõ©║ÞºÆÚǃÕ║ªÕŬµ£ëõ©ñõ©¬µû╣ÕÉæ´╝îÚí║µùÂÚÆê´╝îÚÇåµùÂÚÆê´╝îõ©öÕèøþƒ®µÿ»µ£ëÕà│þë®õ¢ôÞ¢¼Õè¿þÜäõ©Çõ©¬ÚçÅ´╝îÕÅêµÿ»ÕÉæÚçÅ´╝îµëÇõ╗ÑÕ«Üõ╣ëµû╣ÕÉæõ©║Õ×éþø┤õ║ÄÕèøõ©ÄÕèøÞçéþí«Õ«ÜþÜäÕ╣│ÚØóÒÇé
 
þ║┐µÇºþ£ƒµÿ»õ©Çõ©¬þë╣ÕÑ¢þÜäµÇºÞ┤¿ÒÇé
Õêåõ║½Õê░´╝Ü







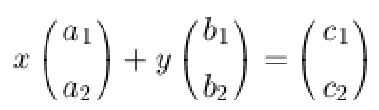 ┬á┬á
┬á┬á 



þø©Õà│µÄ¿ÞìÉ
Þ┐æÕ╣┤µØÑ´╝îÚÜÅþØǵò░µì«ÚçÅþÜäþêåÕÅæÕ╝ÅÕó×Úò┐ÕÆîÞ«íþ«ùÞâ¢ÕèøþÜäµÿ¥ÞæùµÅÉÕìç´╝îµ£║ÕÖ¿Õ¡ªõ╣áµèǵ£»Õ¥ùÕê░õ║åÕ╣┐µ│øÕ║öþö¿´╝îõ¥ïÕªéÞç¬Õè¿Ú®¥Ú®Âµ▒¢Þ¢ªÒÇüÞ»¡Úƒ│Þ»åÕê½ÒÇüµÉ£þ┤óÕ╝òµôÄõ╝ÿÕîûþ¡ëÒÇé ##### 1.3 þøæþØúÕ¡ªõ╣á þøæþØúÕ¡ªõ╣áµÿ»õ©ÇþºìÕ©©ÞºüþÜäµ£║ÕÖ¿Õ¡ªõ╣áµû╣µ│ò´╝îÕ«âÚÇÜÞ┐çÞ«¡þ╗âÚøåõ©¡þÜäÞ¥ôÕàÑ...
Õ»╝µò░Úâ¿Õêåµÿ»ÒÇèThe matrix cookbook.pdfÒÇïþÜäÚçìÞªüÕåàÕ«╣õ╣ïõ©Ç´╝îÞ┐ÖÚâ¿ÕêåÞ»ªþ╗åÕ£░õ╗ïþ╗ìõ║åþƒ®ÚÿÁÕ碵ò░þÜäÕ»╝µò░´╝îÕîàµï¼ÞíîÕêùÕ╝ÅþÜäÕ»╝µò░ÒÇüÚÇåþƒ®ÚÿÁþÜäÕ»╝µò░ÒÇüþë╣Õ¥üÕÇ╝þÜäÕ»╝µò░õ╗ÑÕÅèþƒ®ÚÿÁÒÇüÕÉæÚçÅÕÆîµáçÚçÅÕ¢óÕ╝ÅþÜäÕ»╝µò░ÒÇéÞ┐Öõ║øÕåàÕ«╣Õ»╣õ║ĵò░Õ¡ªÒÇüþë®þÉåÕ¡ªÒÇüÕÀÑþ¿ïÕ¡ªÒÇü...
ÞÇîÞíîÕêùÕ╝ŵÿ»ÞííÚçÅþƒ®ÚÿÁÕÅ»ÚÇåµÇºþÜäµîçµáçÒÇé **5.9 µ£ÇÕ░Åõ║îõ╣ÿµïƒÕÉêÕÅèQRÕêåÞºú** µ£ÇÕ░Åõ║îõ╣ÿµïƒÕÉêµÿ»Õø×Õ¢ÆÕêåµ×Éõ©¡Õ©©þö¿þÜäµû╣µ│ò´╝îQRÕêåÞºúÕêÖµÿ»õ©Çþºìþƒ®ÚÿÁÕêåÞºúµèǵ£»´╝îÕ©©þö¿õ║ÄÞºúÕå│µ£ÇÕ░Åõ║îõ╣ÿÚù«ÚóÿÒÇé **5.10 µ×äÕ╗║ÕêåÕî║þƒ®ÚÿÁ´╝îcbind()ÕÆîrbind()** `...
ÞíîÕêùÕ╝ŵÿ»ÞííÚçÅþƒ®ÚÿÁÕÅ»ÚÇåµÇºþÜäµîçµáçÒÇé ##### 5.9 µ£ÇÕ░Åõ║îõ╣ÿµïƒÕÉêÕÅèQRÕêåÞºú µ£ÇÕ░Åõ║îõ╣ÿµïƒÕÉêµÿ»õ©ÇþºìÕ©©þö¿þÜäÕø×Õ¢ÆÕêåµ×ɵû╣µ│ò´╝îþö¿õ║Äõ╝░Þ«íµ£¬þƒÑÕÅéµò░þÜäµ£Çõ¢│õ╝░Þ«íÕÇ╝ÒÇéQRÕêåÞºúµÿ»ÕŪõ©Çþºìþƒ®ÚÿÁÕêåÞºúµû╣µ│ò´╝îÕ©©þö¿õ║ĵ▒éÞºúþ║┐µÇºµû╣þ¿ïþ╗äÒÇé ##### 5.10 µ×äÕ╗║...
2. Õ╝áÚçÅÞ┐Éþ«ù´╝ÜÕîàµï¼Õƒ║µ£¼þÜäµò░Õ¡ªÞ┐Éþ«ù´╝êÕèáµ│òÒÇüÕçŵ│òÒÇüõ╣ÿµ│òÒÇüÚÖñµ│ò´╝ëõ╗ÑÕÅèþƒ®ÚÿÁÞ┐Éþ«ù´╝êÞ¢¼þ¢«ÒÇüµ▒éÚÇåÒÇüµ▒éÞíîÕêùÕ╝Å´╝ëÒÇéÞ┐Öõ║øÞ┐Éþ«ùµÿ»µ×äÕ╗║µÀ▒Õ║ªÕ¡ªõ╣ᵿíÕ×ïþÜäÕƒ║þíÇÒÇé 3. µ¿íÕ×ïµ×äÕ╗║´╝ÜTensor 2.xµö»µîüÕ«Üõ╣ëÕÆîµ×äÕ╗║ÕñìµØéþÜäþÑ×þ╗Åþ¢æþ╗£þ╗ôµ×ä´╝îÕîàµï¼ÕìÀþº»þÑ×þ╗Å...