POJ 2663 Tri Tiling

Description

In how many ways can you tile a 3xn rectangle with 2x1 dominoes? 
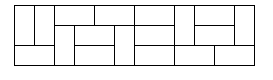
Here is a sample tiling of a 3x12 rectangle. 

Input

Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 <= n <= 30.

Output

For each test case, output one integer number giving the number of possible tilings.

Sample Input

2
8
12
-1

Sample Output

3
153
2131

Source

Waterloo local 2005.09.24

 

动态规划的一道题

根据Stanford CS97SI课件

 

 

 

 

 

根据本图，我们可以列出 D(n)=D(n-2)+2*A(n-1) 
 

 

 然后我们再分析 A(n)的情况： 

 可以得到：有两种排列方式

A(n)=D(n-1)+C(n-1)

 

 再分析C(n):

可得：

C(n)=A(n-1)
 

所以，我们有3个公式：

D(n)=D(n-2)+2*A(n-1) 

A(n)=D(n-1)+C(n-1)

C(n)=A(n-1)

 

化简第一个公式得：

D(n)=D(n-2)+2*A(n-1) 

= D(n-2)+2*(D(n-2)+C(n-2))

= D(n-2)+2*(D(n-2)+A(n-3))

= 3*D(n-2)+2*A(n-3)

= 3*D(n-2)+2*(D(n-4)+C(n-4))

= 3*D(n-2)+2*D(n-4)+2*C(n-4)

= 3*D(n-2)+2*D(n-4)+2*A(n-5)

= 3*D(n-2)+2*D(n-4)+2*(D(n-6)+C(n-6))

= 3*D(n-2)+2*D(n-4)+2*D(n-6)+2*C(n-6)

= 。。。

 

其中base case有：

D(0)=1, D(2)=3

 

#define RUN
#ifdef RUN

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>
#include <string>
#include <iostream>
#include <sstream>
#include <map>
#include <set>
#include <vector>
#include <list>
#include <cctype> 
#include <algorithm>
#include <utility>
#include <math.h>

using namespace std;


int n;
int buf[31];

int main(){

	memset(buf, sizeof(buf), 0);
	buf[0] = 1;
	buf[2] = 3;

	while(scanf("%d",&n)==1 && n!=-1){
		if(n%2 != 0){
			printf("0\n");
			continue;
		}

		for(int i=4; i<=n; i+=2){
			int tmp = 3*buf[i-2];
			for(int j=4; j<=i; j+=2){
				tmp += 2*buf[i-j];
			}
			buf[i] = tmp;
		}

		printf("%d\n", buf[n]);
	}
	
}


#endif