POJ 1966 Cable TV Network （EK 最小割）

 

Cable TV Network

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 3442		Accepted: 1602

Description

The interconnection of the relays in a cable TV network is bi-directional. The network is connected if there is at least one interconnection path between each pair of relays present in the network. Otherwise the network is disconnected. An empty network or a network with a single relay is considered connected. The safety factor f of a network with n relays is: 
1. n, if the net remains connected regardless the number of relays removed from the net. 
2. The minimal number of relays that disconnect the network when removed.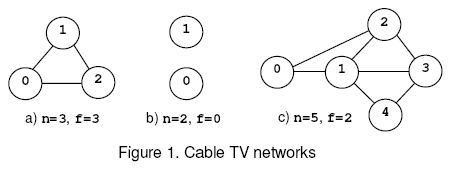 

For example, consider the nets from figure 1, where the circles mark the relays and the solid lines correspond to interconnection cables. The network (a) is connected regardless the number of relays that are removed and, according to rule (1), f=n=3. The network (b) is disconnected when 0 relays are removed, hence f=0 by rule (2). The network (c) is disconnected when the relays 1 and 2 or 1 and 3 are removed. The safety factor is 2.

Input

Write a program that reads several data sets from the standard input and computes the safety factor for the cable networks encoded by the data sets. Each data set starts with two integers: 0<=n<=50,the number of relays in the net, and m, the number of cables in the net. Follow m data pairs (u,v), u < v, where u and v are relay identifiers (integers in the range 0..n-1). The pair (u,v) designates the cable that interconnects the relays u and v. The pairs may occur in any order.Except the (u,v) pairs, which do not contain white spaces, white spaces can occur freely in input. Input data terminate with an end of file and are correct.

Output

For each data set, the program prints on the standard output, from the beginning of a line, the safety factor of the encoded net.

Sample Input

0 0
1 0
3 3 (0,1) (0,2) (1,2)
2 0
5 7 (0,1) (0,2) (1,3) (1,2) (1,4) (2,3) (3,4)

Sample Output

0
1
3
0
2

Hint

The first data set encodes an empty network, the second data set corresponds to a network with a single relay, and the following three data sets encode the nets shown in figure 1.

Source

Southeastern Europe 2004

 

 

题目大意：给你一个无向图，这个图有一个安全系数f，
f的定义是：
1.f为n，如果不管删除多少个顶点，剩下的图仍然是连通的
2.f为删除最少的顶点数，使得剩下的图不连通
给你一个图，求出f

解题思路:题目给出的目标很明显，转换成图，那么f就是无向图中的连通度吗，或者说，是求无向图中的最小割点集。
根据Menger定理，这样建图，首先将每个点拆成两个点
每个点可以表示成i与i+n

那么有向边<i,i+n>的容量为1
如果i与j相邻，那么有有向边<i+n,j>=<j+n,i>=INF，等于无穷大

然后固定源点，枚举汇点求最大流。如果最大流都是INF，那么代表这个图是一个完全连通图，最小割点集为n
否则就输出最大流。

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>

using namespace std;

const int VM=110;
const int EM=1010;
const int INF=0x3f3f3f3f;

int map[VM][VM],flow[VM][VM],pre[VM];   //pre[]用于bfs寻找路径

int BFS(int n,int src,int des){
    int res[VM];
    queue<int> q;
    while(!q.empty())
        q.pop();
    memset(res,0,sizeof(res));  //记录增广路最小流量，而且又可以当做广搜的标记数组  
    memset(pre,-1,sizeof(pre)); //记录下这条增广路，以便增流 
    q.push(src);
    res[src]=INF;
    while(!q.empty()){
        int u=q.front();
        q.pop();
        for(int i=0;i<n;i++)
            if(!res[i] && map[u][i]>flow[u][i]){    //如果这是一条允许弧就记录下来 
                q.push(i);
                pre[i]=u;
                res[i]=min(res[u],map[u][i]-flow[u][i]);
            }
        if(u==des)      //找到增广路退出
            break;
    }
    return res[des];
}

int EK(int n,int src,int des){
    int maxflow=0,tmp;
    memset(flow,0,sizeof(flow));
    while(tmp=BFS(n,src,des)){
        for(int i=des;i!=src;i=pre[i]){     //根据父亲数组更新流量
            flow[i][pre[i]]-=tmp;           //更新反向流
            flow[pre[i]][i]+=tmp;           //更新正向流 
        }
        maxflow+=tmp;
    }
    return maxflow;
}

int main(){

    //freopen("input.txt","r",stdin);

    int n,m;
    while(~scanf("%d%d",&n,&m)){
        memset(map,0,sizeof(map));
        for(int i=0;i<n;i++)
            map[i][i+n]=1;
        int u,v;
        for(int i=0;i<m;i++){
            scanf(" (%d,%d)",&u,&v);
            map[u+n][v]=map[v+n][u]=INF;
        }
        int ans=INF;
        for(int i=1;i<n;i++)
            ans=min(ans,EK(2*n,n,i));
        if(ans==INF)
            ans=n;
        printf("%d\n",ans);
    }
    return 0;
}