双数组-字典算法

转自双数组字典算法：<http://linux.thai.net/~thep/datrie/datrie.html>

An Implementation of Double-Array Trie

Contents

1. What is Trie?
2. What Does It Take to Implement a Trie?
3. Tripple-Array Trie
4. Double-Array Trie
5. Suffix Compression
6. Key Insertion
7. Key Deletion
8. Double-Array Pool Allocation
9. An Implementation
10. Download
11. Other Implementations
12. References

What is Trie?

Trie is a kind of digital search tree. (See [Knuth1972] for the detail of digital search tree.) [Fredkin1960] introduced the trie terminology, which is abbreviated from "Retrieval".

Trie is an efficient indexing method. It is indeed also a kind of deterministic finite automaton (DFA) (See [Cohen1990], for example, for the definition of DFA). Within the tree structure, each node corresponds to a DFA state, each (directed) labeled edge from a parent node to a child node corresponds to a DFA transition. The traversal starts at the root node. Then, from head to tail, one by one character in the key string is taken to determine the next state to go. The edge labeled with the same character is chosen to walk. Notice that each step of such walking consumes one character from the key and descends one step down the tree. If the key is exhausted and a leaf node is reached, then we arrive at the exit for that key. If we get stuck at some node, either because there is no branch labeled with the current character we have or because the key is exhausted at an internal node, then it simply implies that the key is not recognized by the trie.

Notice that the time needed to traverse from the root to the leaf is not dependent on the size of the database, but is proportional to the length of the key. Therefore, it is usually much faster than B-tree or any comparison-based indexing method in general cases. Its time complexity is comparable with hashing techniques.

In addition to the efficiency, trie also provides flexibility in searching for the closest path in case that the key is misspelled. For example, by skipping a certain character in the key while walking, we can fix the insertion kind of typo. By walking toward all the immediate children of one node without consuming a character from the key, we can fix the deletion typo, or even substitution typo if we just drop the key character that has no branch to go and descend to all the immediate children of the current node.

What Does It Take to Implement a Trie?

In general, a DFA is represented with a transition table, in which the rows correspond to the states, and the columns correspond to the transition labels. The data kept in each cell is then the next state to go for a given state when the input is equal to the label.

This is an efficient method for the traversal, because every transition can be calculated by two-dimensional array indexing. However, in term of space usage, this is rather extravagant, because, in the case of trie, most nodes have only a few branches, leaving the majority of the table cells blanks.

Meanwhile, a more compact scheme is to use a linked list to store the transitions out of each state. But this results in slower access, due to the linear search.

Hence, table compression techniques which still allows fast access have been devised to solve the problem.

1. [Johnson1975] (Also explained in [Aho+1985] pp. 144-146) represented DFA with four arrays, which can be simplified to three in case of trie. The transition table rows are allocated in overlapping manner, allowing the free cells to be used by other rows.
2. [Aoe1989] proposed an improvement from the three-array structure by reducing the arrays to two.

Tripple-Array Trie

As explained in [Aho+1985] pp. 144-146, a DFA compression could be done using four linear arrays, namely default, base, next, and check. However, in a case simpler than the lexical analyzer, such as the mere trie for information retrieval, the default array could be omitted. Thus, a trie can be implemented using three arrays according to this scheme.

Structure

The tripple-array structure is composed of:

1. base. Each element in base corresponds to a node of the trie. For a trie node s, base[s] is the starting index within the next and check pool (to be explained later) for the row of the node s in the transition table.
2. next. This array, in coordination with check, provides a pool for the allocation of the sparse vectors for the rows in the trie transition table. The vector data, that is, the vector of transitions from every node, would be stored in this array.
3. check. This array works in parallel to next. It marks the owner of every cell in next. This allows the cells next to one another to be allocated to different trie nodes. That means the sparse vectors of transitions from more than one node are allowed to be overlapped.

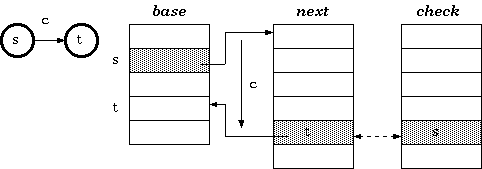
Definition 1. For a transition from state s to t which takes character c as the input, the condition maintained in the tripple-array trie is:

check[base[s] + c] = s
next[base[s] + c] = t

Walking

According to definition 1, the walking algorithm for a given state s and the input character c is:

t := base[s] + c;
if check[t] = s then next state := next[t] else fail endif

Construction

To insert a transition that takes character c to traverse from a state s to another state t, the cell next[base[s] + c]] must be managed to be available. If it is already vacant, we are lucky. Otherwise, either the entire transition vector for the current owner of the cell or that of the state s itself must be relocated. The estimated cost for each case could determine which one to move. After finding the free slots to place the vector, the transition vector must be recalculated as follows. Assuming the new place begins at b, the procedure for the relocation is:

Procedure Relocate(s : state; b : base_index) { Move base for state s to a new place beginning at b } begin foreach input character c for the state s { i.e. foreach c such that check[base[s] + c]] = s } begin check[b + c] := s; { mark owner } next[b + c] := next[base[s] + c]; { copy data } check[base[s] + c] := none { free the cell } end; base[s] := b end

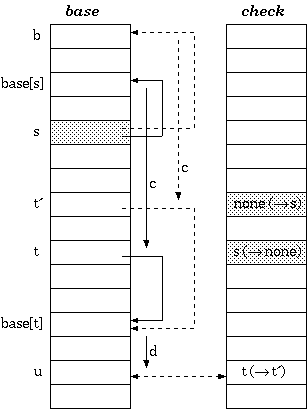
Double-Array Trie

The tripple-array structure for implementing trie appears to be well defined, but is still not practical to keep in a single file. The next/check pool may be able to keep in a single array of integer couples, but the base array does not grow in parallel to the pool, and is therefore usually split.

To solve this problem, [Aoe1989] reduced the structure into two parallel arrays. In the double-array structure, the base and next are merged, resulting in only two parallel arrays, namely, base and check.

Structure

Instead of indirectly referencing through state numbers as in tripple-array trie, nodes in double-array trie are linked directly within the base/check pool.

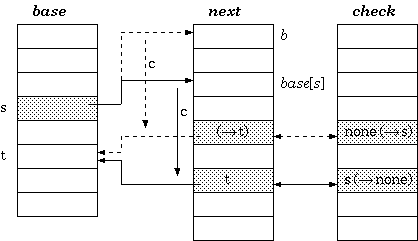
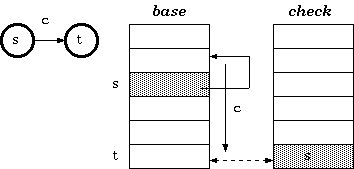
Definition 2. For a transition from state s to t which takes character c as the input, the condition maintained in the double-array trie is:

check[base[s] + c] = s
base[s] + c = t

Walking

According to definition 2, the walking algorithm for a given state s and the input character c is:

t := base[s] + c;
if check[t] = s then next state := t else fail endif

Construction

The construction of double-array trie is in principle the same as that of tripple-array trie. The difference is the base relocation:

Procedure Relocate(s : state; b : base_index) { Move base for state s to a new place beginning at b } begin foreach input character c for the state s { i.e. foreach c such that check[base[s] + c]] = s } begin check[b + c] := s; { mark owner } base[b + c] := base[base[s] + c]; { copy data } { the node base[s] + c is to be moved to b + c; Hence, for any i for which check[i] = base[s] + c, update check[i] to b + c } foreach input character d for the node base[s] + c begin check[base[base[s] + c] + d] := b + c end; check[base[s] + c] := none { free the cell } end; base[s] := b end

Suffix Compression

[Aoe1989] also suggested a storage compression strategy, by splitting non-branching suffixes into single string storages, called tail, so that the rest non-branching steps are reduced into mere string comparison.

With the two separate data structures, double-array branches and suffix-spool tail, key insertion and deletion algorithms must be modified accordingly.

Key Insertion

To insert a new key, the branching position can be found by traversing the trie with the key one by one character until it gets stuck. The state where there is no branch to go is the very place to insert a new edge, labeled by the failing character. However, with the branch-tail structure, the insertion point can be either in the branch or in the tail.

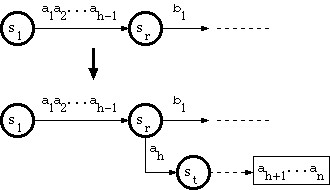
1. When the branching point is in the double-array structure

Suppose that the new key is a string a₁a₂...a_h-1a_ha_h+1...a_n, where a₁a₂...a_h-1 traverses the trie from the root to a node s_r in the double-array structure, and there is no edge labeled a_h that goes out of s_r. The algorithm called A_INSERT in [Aoe1989] does as follows:

From s_r, insert edge labeled a_h to new node s_t; Let s_t be a separate node poining to a string a_h+1...a_n in tail pool.

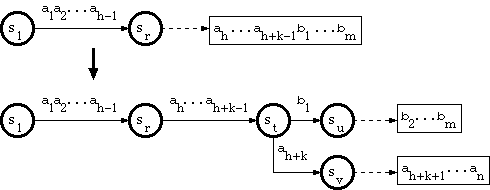
2. When the branching point is in the tail pool

Since the path through a tail string has no branch, and therefore corresponds to exactly one key, suppose that the key corresponding to the tail is

a₁a₂...a_h-1a_h...a_h+k-1b₁...b_m,

where a₁a₂...a_h-1 is in double-array structure, and a_h...a_h+k-1b₁...b_m is in tail. Suppose that the substring a₁a₂...a_h-1 traverses the trie from the root to a node s_r.

And suppose that the new key is in the form

a₁a₂...a_h-1a_h...a_h+k-1a_h+k...a_n,

where a_h+k <> b₁. The algorithm called B_INSERT in [Aoe1989] does as follows:

From s_r, insert straight path with a_h...a_h+k-1, ending at a new node s_t; From s_t, insert edge labeled b₁ to new node s_u; Let s_u be separate node pointing to a string b₂...b_m in tail pool; From s_t, insert edge labeled a_h+k to new node s_v; Let s_v be separate node pointing to a string a_h+k+1...a_n in tail pool.

Key Deletion

To delete a key from the trie, all we need to do is delete the tail block occupied by the key, and all double-array nodes belonging exclusively to the key, without touching any node belonging to other keys.

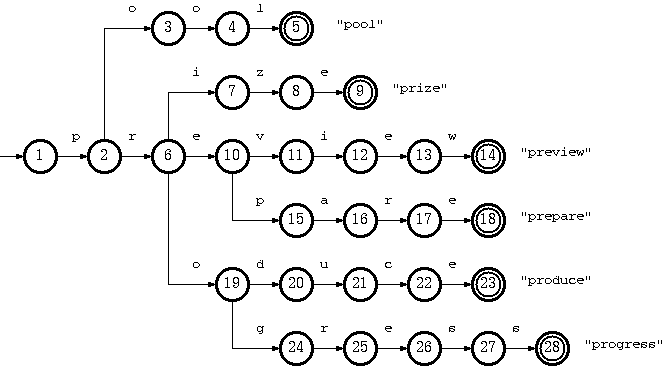
Consider a trie which accepts a language K = {pool#, prepare#, preview#, prize#, produce#, producer#, progress#} :

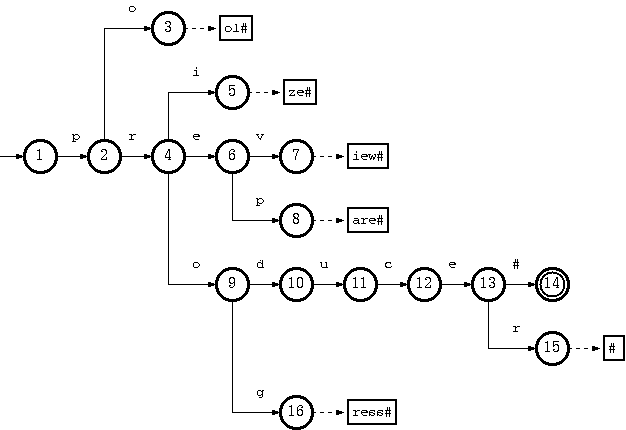
The key "pool#" can be deleted by removing the tail string "ol#" from the tail pool, and node 3 from the double-array structure. This is the simplest case.

To remove the key "produce#", it is sufficient to delete node 14 from the double-array structure. But the resulting trie will not obay the convention that every node in the double-array structure, except the separate nodes which point to tail blocks, must belong to more than one key. The path from node 10 on will belong solely to the key "producer#".

But there is no harm violating this rule. The only drawback is the uncompactnesss of the trie. Traversal, insertion and deletion algoritms are intact. Therefore, this should be relaxed, for the sake of simplicity and efficiency of the deletion algorithm. Otherwise, there must be extra steps to examine other keys in the same subtree ("producer#" for the deletion of "produce#") if any node needs to be moved from the double-array structure to tail pool.

Suppose further that having removed "produce#" as such (by removing only node 14), we also need to remove "producer#" from the trie. What we have to do is remove string "#" from tail, and remove nodes 15, 13, 12, 11, 10 (which now belong solely to the key "producer#") from the double-array structure.

We can thus summarize the algorithm to delete a key k = a₁a₂...a_h-1a_h...a_n, where a₁a₂...a_h-1 is in double-array structure, and a_h...a_n is in tail pool, as follows :

Let s_r := the node reached by a₁a₂...a_h-1; Delete a_h...a_n from tail; s := s_r; repeat p := parent of s; Delete node s from double-array structure; s := p until s = root or outdegree(s) > 0.

Where outdegree(s) is the number of children nodes of s.

Double-Array Pool Allocation

When inserting a new branch for a node, it is possible that the array element for the new branch has already been allocated to another node. In that case, relocation is needed. The efficiency-critical part then turns out to be the search for a new place. A brute force algoritm iterates along the check array to find an empty cell to place the first branch, and then assure that there are empty cells for all other branches as well. The time used is therefore proportional to the size of the double-array pool and the size of the alphabet.

Suppose that there are n nodes in the trie, and the alphabet is of size m. The size of the double-array structure would be n + cm, where c is a coefficient which is dependent on the characteristic of the trie. And the time complexity of the brute force algorithm would be O(nm + cm²).

[Aoe1989] proposed a free-space list in the double-array structure to make the time complexity independent of the size of the trie, but dependent on the number of the free cells only. The check array for the free cells are redefined to keep a pointer to the next free cell (called G-link) :

Definition 3. Let r₁, r₂, ... , r_cm be the free cells in the double-array structure, ordered by position. G-link is defined as follows :

check[0] = -r₁
check[r_i] = -r_i+1 ; 1 <= i <= cm-1
check[r_cm] = -1

By this definition, negative check means unoccupied in the same sense as that for "none" check in the ordinary algorithm. This encoding scheme forms a singly-linked list of free cells. When searching for an empty cell, only cm free cells are visited, instead of all n + cm cells as in the brute force algorithm.

This, however, can still be improved. Notice that for those cells with negative check, the corresponding base's are not given any definition. Therefore, in our implementation, Aoe's G-link is modified to be doubly-linked list by letting base of every free cell points to a previous free cell. This can speed up the insertion and deletion processes. And, for convenience in referencing the list head and tail, we let the list be circular. The zeroth node is dedicated to be the entry point of the list. And the root node of the trie will begin with cell number one.

Definition 4. Let r₁, r₂, ... , r_cm be the free cells in the double-array structure, ordered by position. G-link is defined as follows :

check[0] = -r₁
check[r_i] = -r_i+1 ; 1 <= i <= cm-1
check[r_cm] = 0
base[0] = -r_cm
base[r₁] = 0
base[r_i+1] = -r_i ; 1 <= i <= cm-1

Then, the searching for the slots for a node with input symbol set P = {c₁, c₂, ..., c_p} needs to iterate only the cells with negative check :

{find least free cell s such that s > c₁} s := -check[0]; while s <> 0 and s <= c₁do s := -check[s] end; if s = 0 then return FAIL; {or reserve some additional space} {continue searching for the row, given that s matches c₁} while s <> 0 do i := 2; while i <= p and check[s + c_i - c₁] < 0 do i := i + 1 end; if i = p + 1 then return s - c₁; {all cells required are free, so return it} s := -check[s] end; return FAIL; {or reserve some additional space}

The time complexity for free slot searching is reduced to O(cm²). The relocation stage takes O(m²). The total time complexity is therefore O(cm² + m²) = O(cm²).

It is useful to keep the free list ordered by position, so that the access through the array becomes more sequential. This would be beneficial when the trie is stored in a disk file or virtual memory, because the disk caching or page swapping would be used more efficiently. So, the free cell reusing should maintain this strategy :

t := -check[0]; while check[t] <> 0 and t < s do t := -check[t] end; {t now points to the cell after s' place} check[s] := -t; check[-base[t]] := -s; base[s] := base[t]; base[t] := -s;

Time complexity of freeing a cell is thus O(cm).

An Implementation

In my implementation, I designed the API with persistent data in mind. Tries can be saved to disk and loaded for use afterward. And in newer versions, non-persistent usage is also possible. You can create a trie in memory, populate data to it, use it, and free it, without any disk I/O. Alternatively you can load a trie from disk and save it to disk whenever you want.

The trie data is portable across platforms. The byte order in the disk is always little-endian, and is read correctly on either little-endian or big-endian systems.

Trie index is 32-bit signed integer. This allows 2,147,483,646 (2³¹ - 2) total nodes in the trie data, which should be sufficient for most problem domains. And each data entry can store a 32-bit integer value associated to it. This value can be used for any purpose, up to your needs. If you don't need to use it, just store some dummy value.

For sparse data compactness, the trie alphabet set should be continuous, but that is usually not the case in general character sets. Therefore, a map between the input character and the low-level alphabet set for the trie is created in the middle. You will have to define your input character set by listing their continuous ranges of character codes in a .abm (alphabet map) file when creating a trie. Then, each character will be automatically assigned internal codes of continuous values.

Download

Update: The double-array trie implementation has been simplified and rewritten from scratch in C, and is now named libdatrie. It is now available under the terms of GNU Lesser General Public License (LGPL):

• libdatrie-0.2.4 (30 June 2010)
• libdatrie-0.2.3 (27 February 2010)
• libdatrie-0.2.2 (29 April 2009)
• libdatrie-0.2.1 (5 April 2009)
• libdatrie-0.2.0 (24 March 2009)
• libdatrie-0.1.3 (28 January 2008)
• libdatrie-0.1.2 (25 August 2007)
• libdatrie-0.1.1 (12 October 2006)
• libdatrie-0.1.0 (18 September 2006)

SVN: svn co http://linux.thai.net/svn/software/datrie

The old C++ source code below is under the terms of GNU Lesser General Public License (LGPL):

• midatrie-0.3.3 (2 October 2001)
• midatrie-0.3.3 (16 July 2001)
• midatrie-0.3.2 (21 May 2001)
• midatrie-0.3.1 (8 May 2001)
• midatrie-0.3.0 (23 Mar 2001)

Other Implementations

• DoubleArrayTrie: Java implementation by Christos Gioran (More information)

References

1. [Knuth1972] Knuth, D. E. The Art of Computer Programming Vol. 3, Sorting and Searching. Addison-Wesley. 1972.
2. [Fredkin1960] Fredkin, E. Trie Memory. Communication of the ACM. Vol. 3:9 (Sep 1960). pp. 490-499.
3. [Cohen1990] Cohen, D. Introduction to Theory of Computing. John Wiley & Sons. 1990.
4. [Johnson1975] Johnson, S. C. YACC-Yet another compiler-compiler. Bell Lab. NJ. Computing Science Technical Report 32. pp.1-34. 1975.
5. [Aho+1985] Aho, A. V., Sethi, R., Ullman, J. D. Compilers : Principles, Techniques, and Tools. Addison-Wesley. 1985.
6.  [Aoe1989] Aoe, J. An Efficient Digital Search Algorithm by Using a Double-Array Structure. IEEE Transactions on Software Engineering. Vol. 15, 9 (Sep 1989). pp. 1066-1077.
7.  [Virach+1993] Virach Sornlertlamvanich, Apichit Pittayaratsophon, Kriangchai Chansaenwilai. Thai Dictionary Data Base Manipulation using Multi-indexed Double Array Trie. 5th Annual Conference. National Electronics and Computer Technology Center. Bangkok. 1993. pp 197-206. (in Thai)

---

Theppitak Karoonboonyanan Created: 1999-06-13 Last Updated 2012-12-02 Back to Theppitak's Homepage

Copyright © 1999 by Theppitak Karoonboonyanan, Software and Language Engineering Laboratory, National Electronics and Computer Technology Center. All rights reserved.

Copyright © 2003-2010 by Theppitak Karoonboonyanan. All rights reserved.