遍历二叉树的各种操作（非递归遍历）

更多二叉树的操作见http://blog.csdn.net/Hackbuteer1/article/details/6686858

http://blog.csdn.net/Hackbuteer1/article/details/8022138

先使用先序的方法建立一棵二叉树，然后分别使用递归与非递归的方法实现前序、中序、后序遍历二叉树，并使用了两种方法来进行层次遍历二叉树，一种方法就是使用STL中的queue，另外一种方法就是定义了一个数组队列，分别使用了front和rear两个数组的下标来表示入队与出队，还有两个操作就是求二叉树的深度、结点数。。。

#include<iostream>
#include<queue>
#include<stack>
usingnamespacestd;

//二叉树结点的描述
typedefstructBiTNode
{
chardata;
structBiTNode*lchild,*rchild;//左右孩子
}BiTNode,*BiTree;

//按先序遍历创建二叉树
//BiTree*CreateBiTree()//返回结点指针类型
//voidCreateBiTree(BiTree&root)//引用类型的参数
voidCreateBiTree(BiTNode**root)//二级指针作为函数参数
{
charch;//要插入的数据
scanf("\n%c",&ch);
//cin>>ch;
if(ch=='#')
*root=NULL;
else
{
*root=(BiTNode*)malloc(sizeof(BiTNode));
(*root)->data=ch;
printf("请输入%c的左孩子：",ch);
CreateBiTree(&((*root)->lchild));
printf("请输入%c的右孩子：",ch);
CreateBiTree(&((*root)->rchild));
}
}

//前序遍历的算法程序
voidPreOrder(BiTNode*root)
{
if(root==NULL)
return;
printf("%c",root->data);//输出数据
PreOrder(root->lchild);//递归调用，前序遍历左子树
PreOrder(root->rchild);//递归调用，前序遍历右子树
}

//中序遍历的算法程序
voidInOrder(BiTNode*root)
{
if(root==NULL)
return;
InOrder(root->lchild);//递归调用，前序遍历左子树
printf("%c",root->data);//输出数据
InOrder(root->rchild);//递归调用，前序遍历右子树
}

//后序遍历的算法程序
voidPostOrder(BiTNode*root)
{
if(root==NULL)
return;
PostOrder(root->lchild);//递归调用，前序遍历左子树
PostOrder(root->rchild);//递归调用，前序遍历右子树
printf("%c",root->data);//输出数据
}

/*
二叉树的非递归前序遍历，前序遍历思想：先让根进栈，只要栈不为空，就可以做弹出操作，
每次弹出一个结点，记得把它的左右结点都进栈，记得右子树先进栈，这样可以保证右子树在栈中总处于左子树的下面。
*/
voidPreOrder_Nonrecursive2(BiTreeT)//先序遍历的非递归
{
if(!T)
return;

stack<BiTree>s;
s.push(T);

while(!s.empty())
{
BiTreetemp=s.top();
cout<<temp->data<<"";
s.pop();
if(temp->rchild)
s.push(temp->rchild);
if(temp->lchild)
s.push(temp->lchild);
}
}


voidPreOrder_Nonrecursive(BiTreeT)//先序遍历的非递归
{
if(!T)
return;

stack<BiTree>s;
while(T)//左子树上的节点全部压入到栈中
{
s.push(T);
cout<<T->data<<"";
T=T->lchild;
}

while(!s.empty())
{
BiTreetemp=s.top()->rchild;//栈顶元素的右子树
s.pop();//弹出栈顶元素
while(temp)//栈顶元素存在右子树，则对右子树同样遍历到最下方
{
cout<<temp->data<<"";
s.push(temp);
temp=temp->lchild;
}
}
}

voidInOrderTraverse(BiTreeT)//中序遍历的非递归
{
if(!T)
return;
stack<BiTree>S;
BiTreecurr=T->lchild;//指向当前要检查的节点
S.push(T);
while(curr!=NULL||!S.empty())
{
while(curr!=NULL)//一直向左走
{
S.push(curr);
curr=curr->lchild;
}
curr=S.top();
S.pop();
cout<<curr->data<<"";
curr=curr->rchild;
}
}

voidPostOrder_Nonrecursive(BiTreeT)//后序遍历的非递归
{
stack<BiTree>S;
BiTreecurr=T;//指向当前要检查的节点
BiTreeprevisited=NULL;//指向前一个被访问的节点
while(curr!=NULL||!S.empty())//栈空时结束
{
while(curr!=NULL)//一直向左走直到为空
{
S.push(curr);
curr=curr->lchild;
}
curr=S.top();
//当前节点的右孩子如果为空或者已经被访问，则访问当前节点
if(curr->rchild==NULL||curr->rchild==previsited)
{
cout<<curr->data<<"";
previsited=curr;
S.pop();
curr=NULL;
}
else
curr=curr->rchild;//否则访问右孩子
}
}

voidPostOrder_Nonrecursive(BiTreeT)//后序遍历的非递归双栈法
{
stack<BiTree>s1,s2;
BiTreecurr;//指向当前要检查的节点
s1.push(T);
while(!s1.empty())//栈空时结束
{
curr=s1.top();
s1.pop();
s2.push(curr);
if(curr->lchild)
s1.push(curr->lchild);
if(curr->rchild)
s1.push(curr->rchild);
}
while(!s2.empty())
{
printf("%c",s2.top()->data);
s2.pop();
}
}


intvisit(BiTreeT)
{
if(T)
{
printf("%c",T->data);
return1;
}
else
return0;
}

voidLeverTraverse(BiTreeT)//方法一、非递归层次遍历二叉树
{
queue<BiTree>Q;
BiTreep;
p=T;
if(visit(p)==1)
Q.push(p);
while(!Q.empty())
{
p=Q.front();
Q.pop();
if(visit(p->lchild)==1)
Q.push(p->lchild);
if(visit(p->rchild)==1)
Q.push(p->rchild);
}
}
voidLevelOrder(BiTreeBT)//方法二、非递归层次遍历二叉树
{
BiTNode*queue[10];//定义队列有十个空间
if(BT==NULL)
return;
intfront,rear;
front=rear=0;
queue[rear++]=BT;
while(front!=rear)//如果队尾指针不等于对头指针时
{
cout<<queue[front]->data<<"";//输出遍历结果
if(queue[front]->lchild!=NULL)//将队首结点的左孩子指针入队列
{
queue[rear]=queue[front]->lchild;
rear++;//队尾指针后移一位
}
if(queue[front]->rchild!=NULL)
{
queue[rear]=queue[front]->rchild;//将队首结点的右孩子指针入队列
rear++;//队尾指针后移一位
}
front++;//对头指针后移一位
}
}

intdepth(BiTNode*T)//树的深度
{
if(!T)
return0;
intd1,d2;
d1=depth(T->lchild);
d2=depth(T->rchild);
return(d1>d2?d1:d2)+1;
//return(depth(T->lchild)>depth(T->rchild)?depth(T->lchild):depth(T->rchild))+1;
}
intCountNode(BiTNode*T)
{
if(T==NULL)
return0;
return1+CountNode(T->lchild)+CountNode(T->rchild);
}

intmain(void)
{
BiTNode*root=NULL;//定义一个根结点
intflag=1,k;
printf("本程序实现二叉树的基本操作。\n");
printf("可以进行建立二叉树，递归先序、中序、后序遍历，非递归先序、中序遍历及非递归层序遍历等操作。\n");

while(flag)
{
printf("\n");
printf("|--------------------------------------------------------------|\n");
printf("|二叉树的基本操作如下:|\n");
printf("|0.创建二叉树|\n");
printf("|1.递归先序遍历|\n");
printf("|2.递归中序遍历|\n");
printf("|3.递归后序遍历|\n");
printf("|4.非递归先序遍历|\n");
printf("|5.非递归中序遍历|\n");
printf("|6.非递归后序遍历|\n");
printf("|7.非递归层序遍历|\n");
printf("|8.二叉树的深度|\n");
printf("|9.二叉树的结点个数|\n");
printf("|10.退出程序|\n");
printf("|--------------------------------------------------------------|\n");
printf("请选择功能：");
scanf("%d",&k);
switch(k)
{
case0:
printf("请建立二叉树并输入二叉树的根节点：");
CreateBiTree(&root);
break;
case1:
if(root)
{
printf("递归先序遍历二叉树的结果为：");
PreOrder(root);
printf("\n");
}
else
printf("二叉树为空！\n");
break;
case2:
if(root)
{
printf("递归中序遍历二叉树的结果为：");
InOrder(root);
printf("\n");
}
else
printf("二叉树为空！\n");
break;
case3:
if(root)
{
printf("递归后序遍历二叉树的结果为：");
PostOrder(root);
printf("\n");
}
else
printf("二叉树为空！\n");
break;
case4:
if(root)
{
printf("非递归先序遍历二叉树：");
PreOrder_Nonrecursive(root);
printf("\n");
}
else
printf("二叉树为空！\n");
break;
case5:
if(root)
{
printf("非递归中序遍历二叉树：");
InOrderTraverse(root);
printf("\n");
}
else
printf("二叉树为空！\n");
break;
case6:
if(root)
{
printf("非递归后序遍历二叉树：");
PostOrder_Nonrecursive(root);
printf("\n");
}
else
printf("二叉树为空！\n");
break;
case7:
if(root)
{
printf("非递归层序遍历二叉树：");
//LeverTraverse(root);
LevelOrder(root);
printf("\n");
}
else
printf("二叉树为空！\n");
break;
case8:
if(root)
printf("这棵二叉树的深度为：%d\n",depth(root));
else
printf("二叉树为空！\n");
break;
case9:
if(root)
printf("这棵二叉树的结点个数为：%d\n",CountNode(root));
else
printf("二叉树为空！\n");
break;
default:
flag=0;
printf("程序运行结束，按任意键退出！\n");
}
}
system("pause");
return0;
}

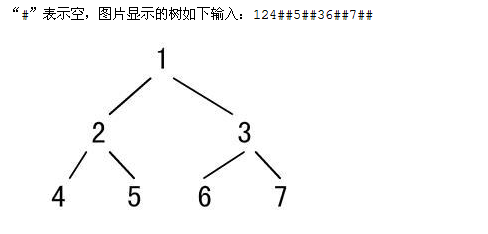
运行效果图如下：

分别输入：

1

2

4

#

#

5

#

#

3

6

#

#

7

#

#

就可以构造如下图所示的二叉树了。。

后序遍历非递归的另外一种写法：

 

/*
后序遍历由于遍历父节点是在遍历子节点之后，而且左节点和右节点遍历后的行为不一样，
所以需要用变量来记录前一次访问的节点，根据前一次节点和现在的节点的关系来确定具体执行什么操作
*/
voidPostorder(BiTreeT)
{
if(T==NULL)
return;
stack<BiTree>s;
BiTreeprev=NULL,curr=NULL;
s.push(T);
while(!s.empty())
{
curr=s.top();
if(prev==NULL||prev->lchild==curr||prev->rchild==curr)
{
if(curr->lchild!=NULL)
s.push(curr->lchild);
elseif(curr->rchild!=NULL)
s.push(curr->rchild);
}
elseif(curr->lchild==prev)
{
if(curr->rchild!=NULL)
s.push(curr->rchild);
}
else
{
cout<<curr->data;
s.pop();
}
prev=curr;
}
}

输入二叉树中的两个节点，输出这两个结点在数中最低的共同父节点。
思路：遍历二叉树，找到一条从根节点开始到目的节点的路径，然后在两条路径上查找共同的父节点。

//得到一条从根节点开始到目的节点的路径
boolGetNodePath(TreeNode*pRoot,TreeNode*pNode,vector<TreeNode*>&path)
{
if(pRoot==NULL)
returnfalse;
if(pRoot==pNode)
returntrue;
elseif(GetNodePath(pRoot->lchild,pNode,path))
{
path.push_back(pRoot->lchild);
returntrue;
}
elseif(GetNodePath(pRoot->rchild,pNode,path))
{
path.push_back(pRoot->rchild);
returntrue;
}
returnfalse;
}
TreeNode*GetLastCommonNode(constvector<TreeNode*>&path1,constvector<TreeNode*>&path2)
{
vector<TreeNode*>::const_iteratoriter1=path1.begin();
vector<TreeNode*>::const_iteratoriter2=path2.begin();
TreeNode*pLast;
while(iter1!=path1.end()&&iter2!=path2.end())
{
if(*iter1==*iter2)
pLast=*iter1;
else
break;
iter1++;
iter2++;
}
returnpLast;
}
TreeNode*GetLastCommonParent(TreeNode*pRoot,TreeNode*pNode1,TreeNode*pNode2)
{
if(pRoot==NULL||pNode1==NULL||pNode2==NULL)
returnNULL;
vector<TreeNode*>path1;
GetNodePath(pRoot,pNode1,path1);

vector<TreeNode*>path2;
GetNodePath(pRoot,pNode2,path2);
returnGetLastCommonNode(path1,path2);
}