1 ه½’ه¹¶وژ’ه؛ڈ(MergeSort)
ه½’ه¹¶وژ’ه؛ڈوœ€ه·®è؟گè،Œو—¶é—´وک¯O(nlogn),ه®ƒوک¯هˆ©ç”¨é€’ه½’设è®،程ه؛ڈçڑ„ه…¸ه‹ن¾‹هگم€‚
ه½’ه¹¶وژ’ه؛ڈçڑ„وœ€هں؛ç،€çڑ„و“چن½œه°±وک¯هگˆه¹¶ن¸¤ن¸ھه·²ç»ڈوژ’ه¥½ه؛ڈçڑ„ه؛ڈهˆ—م€‚
هپ‡è®¾وˆ‘ن»¬وœ‰ن¸€ن¸ھو²،وœ‰وژ’ه¥½ه؛ڈçڑ„ه؛ڈهˆ—,那ن¹ˆé¦–ه…ˆوˆ‘ن»¬ن½؟用هˆ†ه‰²çڑ„هٹو³•ه°†è؟™ن¸ھه؛ڈهˆ—هˆ†ه‰²وˆگن¸€ن¸ھن¸€ن¸ھه·²ç»ڈوژ’ه¥½ه؛ڈçڑ„هگه؛ڈهˆ—م€‚然هگژه†چهˆ©ç”¨ه½’ه¹¶çڑ„و–¹و³•ه°†ن¸€ن¸ھن¸ھçڑ„هگه؛ڈهˆ—هگˆه¹¶وˆگوژ’ه؛ڈه¥½çڑ„ه؛ڈهˆ—م€‚هˆ†ه‰²ه’Œه½’ه¹¶çڑ„è؟‡ç¨‹هڈ¯ن»¥çœ‹ن¸‹é¢çڑ„ه›¾ن¾‹م€‚

ن»ژن¸ٹه›¾هڈ¯ن»¥çœ‹ه‡؛,وˆ‘ن»¬é¦–ه…ˆوٹٹن¸€ن¸ھوœھوژ’ه؛ڈçڑ„ه؛ڈهˆ—ن»ژن¸é—´هˆ†ه‰²وˆگ2部هˆ†ï¼Œه†چوٹٹ2部هˆ†هˆ†وˆگ4部هˆ†ï¼Œن¾و¬،هˆ†ه‰²ن¸‹هژ»ï¼Œç›´هˆ°هˆ†ه‰²وˆگن¸€ن¸ھن¸€ن¸ھçڑ„و•°وچ®ï¼Œه†چوٹٹè؟™ن؛›و•°وچ®ن¸¤ن¸¤ه½’ه¹¶هˆ°ن¸€èµ·ï¼Œن½؟ن¹‹وœ‰ه؛ڈ,ن¸چهپœçڑ„ه½’ه¹¶ï¼Œوœ€هگژوˆگن¸؛ن¸€ن¸ھوژ’ه¥½ه؛ڈçڑ„ه؛ڈهˆ—م€‚
ه¦‚ن½•وٹٹن¸¤ن¸ھه·²ç»ڈوژ’ه؛ڈه¥½çڑ„هگه؛ڈهˆ—ه½’ه¹¶وˆگن¸€ن¸ھوژ’ه¥½ه؛ڈçڑ„ه؛ڈهˆ—ه‘¢ï¼ںهڈ¯ن»¥هڈ‚看ن¸‹é¢çڑ„و–¹و³•م€‚
هپ‡è®¾وˆ‘ن»¬وœ‰ن¸¤ن¸ھه·²ç»ڈوژ’ه؛ڈه¥½çڑ„هگه؛ڈهˆ—م€‚
ه؛ڈهˆ—Aï¼ڑ1 23 34 65
ه؛ڈهˆ—Bï¼ڑ2 13 14 87
é‚£ن¹ˆهڈ¯ن»¥وŒ‰ç…§ن¸‹é¢çڑ„و¥éھ¤ه°†ه®ƒن»¬ه½’ه¹¶هˆ°ن¸€ن¸ھه؛ڈهˆ—ن¸م€‚
(1)首ه…ˆè®¾ه®ڑن¸€ن¸ھو–°çڑ„و•°هˆ—C[8]م€‚
(2)A[0]ه’ŒB[0]و¯”较,A[0] = 1,B[0] = 2,A[0] < B[0],那ن¹ˆC[0] = 1
(3)A[1]ه’ŒB[0]و¯”较,A[1] = 23,B[0] = 2,A[1]آ > B[0],那ن¹ˆC[1] = 2
(4)A[1]ه’ŒB[1]و¯”较,A[1] = 23,B[1] = 13,A[1]آ > B[1],那ن¹ˆC[2] = 13
(5)A[1]ه’ŒB[2]و¯”较,A[1] = 23,B[2] = 14,A[1]آ > B[2],那ن¹ˆC[3] = 14
(6)A[1]ه’ŒB[3]و¯”较,A[1] = 23,B[3] = 87,A[1] < B[3],那ن¹ˆC[4] = 23
(7)A[2]ه’ŒB[3]و¯”较,A[2] = 34,B[3] = 87,A[2] < B[3],那ن¹ˆC[5] = 34
(8)A[3]ه’ŒB[3]و¯”较,A[3] = 65,B[3] = 87,A[3] < B[3],那ن¹ˆC[6] = 65
(9)وœ€هگژه°†B[3]ه¤چهˆ¶هˆ°Cن¸ï¼Œé‚£ن¹ˆC[7] = 87م€‚ه½’ه¹¶ه®Œوˆگم€‚
ه¦‚وœوˆ‘ن»¬و¸…و¥ڑن؛†ن¸ٹé¢çڑ„هˆ†ه‰²ه’Œه½’ه¹¶è؟‡ç¨‹ï¼Œé‚£ن¹ˆوˆ‘ن»¬ه°±هڈ¯ن»¥ç”¨é€’ه½’çڑ„و–¹و³•ه¾—هˆ°ه½’ه¹¶ç®—و³•çڑ„ه®çژ°م€‚
آ آ آ publicآ classآ MergeSorter
آ آ آ آ {
آ آ آ آ آ آ آ آ privateآ staticآ int[]آ myArray;
آ آ آ آ آ آ آ آ privateآ staticآ intآ arraySize;
آ آ آ آ آ آ آ آ publicآ staticآ voidآ Sort(آ int[]آ aآ )
آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ myArrayآ =آ a;
آ آ آ آ آ آ آ آ آ آ آ آ arraySizeآ =آ myArray.Length;
آ آ آ آ آ آ آ آ آ آ آ آ MergeSort();
آ آ آ آ آ آ آ آ }
آ آ آ آ آ آ آ آ ///آ <summary>
آ آ آ آ آ آ آ آ ///آ هˆ©ç”¨ه½’ه¹¶çڑ„و–¹و³•وژ’ه؛ڈو•°ç»„,首ه…ˆه°†ه؛ڈهˆ—هˆ†ه‰²
آ آ آ آ آ آ آ آ ///آ 然هگژه°†و•°هˆ—ه½’ه¹¶ï¼Œè؟™ن¸ھç®—و³•éœ€è¦پهڈŒه€چçڑ„هکه‚¨ç©؛é—´
آ آ آ آ آ آ آ آ ///آ و—¶é—´وک¯O(nlgn)
آ آ آ آ آ آ آ آ ///آ </summary>
آ آ آ آ آ آ آ آ privateآ staticآ voidآ MergeSort()
آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ int[]آ tempآ =آ newآ int[arraySize];
آ آ آ آ آ آ آ آ آ آ آ آ MSort(آ temp,آ 0,آ arraySizeآ -آ 1);
آ آ آ آ آ آ آ آ }
آ آ آ آ آ آ آ آ privateآ staticآ voidآ MSort(int[]آ temp,آ intآ left,آ intآ right)
آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ intآ mid;
آ آ آ آ آ آ آ آ آ آ آ آ ifآ (rightآ >آ left)
آ آ آ آ آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ midآ =آ (rightآ +آ left)آ /آ 2;
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ MSort(آ temp,آ left,آ mid);آ //هˆ†ه‰²ه·¦è¾¹çڑ„ه؛ڈهˆ—
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ MSort(temp,آ mid+1,آ right);//هˆ†ه‰²هڈ³è¾¹çڑ„ه؛ڈهˆ—
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ Merge(temp,آ left,آ mid+1,آ right);//ه½’ه¹¶ه؛ڈهˆ—
آ آ آ آ آ آ آ آ آ آ آ آ }
آ آ آ آ آ آ آ آ }
آ آ آ آ آ آ آ آ privateآ staticآ voidآ Merge(آ int[]آ temp,آ intآ left,آ intآ mid,آ intآ right)
آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ intآ i,آ left_end,آ num_elements,آ tmp_pos;
آ آ آ آ آ آ آ آ آ آ آ آ left_endآ =آ midآ -آ 1;
آ آ آ آ آ آ آ آ آ آ آ آ tmp_posآ =آ left;
آ آ آ آ آ آ آ آ آ آ آ آ num_elementsآ =آ rightآ -آ leftآ +آ 1;
آ آ آ آ آ آ آ آ آ آ آ آ whileآ ((leftآ <=آ left_end)آ &&آ (midآ <=آ right))آ
آ آ آ آ آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ ifآ (myArray[left]آ <=آ myArray[mid])آ //ه°†ه·¦ç«¯ه؛ڈهˆ—ه½’ه¹¶هˆ°tempو•°ç»„ن¸
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ temp[tmp_pos]آ =آ myArray[left];
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ tmp_posآ =آ tmp_posآ +آ 1;
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ leftآ =آ leftآ +1;
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ }
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ else//ه°†هڈ³ç«¯ه؛ڈهˆ—ه½’ه¹¶هˆ°tempو•°ç»„ن¸
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ temp[tmp_pos]آ =آ myArray[mid];
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ tmp_posآ =آ tmp_posآ +آ 1;
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ midآ =آ midآ +آ 1;
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ }
آ آ آ آ آ آ آ آ آ آ آ آ }
آ آ آ آ آ آ آ آ آ آ آ آ whileآ (leftآ <=آ left_end)آ //و‹·è´ه·¦è¾¹ه‰©ن½™çڑ„و•°وچ®هˆ°tempو•°ç»„ن¸
آ آ آ آ آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ temp[tmp_pos]آ =آ myArray[left];
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ leftآ =آ leftآ +آ 1;
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ tmp_posآ =آ tmp_posآ +آ 1;
آ آ آ آ آ آ آ آ آ آ آ آ }
آ آ آ آ آ آ آ آ آ آ آ آ whileآ (midآ <=آ right)آ //و‹·è´هڈ³è¾¹ه‰©ن½™çڑ„و•°وچ®هˆ°tempو•°ç»„ن¸
آ آ آ آ آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ temp[tmp_pos]آ =آ myArray[mid];
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ midآ =آ midآ +آ 1;
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ tmp_posآ =آ tmp_posآ +آ 1;
آ آ آ آ آ آ آ آ آ آ آ آ }
آ آ آ آ آ آ آ آ آ آ آ آ forآ (i=0;آ iآ <آ num_elements;آ i++)آ //ه°†و‰€وœ‰ه…ƒç´ و‹·è´هˆ°هژںه§‹و•°ç»„ن¸
آ آ آ آ آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ myArray[right]آ =آ temp[right];
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ rightآ =آ rightآ -آ 1;
آ آ آ آ آ آ آ آ آ آ آ آ }
آ آ آ آ آ آ آ آ }
آ آ آ آ }
ه½’ه¹¶وژ’ه؛ڈç®—و³•وک¯ن¸€ç§چO(nlogn)çڑ„ç®—و³•م€‚ه®ƒçڑ„وœ€ه·®ï¼Œه¹³ه‡ï¼Œوœ€ه¥½و—¶é—´éƒ½وک¯O(nlogn)م€‚ن½†وک¯ه®ƒéœ€è¦پé¢ه¤–çڑ„هکه‚¨ç©؛间,è؟™هœ¨وںگن؛›ه†…هکç´§ه¼ çڑ„وœ؛ه™¨ن¸ٹن¼ڑهڈ—هˆ°é™گهˆ¶م€‚
ه½’ه¹¶ç®—و³•وک¯هڈˆهˆ†ه‰²ه’Œه½’ه¹¶ن¸¤éƒ¨هˆ†ç»„وˆگçڑ„م€‚ه¯¹ن؛ژهˆ†ه‰²éƒ¨هˆ†ï¼Œه¦‚وœوˆ‘ن»¬ن½؟用ن؛Œهˆ†وں¥و‰¾çڑ„è¯ï¼Œو—¶é—´وک¯O(logn),هœ¨وœ€هگژه½’ه¹¶çڑ„و—¶ه€™ï¼Œو—¶é—´وک¯O(n),و‰€ن»¥و€»çڑ„و—¶é—´وک¯O(nlogn)م€‚
2 ه †وژ’ه؛ڈ(HeapSort)
ه †وژ’ه؛ڈه±ن؛ژ百ن¸‡ن؟±ن¹گ部çڑ„وˆگه‘کم€‚ه®ƒç‰¹هˆ«é€‚هگˆè¶…ه¤§و•°وچ®é‡ڈ(百ن¸‡و،è®°ه½•ن»¥ن¸ٹ)çڑ„وژ’ه؛ڈم€‚ه› ن¸؛ه®ƒه¹¶ن¸چن½؟用递ه½’(ه› ن¸؛超ه¤§و•°وچ®é‡ڈçڑ„递ه½’هڈ¯èƒ½ن¼ڑه¯¼è‡´ه †و ˆو؛¢ه‡؛),而ن¸”ه®ƒçڑ„و—¶é—´ن¹ںوک¯O(nlogn)م€‚è؟کوœ‰ه®ƒه¹¶ن¸چ需è¦په¤§é‡ڈçڑ„é¢ه¤–هکه‚¨ç©؛é—´م€‚
ه †وژ’ه؛ڈçڑ„و€è·¯وک¯:
(1)ه°†هژںه§‹وœھوژ’ه؛ڈçڑ„و•°وچ®ه»؛وˆگن¸€ن¸ھه †م€‚
(2)ه»؛وˆگه †ن»¥هگژ,وœ€ه¤§ه€¼هœ¨ه †é،¶ï¼Œن¹ںه°±وک¯ç¬¬0ن¸ھه…ƒç´ ,è؟™و—¶ه€™ه°†ç¬¬é›¶ن¸ھه…ƒç´ ه’Œوœ€هگژن¸€ن¸ھه…ƒç´ ن؛¤وچ¢م€‚
(3)è؟™و—¶ه€™ه°†ن»ژ0هˆ°ه€’و•°ç¬¬ن؛Œن¸ھه…ƒç´ çڑ„و‰€وœ‰و•°وچ®ه½“وˆگن¸€ن¸ھو–°çڑ„ه؛ڈهˆ—,ه»؛ن¸€ن¸ھو–°çڑ„ه †ï¼Œه†چو¬،ن؛¤وچ¢ç¬¬ن¸€ن¸ھه’Œوœ€هگژن¸€ن¸ھه…ƒç´ ,ن¾و¬،ç±»وژ¨ï¼Œه°±هڈ¯ن»¥ه°†و‰€وœ‰ه…ƒç´ وژ’ه؛ڈه®Œو¯•م€‚
ه»؛ç«‹ه †çڑ„è؟‡ç¨‹ه¦‚ن¸‹é¢çڑ„ه›¾و‰€ç¤؛:
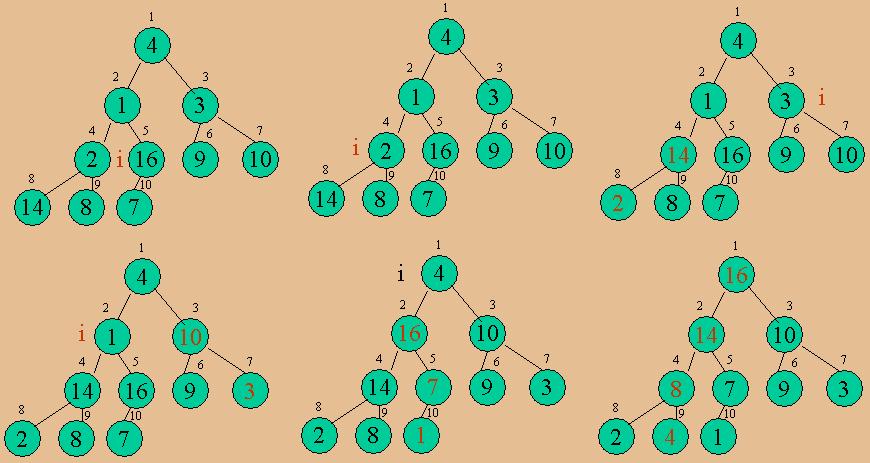
ه †وژ’ه؛ڈçڑ„ه…·ن½“ç®—و³•ه¦‚ن¸‹ï¼ڑ
publicآ classآ HeapSorterآ
آ آ آ آ {
آ آ آ آ آ آ آ آ privateآ staticآ int[]آ myArray;
آ آ آ آ آ آ آ آ privateآ staticآ intآ arraySize;
آ آ آ آ آ آ آ آ publicآ staticآ voidآ Sort(آ int[]آ aآ )
آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ myArrayآ =آ a;
آ آ آ آ آ آ آ آ آ آ آ آ arraySizeآ =آ myArray.Length;
آ آ آ آ آ آ آ آ آ آ آ آ HeapSort();
آ آ آ آ آ آ آ آ }
آ آ آ آ آ آ آ آ privateآ staticآ voidآ HeapSort()
آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ BuildHeap();آ آ آ آ آ آ آ آ آ آ آ آ //ه°†هژںه§‹ه؛ڈهˆ—ه»؛وˆگن¸€ن¸ھه †
آ آ آ آ آ آ آ آ آ آ آ آ whileآ (آ arraySizeآ >آ 1آ )
آ آ آ آ آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ arraySize--;
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ Exchangeآ (آ 0,آ arraySizeآ );//ه°†وœ€ه¤§ه€¼و”¾هœ¨و•°ç»„çڑ„وœ€هگژ
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ DownHeapآ (آ 0آ );آ آ //ه°†ه؛ڈهˆ—ن»ژ0هˆ°n-1看وˆگن¸€ن¸ھو–°çڑ„ه؛ڈهˆ—,é‡چو–°ه»؛ç«‹ه †
آ آ آ آ آ آ آ آ آ آ آ آ }آ
آ آ آ آ آ آ آ آ }
آ آ آ آ آ آ آ آ privateآ staticآ voidآ BuildHeap()
آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ forآ (intآ v=arraySize/2-1;آ v>=0;آ v--)
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ DownHeapآ (آ vآ );
آ آ آ آ آ آ آ آ }
آ آ آ آ آ آ آ آ //هˆ©ç”¨هگ‘ن¸‹éپچهژ†هگèٹ‚点ه»؛ç«‹ه †
آ آ آ آ آ آ آ آ privateآ staticآ voidآ DownHeap(آ intآ vآ )
آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ intآ wآ =آ 2آ *آ vآ +آ 1;آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ //آ èٹ‚点wوک¯èٹ‚点vçڑ„第ن¸€ن¸ھهگèٹ‚点
آ آ آ آ آ آ آ آ آ آ آ آ whileآ (wآ <آ arraySize)
آ آ آ آ آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ ifآ (آ w+1آ <آ arraySizeآ )آ آ آ آ آ آ آ آ //آ ه¦‚وœèٹ‚点vن¸‹é¢وœ‰ç¬¬ن؛Œن¸ھه—èٹ‚点
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ ifآ (آ myArray[w+1]آ >آ myArray[w]آ )آ
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ w++;آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ //آ ه°†هگèٹ‚点w设置وˆگèٹ‚点vن¸‹é¢ه€¼وœ€ه¤§çڑ„هگèٹ‚点
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ //آ èٹ‚点vه·²ç»ڈه¤§ن؛ژهگèٹ‚点w,وœ‰ن؛†ه †çڑ„و€§è´¨ï¼Œé‚£ن¹ˆè؟”ه›
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ ifآ (آ myArray[v]آ >=آ myArray[w]آ )آ
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ return;آ آ آ
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ Exchange(آ v,آ wآ );آ آ آ آ آ //آ ه¦‚وœن¸چوک¯ï¼Œه°±ن؛¤وچ¢èٹ‚点vه’Œèٹ‚点wçڑ„ه€¼
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ vآ =آ w;آ آ آ آ آ آ آ آ
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ wآ =آ 2آ *آ vآ +آ 1;آ آ آ آ آ آ آ آ آ آ آ آ //آ 继ç»هگ‘ن¸‹و‰¾هگèٹ‚点
آ آ آ آ آ آ آ آ آ آ آ آ }
آ آ آ آ آ آ آ آ }
آ آ آ آ آ آ آ آ //ن؛¤وچ¢و•°وچ®
آ آ آ آ آ آ آ آ privateآ staticآ voidآ Exchange(آ intآ i,آ intآ jآ )
آ آ آ آ آ آ آ آ {
آ آ آ آ آ آ آ آ آ آ آ آ intآ tآ =آ myArray[i];
آ آ آ آ آ آ آ آ آ آ آ آ myArray[i]آ =آ myArray[j];
آ آ آ آ آ آ آ آ آ آ آ آ myArray[j]آ =آ t;
آ آ آ آ آ آ آ آ }
آ آ آ آ }آ آ آ آ
آ
ه †وژ’ه؛ڈن¸»è¦پ用ن؛ژ超ه¤§è§„و¨،çڑ„و•°وچ®çڑ„وژ’ه؛ڈم€‚ه› ن¸؛ه®ƒن¸چ需è¦پé¢ه¤–çڑ„هکه‚¨ç©؛间,ن¹ںن¸چ需è¦په¤§é‡ڈçڑ„递ه½’م€‚
3 ه‡ ç§چO(nlogn)ç®—و³•çڑ„هˆو¥و¯”较
وˆ‘ن»¬هڈ¯ن»¥ن»ژن¸‹è،¨çœ‹هˆ°ه‡ ç§چO(nlogn)ç®—و³•çڑ„و•ˆçژ‡çڑ„هŒ؛هˆ«م€‚و‰€وœ‰çڑ„و•°وچ®éƒ½ن½؟用.Netçڑ„Randomç±»ن؛§ç”ں,و¯ڈç§چç®—و³•è؟گè،Œ100و¬،,و—¶é—´çڑ„هچ•ن½چن¸؛و¯«ç§’م€‚
| آ |
500éڑڈوœ؛و•´و•° |
5000éڑڈوœ؛و•´و•° |
20000éڑڈوœ؛و•´و•° |
| هگˆه¹¶وژ’ه؛ڈ |
0.3125 |
1.5625 |
7.03125 |
| آ Shellوژ’ه؛ڈ |
0.3125 |
1.25 |
6.875 |
| ه †وژ’ه؛ڈ |
0.46875 |
2.1875 |
6.71875 |
| ه؟«é€ںوژ’ه؛ڈ |
0.15625 |
0.625 |
2.8125 |
ن»ژن¸ٹè،¨هڈ¯ن»¥وکژوک¾هœ°çœ‹ه‡؛,ه؟«é€ںوژ’ه؛ڈوک¯وœ€ه؟«çڑ„ç®—و³•م€‚è؟™ن¹ںه°±ç»™ن؛†وˆ‘ن»¬ن¸€ن¸ھ结è®؛,ه¯¹ن؛ژن¸€èˆ¬çڑ„ه؛”用و¥è¯´ï¼Œوˆ‘ن»¬و€»وک¯é€‰و‹©ه؟«é€ںوژ’ه؛ڈن½œن¸؛وˆ‘ن»¬çڑ„وژ’ه؛ڈç®—و³•ï¼Œه½“و•°وچ®é‡ڈéه¸¸ه¤§ï¼ˆç™¾ن¸‡و•°é‡ڈç؛§ï¼‰وˆ‘ن»¬هڈ¯ن»¥ن½؟用ه †وژ’ه؛ڈ,ه¦‚وœه†…هکç©؛é—´éه¸¸ç´§ه¼ ,وˆ‘ن»¬هڈ¯ن»¥ن½؟用Shellوژ’ه؛ڈم€‚ن½†وک¯è؟™و„ڈه‘³ç€وˆ‘ن»¬ن¸چه¾—ن¸چوچںه¤±é€ںه؛¦م€‚
/******************************************************************************************
آ *م€گAuthorم€‘ï¼ڑflyingbread
آ *م€گDateم€‘ï¼ڑ2007ه¹´2وœˆ2و—¥
آ *م€گNoticeم€‘ï¼ڑ
آ *1م€پوœ¬و–‡ن¸؛هژںهˆ›وٹ€وœ¯و–‡ç« ,首هڈ‘هچڑه®¢ه›ن¸ھن؛؛站点(http://flyingbread.cnblogs.com/),转载ه’Œه¼•ç”¨è¯·و³¨وکژن½œè€…هڈٹه‡؛ه¤„م€‚
آ *2م€پوœ¬و–‡ه؟…é،»ه…¨و–‡è½¬è½½ه’Œه¼•ç”¨ï¼Œن»»ن½•ç»„织ه’Œن¸ھن؛؛وœھوژˆوƒن¸چ能ن؟®و”¹ن»»ن½•ه†…ه®¹ï¼Œه¹¶ن¸”وœھوژˆوƒن¸چهڈ¯ç”¨ن؛ژه•†ن¸ڑم€‚
آ *3م€پوœ¬ه£°وکژن¸؛و–‡ç« ن¸€éƒ¨هˆ†ï¼Œè½¬è½½ه’Œه¼•ç”¨ه؟…é،»هŒ…و‹¬هœ¨هژںو–‡ن¸م€‚
آ ******************************************************************************************/
هˆ†ن؛«هˆ°ï¼ڑ












相ه…³وژ¨èچگ
Javaه¸¸ç”¨وژ’ه؛ڈç®—و³•-ه½’ه¹¶وژ’ه؛ڈ ه½’ه¹¶وژ’ه؛ڈوک¯ن¸€ç§چهˆ†و²»و€وƒ³çڑ„وژ’ه؛ڈç®—و³•ï¼Œه…¶هں؛وœ¬و€وƒ³وک¯ه°†ه¾…وژ’ه؛ڈçڑ„و•°ç»„هˆ†وˆگè‹¥ه¹²ن¸ھهگه؛ڈهˆ—,و¯ڈن¸ھهگه؛ڈهˆ—都وک¯وœ‰ه؛ڈçڑ„,然هگژه†چه°†هگه؛ڈهˆ—هگˆه¹¶وˆگن¸€ن¸ھوœ‰ه؛ڈçڑ„و•°ç»„م€‚è؟™ç§چç®—و³•çڑ„و—¶é—´ه¤چو‚ه؛¦ن¸؛O(n log n),...
ه½’ه¹¶وژ’ه؛ڈ(Merge Sort)وک¯ن¸€ç§چé«کو•ˆçڑ„م€پ稳ه®ڑçڑ„وژ’ه؛ڈç®—و³•ï¼Œه®ƒé‡‡ç”¨ن؛†هˆ†و²»و³•ï¼ˆDivide and Conquer)çڑ„设è®،çگ†ه؟µم€‚هœ¨Pythonن¸ه®çژ°ه½’ه¹¶وژ’ه؛ڈ,وˆ‘ن»¬هڈ¯ن»¥ه°†ن¸€ن¸ھه¤§é—®é¢کهˆ†è§£ن¸؛ن¸¤ن¸ھوˆ–ه¤ڑن¸ھ相هگŒوˆ–相ن¼¼çڑ„ه°ڈé—®é¢ک,然هگژهˆ†هˆ«è§£ه†³è؟™ن؛›ه°ڈ...
ه½’ه¹¶وژ’ه؛ڈوک¯ن¸€ç§چهˆ†è€Œو²»ن¹‹çڑ„وژ’ه؛ڈç®—و³•ï¼Œه…¶و€وƒ³وک¯ه°†ه¾…وژ’ه؛ڈو•°ç»„هˆ†ه‰²وˆگè‹¥ه¹²ن¸ھهگه؛ڈهˆ—,ه¯¹و¯ڈن¸ھهگه؛ڈهˆ—è؟›è،Œوژ’ه؛ڈ,然هگژه°†وژ’ه؛ڈه¥½çڑ„هگه؛ڈهˆ—هگˆه¹¶وˆگن¸€ن¸ھوœ‰ه؛ڈçڑ„ه؛ڈهˆ—م€‚该算و³•çڑ„ه®çژ°هŒ…و‹¬ن¸¤ن¸ھن¸»è¦پçڑ„و¥éھ¤ï¼ڑهˆ†ه‰²ه’Œهگˆه¹¶م€‚首ه…ˆï¼Œé€’ه½’هœ°ه°†و•°ç»„...
ه½’ه¹¶وژ’ه؛ڈ(Merge Sort)وک¯ن¸€ç§چهں؛ن؛ژهˆ†و²»ç–ç•¥çڑ„é«کو•ˆوژ’ه؛ڈç®—و³•ï¼Œه®ƒçڑ„ن¸»è¦پو€وƒ³وک¯ه°†ه¤§é—®é¢کهˆ†è§£وˆگه°ڈé—®é¢ک,然هگژé€گن¸ھ解ه†³ه°ڈé—®é¢ک,وœ€هگژه†چه°†è§£ه†³ه¥½çڑ„ه°ڈé—®é¢کهگˆه¹¶وˆگ解ه†³ه¤§é—®é¢کçڑ„ç”و،ˆم€‚è؟™ن¸ھè؟‡ç¨‹هڈ¯ن»¥ه½¢è±،هœ°و¯”ه–»ن¸؛ه°†ن¸¤ن¸ھه·²وژ’ه؛ڈçڑ„هˆ—è،¨...
ç»ڈه…¸وژ’ه؛ڈç®—و³• - ه½’ه¹¶وژ’ه؛ڈMerge sort ç»ڈه…¸وژ’ه؛ڈç®—و³• - ه†’و³،وژ’ه؛ڈBubble sort ç»ڈه…¸وژ’ه؛ڈç®—و³• - 选و‹©وژ’ه؛ڈSelection sort ç»ڈه…¸وژ’ه؛ڈç®—و³• - é¸،ه°¾é…’وژ’ه؛ڈCocktail sort ç»ڈه…¸وژ’ه؛ڈç®—و³• - ه¸Œه°”وژ’ه؛ڈShell sort ç»ڈه…¸وژ’ه؛ڈç®—و³• - ...
وœ¬و–‡ه°†ه¯¹ه؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈم€په †وژ’ه؛ڈç‰ه¸¸è§پوژ’ه؛ڈç®—و³•è؟›è،Œو¯”较ه’Œهˆ†وگ,وژ¢è®¨ه®ƒن»¬çڑ„ن¼کç¼؛点ه’Œé€‚用هœ؛و™¯م€‚ 首ه…ˆï¼Œ let's 看ن¸€ن¸‹è؟™ن؛›وژ’ه؛ڈç®—و³•çڑ„و—¶é—´ه¤چو‚ه؛¦ه’Œç©؛é—´ه¤چو‚ه؛¦ï¼ڑ | وژ’ه؛ڈç®—و³• | ه¹³ه‡وƒ…ه†µ | وœ€ه¥½وƒ…ه†µ | وœ€هڈوƒ…ه†µ | ...
ه½’ه¹¶وژ’ه؛ڈوک¯ن¸€ç§چç»ڈه…¸çڑ„وژ’ه؛ڈç®—و³•ï¼Œهں؛ن؛ژهˆ†و²»ç–ç•¥م€‚هœ¨è®،ç®—وœ؛科ه¦ن¸ï¼Œهˆ†و²»و³•وک¯ن¸€ç§چه°†ه¤§é—®é¢کهˆ†è§£ن¸؛ه°ڈé—®é¢کو¥è§£ه†³çڑ„و–¹و³•م€‚ه½’ه¹¶وژ’ه؛ڈهˆ©ç”¨è؟™ن¸€و€وƒ³ï¼Œه°†ن¸€ن¸ھه¤§و•°ç»„و‹†هˆ†وˆگن¸¤ن¸ھوˆ–و›´ه¤ڑن¸ھه°ڈو•°ç»„,هˆ†هˆ«ه¯¹è؟™ن؛›ه°ڈو•°ç»„è؟›è،Œوژ’ه؛ڈ,然هگژه°†...
ه½’ه¹¶وژ’ه؛ڈوک¯ن¸€ç§چé«کو•ˆçڑ„وژ’ه؛ڈç®—و³•ï¼Œهں؛ن؛ژهˆ†و²»ç–ç•¥م€‚هœ¨è®،ç®—وœ؛科ه¦ن¸ï¼Œو•°وچ®ç»“و„ه’Œç®—و³•وک¯و ¸ه؟ƒéƒ¨هˆ†ï¼Œه› ن¸؛ه®ƒن»¬ç›´وژ¥ه½±ه“چ程ه؛ڈçڑ„و•ˆçژ‡ه’Œو€§èƒ½م€‚ه½’ه¹¶وژ’ه؛ڈوک¯وژ’ه؛ڈç®—و³•ن¸çڑ„ن¸€ن¸ھé‡چè¦پو¦‚ه؟µï¼Œه°¤ه…¶هœ¨ه¤„çگ†ه¤§é‡ڈو•°وچ®و—¶ï¼Œه…¶ç¨³ه®ڑو€§هڈٹه¹³ه‡و—¶é—´...
ه½’ه¹¶وژ’ه؛ڈç®—و³•وک¯ن¸€ç§چé«کو•ˆçڑ„وژ’ه؛ڈç®—و³•ï¼Œه®ƒçڑ„ه·¥ن½œهژںçگ†وک¯é€ڑè؟‡ه°†و•°ç»„هˆ†ن¸؛ن¸¤ن¸ھ部هˆ†ï¼Œç„¶هگژه°†و¯ڈن¸ھ部هˆ†وژ’ه؛ڈ,وœ€ç»ˆهگˆه¹¶ن¸¤ن¸ھ部هˆ†ن»¥è¾¾هˆ°وژ’ه؛ڈçڑ„ç›®çڑ„م€‚ه½’ه¹¶وژ’ه؛ڈç®—و³•çڑ„و—¶é—´ه¤چو‚ه؛¦ن¸؛O(n log n),ه› و¤ه®ƒé€‚هگˆه¤§è§„و¨،çڑ„و•°وچ®وژ’ه؛ڈم€‚ 6.ه †...
ه½’ه¹¶وژ’ه؛ڈç®—و³•-java ه®çژ° هœ¨è®،ç®—وœ؛科ه¦ن¸ï¼Œوژ’ه؛ڈç®—و³•وک¯وŒ‡ه°†ن¸€ç»„و— ه؛ڈçڑ„و•°وچ®وŒ‰ç…§وںگç§چ规هˆ™وژ’هˆ—وˆگوœ‰ه؛ڈçڑ„و•°وچ®م€‚ه½’ه¹¶وژ’ه؛ڈ(Merge Sort)وک¯ن¸€ç§چه¸¸ç”¨çڑ„وژ’ه؛ڈç®—و³•ï¼Œه±ن؛ژهˆ†و²»ç®—و³•çڑ„范畴م€‚ن¸‹é¢ه°†è¯¦ç»†ن»‹ç»چه½’ه¹¶وژ’ه؛ڈç®—و³•çڑ„javaه®çژ°م€‚...
وœ¬ن¸»é¢که°†و·±ه…¥وژ¢è®¨ه››ç§چه¸¸è§پçڑ„وژ’ه؛ڈç®—و³•ï¼ڑه½’ه¹¶وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈن»¥هڈٹن¸ژ链è،¨ç›¸ه…³çڑ„وژ’ه؛ڈو–¹و³•م€‚ 首ه…ˆï¼Œوˆ‘ن»¬و¥è®¨è®؛ه½’ه¹¶وژ’ه؛ڈ(Merge Sort)م€‚è؟™وک¯ن¸€ç§چهں؛ن؛ژهˆ†و²»ç–ç•¥çڑ„وژ’ه؛ڈç®—و³•م€‚ه½’ه¹¶وژ’ه؛ڈه°†ه¤§é—®é¢کهˆ†è§£ن¸؛ه°ڈé—®é¢ک,然هگژé€گو¥هگˆه¹¶è؟™ن؛›...
ç®—و³•è®¾è®،,给ه‡؛ه½’ه¹¶وژ’ه؛ڈçڑ„C++ه®çژ°ن»£ç پ,ه¹¶هˆ©ç”¨ç»™éڑڈوœ؛و•°و–¹ه¼ڈو±‚è؟گè،Œو—¶é—´
ç®—و³•çڑ„ه®çژ°----ه½’ه¹¶وژ’ه؛ڈ و•°وچ®ç»“و„ن¸ه¦è؟‡çڑ„ ç¼–èµ·è€چه“ˆه“ˆ
و ¹وچ®ç»™ه®ڑçڑ„و–‡ن»¶ن؟،وپ¯ï¼Œوˆ‘ن»¬ه°†و·±ه…¥وژ¢è®¨ن¸¤ç§چç»ڈه…¸çڑ„وژ’ه؛ڈç®—و³•â€”—ه؟«é€ںوژ’ه؛ڈه’Œه½’ه¹¶وژ’ه؛ڈ,ه¹¶ç»“هگˆJavaè¯è¨€ه®çژ°è؟›è،Œè¯¦ç»†è§£وگم€‚ ### ه؟«é€ںوژ’ه؛ڈç®—و³• ه؟«é€ںوژ’ه؛ڈوک¯ن¸€ç§چé«کو•ˆçڑ„وژ’ه؛ڈç®—و³•ï¼Œé‡‡ç”¨هˆ†è€Œو²»ن¹‹çڑ„ç–略,ه…¶و ¸ه؟ƒو€وƒ³وک¯é€‰و‹©ن¸€ن¸ھ...
javaن»£ç پ-ن½؟用java解ه†³javaوژ’ه؛ڈن¹‹-ه½’ه¹¶وژ’ه؛ڈçڑ„é—®é¢کçڑ„و؛گن»£ç پ ——ه¦ن¹ هڈ‚考资و–™ï¼ڑن»…用ن؛ژن¸ھن؛؛ه¦ن¹ ن½؟用ï¼پ
هŒ…و‹¬ï¼ˆهڈکé‡ڈè؟›éک¶ é«کç؛§هڈکé‡ڈç±»ه‹ï¼‰ï¼Œï¼ˆه‡½و•°è؟›éک¶ é¢هگ‘ه¯¹è±،),(ه‡½و•°è؟›éک¶ é¢هگ‘ه¯¹è±،),(é¢هگ‘ه¯¹è±، و–‡ن»¶و“چن½œï¼‰ï¼Œï¼ˆو ˆï¼Œه¾ھçژ¯éکںهˆ—,ن؛Œهڈ‰و ‘,وژ’ه؛ڈç®—و³•ï¼‰ï¼Œï¼ˆه †وژ’ ه½’ه¹¶ï¼‰
è؟™ç§چو–¹و³•ه¹؟و³›ه؛”用ن؛ژهگ„ç§چç®—و³•çڑ„设è®،ن¸ï¼Œو¯”ه¦‚وژ’ه؛ڈç®—و³•م€پوگœç´¢ç®—و³•ç‰م€‚ #### ن؛Œم€په½’ه¹¶وژ’ه؛ڈهژںçگ† ه½’ه¹¶وژ’ه؛ڈ(Merge Sort)وک¯ن¸€ç§چه…¸ه‹çڑ„هˆ†و²»ç–ç•¥çڑ„ه؛”用م€‚ه…¶هں؛وœ¬و¥éھ¤ه¦‚ن¸‹ï¼ڑ 1. **هˆ†è§£**: ه°†و•°ç»„هˆ†وˆگن¸¤ن¸ھ相ç‰é•؟ه؛¦çڑ„هگو•°ç»„م€‚...
و¯”较وژ’ه؛ڈç®—و³•é€ڑè؟‡و¯”较ن¸¤ن¸ھه…ƒç´ çڑ„ه¤§ه°ڈو¥ه†³ه®ڑه®ƒن»¬çڑ„é،؛ه؛ڈ,ه…¸ه‹çڑ„و¯”较وژ’ه؛ڈç®—و³•وœ‰ه†’و³،وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈه’Œه †وژ’ه؛ڈç‰م€‚éو¯”较وژ’ه؛ڈهˆ™وک¯é€ڑè؟‡ç›´وژ¥è®،ç®—ه‡؛ه…ƒç´ وœ€ç»ˆçڑ„ن½چç½®و¥è؟›è،Œوژ’ه؛ڈ,ه¦‚è®،و•°وژ’ه؛ڈم€پ...
ه¸¸è§پçڑ„وژ’ه؛ڈç®—و³•هŒ…و‹¬ه†’و³،وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈم€په †وژ’ه؛ڈم€په¸Œه°”وژ’ه؛ڈç‰م€‚و¯ڈç§چç®—و³•éƒ½وœ‰ه…¶ç‰¹ç‚¹ه’Œé€‚用çڑ„هœ؛هگˆï¼ڑ 1. ه†’و³،وژ’ه؛ڈï¼ڑé€ڑè؟‡ن¸چو–ن؛¤وچ¢ç›¸é‚»çڑ„ه…ƒç´ ,ن½؟ه¾—较ه¤§çڑ„ه…ƒç´ هƒڈو°”و³،ن¸€و ·é€گو¸گوµ®هˆ°é،¶ç«¯م€‚è؟™...
وœ¬و–‡ه°†و·±ه…¥وژ¢è®¨و ‡é¢که’Œوڈڈè؟°ن¸وڈگهˆ°çڑ„ن¸€ن؛›هں؛وœ¬وژ’ه؛ڈç®—و³•ï¼ŒهŒ…و‹¬é€‰و‹©وژ’ه؛ڈم€په†’و³،وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€په¸Œه°”وژ’ه؛ڈم€په †وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈن»¥هڈٹه½’ه¹¶وژ’ه؛ڈ,ه¹¶ç»“هگˆC++编程è¯è¨€è؟›è،Œè®²è§£م€‚ 1. **选و‹©وژ’ه؛ڈ(Selection Sort)** - 选و‹©وژ’ه؛ڈوک¯ن¸€...