最小生成树 Kruscal经典算法

　文章作者：ktyanny  文章来源：ktyanny  转载请注明，谢谢合作。  

　　话说ktyanny昨天逃了一天的课，恶补并查集知识，就是为了写出经典得不得了的Kruscal最小生成树。今天早上9点钟爬起来，继续看了下Kruscal算法，顿然茅塞顿开了，哈哈

 

1、生成树的概念

　　连通图G的一个子图如果是一棵包含G的所有顶点的树，则该子图称为G的生成树。

　　生成树是连通图的极小连通子图。所谓极小是指：若在树中任意增加一条边，则将出现一个回路；若去掉一条边，将会使之变成非连通图。 生成树各边的权值总和称为生成树的权。权最小的生成树称为最小生成树。

 

2、最小生成树的性质

　　用哲学的观点来说，每个事物都有自己特有的性质，那么图的最小生成树也是不例外的。按照生成树的定义，n 个顶点的连通网络的生成树有 n 个顶点、n-1 条边。

 

3、构造最小生成树，要解决以下两个问题：

　　1.尽可能选取权值小的边，但不能构成回路（也就是环）。

　　2.选取n-1条恰当的边以连接网的 n个顶点。

 

4、 最小生成树Kruscal算法：

　　用ktyanny的口头陈述为，Kruscal算法实质是非朴素的贪心策略。初始状态，图的每个节点单独作为一个集合，图的边就绪状态为非降序排列。然后一次遍历图中的所有边(u, v)，使用并查集的思想 （不懂并查集的 点击此处 并查集（不相交集合）
进行学习 ） ，  find_set(u) 如果不等于find_set(v)，也就是u和v不在同一个集合中，那么相当于判断了添加了边(u, v)不会照成环。好！接下来的工作就是把需要的信息保存起来（比如边的信息之类的），同时合并u和v（使用union_set(u, v)）.当所有的顶点都添加到集合中去了，好！算法完毕。

 

5、Kruscal算法举例演示 

　　假设部分：图中有9个顶点依次为a、b、c、d、e、f、g、h、i，各条边的权值直接看下面的图吧。

　　大概的过程看下面的步骤：下面给出的图很囧……（是因为我相机还不够高级，等挣钱了买个漂亮的），不过没关系，主要自己看的明白就好了。

　　看清楚了，箭头指向的是要处理的边，粗线边表示为被接纳的边了。

 

 

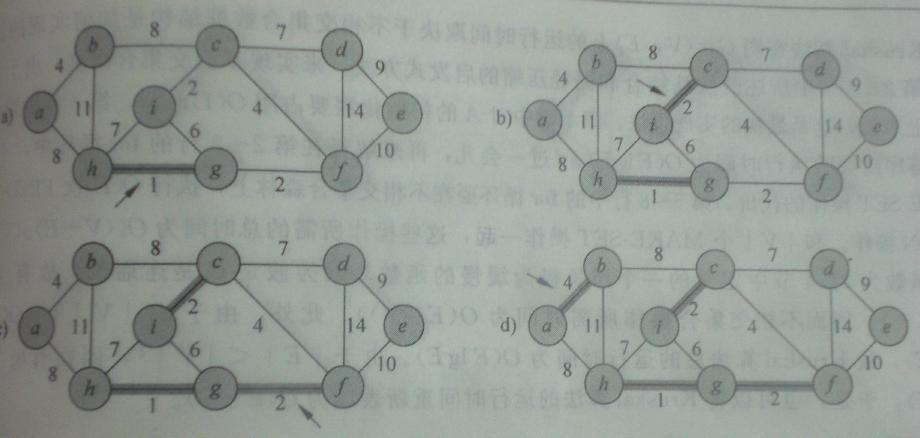
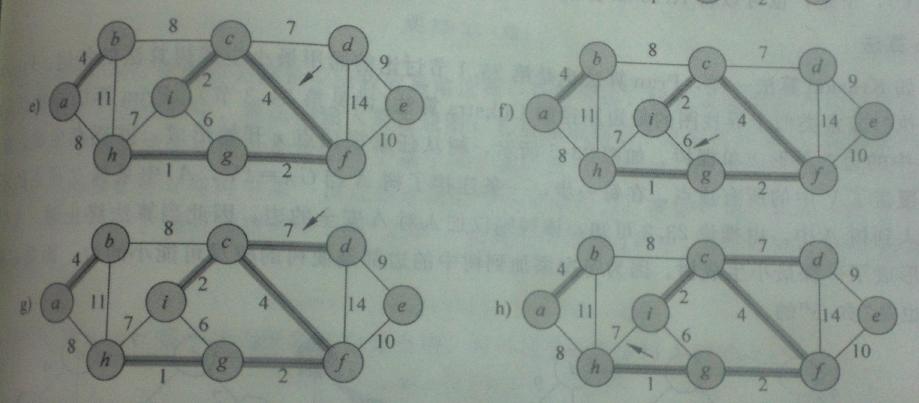
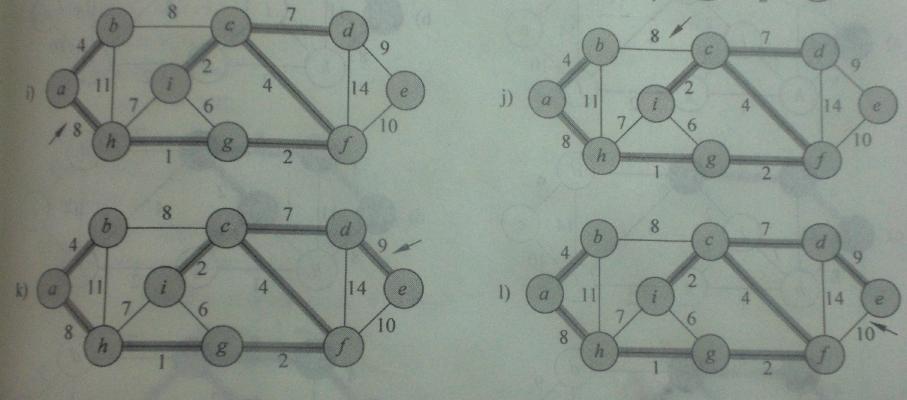
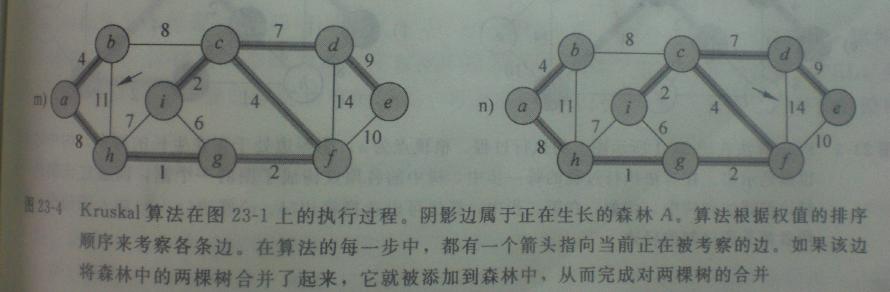
 　　好了，在这里还是要夸一下《算法导论》这本书。

 

6、核心部分的代码 

　　贴上比较好点的代码吧：

 

<!-- <br/ /><br/ />Code highlighting produced by Actipro CodeHighlighter (freeware)<br/ />http://www.CodeHighlighter.com/<br/ /><br/ />-->
const   int  MAX  =   100 ;  /* 图的顶点个数最大上限 */

typedef  struct
{
     int  x, y;
     int  w;
}edge;

edge e[MAX];

/* 上面描述为图的数据结构 */

/* 下面部分为主要部分，根据你的程序的需要惊醒添加吧 */     
         /* MST_Kruscal算法的实现过程 */
     /*  将边排序  */
    qsort(e, n,  sizeof (edge), cmp);
 
    sum  =   0 ;
 
     for  (i  =   0 ; i  <  n; i ++ )
    {
        x  =  find_set(e[i].x);
        y  =  find_set(e[i].y);  
         if  (x  !=  y)
        {
            union_set(x, y, e[i].w);
        }
    }
 

 

7、算法分析

 　　用Kruskal算法构造最小生成树的时间复杂度为O（eloge），与网中边的数目e有关，因此，它适用于求稀疏图的最小生成树。

　　我们还有一种思想比较复杂点的算法，prim算法，详情可以参考：最小生成树 普莱姆（prim）算法  

 

8、相关练习

HDU 1102 Constructing Roads （Kruscal最小生成树）

 

HDU 1162 Eddy's picture （Kruscal最小生成树）

 

HDU 1233 还是畅通工程 (Kruscal 最小生成树)

 

HDU 1301 Jungle Roads (Kruscal 最小生成树)  

 

HDU 1875 畅通工程再续（Kruscal最小生成树）