图像几何变换

DSQiu

浏览: 1407846 次
性别:
来自: 广州

最近访客更多访客>>

ymgjava

spike_wq

sdsunrunner

hackxboy

博主相关

博客

微博

相册

留言

关于我

博客专栏

: NGUI所见即所得
浏览量：196459

: Effective C# ...
浏览量：0

文章分类

社区版块

存档分类

博客分类：

数字图像处理

图像几何变换最邻近插值双线性插值三次卷积插值

一、放射变换

最为常用的几何变换都是线性变换，这包括旋转、缩放、切变、反射以及正投影。在二维空间中，线性变换可以用 2×2 的变换矩阵表示。

1.旋转变换

绕原点逆时针旋转 θ 度角的变换公式是 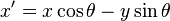$x' = x \cos \theta - y \sin \theta$ 与 $y' = x \sin \theta + y \cos \theta$ ，用矩阵表示为：

$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos \theta & - \sin\theta \\ \sin \theta & \cos \theta \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$

2.伸缩变换

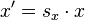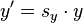缩放公式为 $x' = s_x \cdot x$ 与 $y' = s_y \cdot y$ ，用矩阵表示为：

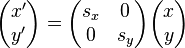
$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} s_x & 0 \\ 0 & s_y \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$

3.错切变换

错切变换公式： x = x0 + b*y0; y = d*x0 + y0; b,d分别是x,y平移的分量

用矩阵乘法表示变换为： Shear-Matrix

4.平移变换

矩阵乘法表示变换。 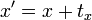$x' = x + t_x$ ; $y' = y + t_y$ 变为

$\begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$

二、图像插值放大

1.最邻近插值（近邻取样法）：
　　最临近插值的的思想很简单。对于通过反向变换得到的的一个浮点坐标，对其进行简单的取整，得到一个整数型坐标，这个整数型坐标对应的像素值就是目的像素的像素值，也就是说，取浮点坐标最邻近的左上角点对应的像素值。可见，最邻近插值简单且直观，但得到的图像质量不高。

2.双线性内插值：
　　对于一个目的像素，设置坐标通过反向变换得到的浮点坐标为(i+u,j+v)，其中i、j均为非负整数，u、v为[0,1)区间的浮点数，则这个像素得值 f(i+u,j+v) 可由原图像中坐标为 (i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所对应的周围四个像素的值决定，即：

　　　　f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1)

其中f(i,j)表示源图像(i,j)处的像素值，以此类推。
　　这就是双线性内插值法。双线性内插值法计算量大，但缩放后图像质量高，不会出现像素值不连续的的情况。由于双线性插值具有低通滤波器的性质，使高频分量受损，所以可能会使图像轮廓在一定程度上变得模糊。

3.三次卷积法
能够克服以上两种算法的不足，计算精度高，但计算亮大，他考虑一个浮点坐标(i+u,j+v)周围的16个邻点，目的像素值f(i+u,j+v)可由如下插值公式得到：

　　　　f(i+u,j+v) = [A] * [B] * [C]

[A]=[ S(u + 1)　S(u + 0)　S(u - 1)　S(u - 2) ]

　　┏ f(i-1, j-1)　f(i-1, j+0)　f(i-1, j+1)　f(i-1, j+2) ┓
[B]=┃ f(i+0, j-1)　f(i+0, j+0)　f(i+0, j+1)　f(i+0, j+2) ┃
　　┃ f(i+1, j-1)　f(i+1, j+0)　f(i+1, j+1)　f(i+1, j+2) ┃
　　┗ f(i+2, j-1)　f(i+2, j+0)　f(i+2, j+1)　f(i+2, j+2) ┛

　　┏ S(v + 1) ┓
[C]=┃ S(v + 0) ┃
　　┃ S(v - 1) ┃
　　┗ S(v - 2) ┛

　　 ┏ 1-2*Abs(x)^2+Abs(x)^3　　　　　 , 0<=Abs(x)<1
S(x)=｛ 4-8*Abs(x)+5*Abs(x)^2-Abs(x)^3　, 1<=Abs(x)<2 其中 S(x)是对 Sin(x*Pi)/x 的逼近（Pi是圆周率——π）
　　 ┗ 0　　　　　　　　　　　　　　　 , Abs(x)>=2

最邻近插值（近邻取样法）、双线性内插值、三次卷积法等插值算法对于旋转变换、错切变换、一般线性变换和非线性变换都适用。

三、编程实现

Java类库内置方法实现了图像几何变换有：旋转，缩放，错切和平移等变换，图像放大使用的算法是最临近插值方法，下面自己实现的算法进行实验，至于Java内置的方法通过调用Graphics2D相关函数设置参数就可以完成，可以查看相应文档。

1.旋转

	/****************************************************
	 * 图像旋转
	 * pix　 --原图像像素数组
	 * opix--输出图像像素数组 
	 * (x,y) --原图像坐标 0<=x<=w, 0<=y<=h
	 * (i,j) --输出图像坐标0<=i,j<=owh	 
	 * beta  --旋转角度
	 ****************************************************/
	public int[] imRotate(int[] pix, float beta, int iw, int ih, int owh)
	{
		//1.旋转后的新图像最大最小包围盒宽高
		int[] opix = new int[owh * owh];
		
		double t = beta / 180;    	     
       		
		float cos_beta =  (float)Math.cos(t * Math.PI);//顺时针旋转
		float sin_beta =  (float)Math.sin(t * Math.PI);
		
		//2.逆旋转变换, 计算输出图像点p(i,j)所对应的原图像的坐标(x,y)
		for(int i = 0;i < owh;i++)    
		{
			for(int j = 0;j < owh;j++)
			{				
				//旋转变换的逆变换
				float u = (j-owh/2)*cos_beta+(i-owh/2)*sin_beta;
				float v = (i-owh/2)*cos_beta-(j-owh/2)*sin_beta;
			
				//换成相对于原图像的绝对坐标
				u += iw/2;
				v += ih/2;
			
				int x = (int)u;
				int y = (int)v;

				int index = i * owh + j;
				//3.检验条件, 对满足条件的点(x,y),赋值F(i,j)=f(x,y)
				if((x >= 0) && (x <= iw - 1) && (y >= 0) && (y <= ih - 1))
					opix[index] = pix[y * iw + x];							
			}
		} 	 
	 	return opix;
	}

实验效果如下：

2.镜像变换

//镜象变换 	
    public int[] imMirror(int[] pixs, int w, int h, int n)
    {
    	int[] pix = new int[w * h];
    	    	   	
    	//根据镜象变换公式，计算(u,v)并赋值F(u,v)=f(i,j)
    	for(int j = 0; j < h; j++)
    	{
    		for(int i = 0; i < w; i++)
    		{
    			if(n == 0)     //水平
    			{	    			
	    			int u = w - 1 - i;
	    			int v = j;
	    			pix[v*w+u] = pixs[j*w+i]; 
    			}
    			else if(n == 1)//垂直
    			{	    			
	    			int u = i;
	    			int v = h - 1 - j;
	    			pix[v*w+u] = pixs[j*w+i]; 
    			}   			
    		}    		
    	}
    	return pix;
    }

实验效果如下：

3.错切变换

  * 错切变换算法
     * 1.计算图像四角点坐标
     * 2.计算包围图像的最小矩形，即包围盒的宽和高
     * 3.将处理包围盒内的所有像素设置为背景色
     * 4.根据错切变换公式，
     *   u = (int)(i + j * shx)
     *   v = (int)(i * shy + j)
     * 　计算(u,v)并赋值 F(u,v) = f(i,j)      
     **********************************************/
     
    public int[] imShear(int[] pixs, double shx, double shy, 
                         int w, int h, int ow, int oh)
    { 
        int[] pix = new int[ow * oh];
    	    	
    	//根据错切变换公式，计算(u,v)并赋值F(u,v)=f(i,j)
    	for(int j = 0; j < h; j++)
    	{
    		for(int i = 0; i < w; i++)
    		{
    			int u = (int)(i + j * shx);
    			int v = (int)(i * shy + j);
    			pix[v*ow+u] = pixs[j*w+i];    			
    		}    		
    	}
    	return pix;
    }

实验效果如下：

4.平移变换

  //平移变换算法
    public int[] imTrans(int[] pixs, int tx, int ty, 
                         int w, int h, int ow, int oh)
    { 
        int u, v;
        int[] pix = new int[ow * oh];
    	    	
    	//根据错切变换公式，计算(u,v)并赋值F(u,v)=f(i,j)
    	for(int j = 0; j < h; j++)
    	{
    		for(int i = 0; i < w; i++)
    		{
    			u = i + tx;
    			v = j + ty;
    			pix[v*ow+u] = pixs[j*w+i];    			
    		}    		
    	}
    	return pix;
    }

实验效果如下：

5.最邻近插值

 //最邻近插值
	public int[] nearNeighbor(int pixs[], int iw, int ih, 
	                          int ow, int oh, float p)
    {    	
        int opix[] = new int[ow * oh];//目标图像素数组
  	    
	    ColorModel cm = ColorModel.getRGBdefault();
	    for(int i = 0; i < oh; i++) 
	    {
	    	int u = (int)(i/p);
	    	for(int j = 0; j < ow; j++)
	    	{
	    		int r, g, b;    		
	    		int v = (int)(j/p);	            
	           
	            r = cm.getRed(pixs[u*iw+v]);
	            g = cm.getGreen(pixs[u*iw+v]);
	            b = cm.getBlue(pixs[u*iw+v]);
	            
	            opix[i*ow+j] = 255 << 24|r << 16|g << 8|b;
	        }
	    }
	    return opix;     
    }

实验效果如下：

6.双线性插值

 //双线性插值算法
    public int[] bilinear(int pixs[], int iw, int ih, int ow, int oh, float p)
    { 	
    	int pixd[]=new int[ow * oh];//目标图像素数组
  	    
	    ColorModel cm = ColorModel.getRGBdefault();
	    for(int i = 0; i < oh-1; i++) 
	    {
	    	float dy = i/p;
	    	int iy = (int)dy;
	    	if(iy > ih-2) iy = ih-2;
	    	float d_y = dy - iy;
	    	
	    	for(int j = 0; j < ow-1; j++) 
	    	{
	    		int a,r,g,b;
	    		float dx = j/p;    		
	    		int ix = (int)dx;
	    		if(ix > iw-2) ix = iw-2;
	    		float d_x= dx - ix;
	    		
	    		//f(i+u,j+v)=(1-u)(1-v)f(i,j)+u(1-v)f(i+1,j)+
	    		//           (1-u)vf(i,j+1)+uvf(i+1,j+1)
	    		r = (int)((1-d_x)*(1-d_y)*cm.getRed(pixs[iy*iw+ix])+
                          d_x*(1-d_y)*cm.getRed(pixs[iy*iw+ix+1])+
                          (1-d_x)*d_y*cm.getRed(pixs[(iy+1)*iw+ix])+
                          d_x*d_y*cm.getRed(pixs[(iy+1)*iw+ix+1]));
            	            
	            g = (int)((1-d_x)*(1-d_y)*cm.getGreen(pixs[iy*iw+ix])+
                          d_x*(1-d_y)*cm.getGreen(pixs[iy*iw+ix+1])+
                          (1-d_x)*d_y*cm.getGreen(pixs[(iy+1)*iw+ix])+
                          d_x*d_y*cm.getGreen(pixs[(iy+1)*iw+ix+1]));
            	            
	            b = (int)((1-d_x)*(1-d_y)*cm.getBlue(pixs[iy*iw+ix])+
                          d_x*(1-d_y)*cm.getBlue(pixs[iy*iw+ix+1])+
                          (1-d_x)*d_y*cm.getBlue(pixs[(iy+1)*iw+ix])+
                          d_x*d_y*cm.getBlue(pixs[(iy+1)*iw+ix+1]));
	            	            	            
	            pixd[i*ow+j] = 255 << 24|r << 16|g << 8|b;
	        }
	    }
	    return pixd;      
    }

实验效果如下：

7.三次卷积插值

  //对整个图像按给定的宽度和高度比例进行缩放
	public int[] scale(int[] pix, int iw, int ih, int ow, int oh, 
	                   float scalex, float scaley)
	{		
		int pixelsSrc[]  = new int[iw * ih];
		int pixelsDest[] = new int[ow * oh];
		
		//第三步,缩放图像
		this.scale(pix, 0, 0, iw, ih, iw, scalex, scaley, pixelsDest);
	 	return (pixelsDest);
	}
	
	/********************************************************
	 * src 原图像的像素数据,
	 * (x, y) 被缩放的区域在左上角的坐标,
	 * (w, h) 缩放区域的宽度和高度
	 * scansize 原图像的扫描宽度
	 * (scalex, scaley) 水平和垂直方向上的缩放比
	 * dst 缩放后的图像像素数据
	 ********************************************************/	
	public void scale(int[] src, int x, int y, int w, int h, int scansize,
	                  float scalex, float scaley, int[] dst) 
	{				
		//原图像的宽度
		int srcWidth = scansize;
		
		//原图像可以扫描的总行数:即原图像的高度
		int srcHeight = src.length / scansize;
		
		//width---height:处理区域的宽度和高度,
		//如果参数传递是合法的,那么它们就是w,h
		int width  = w;
		int height = h;

		if((x + w) > scansize)  width  = scansize  - x;
		if((y + h) > srcHeight) height = srcHeight - y;
	
		int dstWidth  = (int)( width * scalex + 0.5f);
		int dstHeight = (int)(height * scaley + 0.5f);

		//进行反向变换
		//i--按行,j--按列
		for(int i = 0;i < dstHeight;i++)
		{			
			//按反向变换法,获取第i行所对应的原图像的位置:行:yy
			float y_inverse_map = i / scaley;
			
			int y_lt = (int)y_inverse_map;
			
			//垂直方向偏移量
			float v = y_inverse_map - y_lt;
			
			//左上角的y坐标
			y_lt += y;
			
			int indexBase = i * dstWidth;
			for(int j = 0;j < dstWidth;j++)
			{
				float x_inverse_map = j / scalex;
			
				int x_lt = (int)x_inverse_map;
			
				//水平方向偏移量
				float u = x_inverse_map - x_lt;
			
				//左上角的y坐标
				x_lt += x;
				
				//通过计算获取变换后的点
				int index  = indexBase + j;
				dst[index] = interpolate(src, x_lt, y_lt, u, v, 
				                         srcWidth, srcHeight);
			}
		}
	}
	
	/************************************************************** 
	 * src:原图像的像素,
	 * (x,y):经过反向变换后,与反向变换点最接近的原图像的左上角的点
	 * (u,v):反向变换点相对(x,y)点的偏移量.
	 * scanw:原图像的扫描宽度,scanh原图像的高度
	 **************************************************************/
	private int interpolate(int[] src, int x, int y, float u, 
	                        float v, int scanw, int scanh)
	{		
		ColorModel colorModel = ColorModel.getRGBdefault();
		
		int r = 0;
		int g = 0;
		int b = 0;
		
		//邻近区域的像素值
		int red[][]   = new int[4][4];
		int green[][] = new int[4][4];
		int blue[][]  = new int[4][4];
		
		//邻近区域的坐标
		int xx[] = new int[4];
		int yy[] = new int[4];
		
		xx[0] = x - 1; xx[1] = x; xx[2] = x + 1; xx[3] = x + 2;
		yy[0] = y - 1; yy[1] = y; yy[2] = y + 1; yy[3] = y + 2;
		
		if(xx[0] < 0) xx[0] = 0;
		if(yy[0] < 0) yy[0] = 0;
		if(xx[2] > scanw - 1) xx[2] = scanw - 1;
		if(yy[2] > scanh - 1) yy[2] = scanh - 1;
		if(xx[3] > scanw - 1) xx[3] = scanw - 1;
		if(yy[3] > scanh - 1) yy[3] = scanh - 1;
	
		//获取4*4区域的像素值
		int i = 0; int j = 0;
		for(i = 0; i < 4; i++)
		{
			int indexBase = yy[i] * scanw;
			//j处理像素行
			for(j = 0; j < 4; j++)
			{
				int index   = indexBase + xx[j];
				red[i][j]   = colorModel.getRed(src[index]);
				green[i][j] = colorModel.getGreen(src[index]);
				blue[i][j]  = colorModel.getBlue(src[index]);
			}
		}
		
		float su[] = new float[4];
		float sv[] = new float[4];
		
		su[0] = sinx_x(1.0f + u);
		su[1] = sinx_x(u);
		su[2] = sinx_x(1.0f - u);
		su[3] = sinx_x(2.0f - u);

		sv[0] = sinx_x(1.0f + v);
		sv[1] = sinx_x(v);
		sv[2] = sinx_x(1.0f - v);
		sv[3] = sinx_x(2.0f - v);
		
		//作矩阵乘积:sv * red,sv * green,sv * blue
		float sv_r[] = new float[4]; 
		float sv_g[] = new float[4];
		float sv_b[] = new float[4];
		
		for(i = 0; i < 4; i++)
		{
			for(j = 0; j < 4; j++)
			{
				sv_r[i] += (sv[j] * red[j][i]);
				sv_g[i] += (sv[j] * green[j][i]);
				sv_b[i] += (sv[j] * blue[j][i]);
			}
		}
		
		r = (int)(su[0] * sv_r[0] + su[1] * sv_r[1] 
		  + su[2] * sv_r[2] + su[3] * sv_r[3]);
		g = (int)(su[0] * sv_g[0] + su[1] * sv_g[1] 
		  + su[2] * sv_g[2] + su[3] * sv_g[3]);
		b = (int)(su[0] * sv_b[0] + su[1] * sv_b[1] 
		  + su[2] * sv_b[2] + su[3] * sv_b[3]);
		
		r = (r < 0) ? 0 : ((r > 255) ? 255 : r);
		g = (g < 0) ? 0 : ((g > 255) ? 255 : g);
		b = (b < 0) ? 0 : ((b > 255) ? 255 : b);
		return (0xFF000000 | (( r << 16 ) | ( g << 8 ) | b ));
	}
	
	//计算 sin(x)/x 的值,采用多项式展开
	private float sinx_x(float x)
	{		
		float x_abs = Math.abs(x);
		float x_x   = x_abs * x_abs;
		float x_x_x = x_x * x_abs;
		
		if(x_abs < 1.0f)
			return (1.0f - 2.0f * x_x + x_x_x);
		else if(x_abs < 2.0f)
			return (4.0f - 8.0f * x_abs + 5.0f * x_x - x_x_x);
		else 
			return	0.0f;
	}

实验效果如下：