棋盘覆盖(递归分治问题)

 

在一个2^k * 2^k个方格组成的棋盘中，有一个方格与其它的不同，若使用以下四种L型骨牌覆盖除这个特殊方格的其它方格，如何覆盖。

 四各L型骨牌如下图1

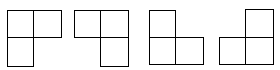
 图1  


棋盘中的特殊方格如图2

图2

    实现的基本原理是将2^k * 2^k的棋盘分成四块2^(k - 1) * 2^(k - 1)的子棋盘，特殊方格一定在其中的一个子棋盘中，如果特殊方格在某一个子棋盘中，继续递归处理这个子棋盘，直到这个子棋盘中只有一个方格为止如果特殊方格不在某一个子棋盘中，将这个子棋盘中的相应的位置设为骨牌号，将这个无特殊方格的了棋盘转换为有特殊方格的子棋盘，然后再递归处理这个子棋盘。以上原理如图3所示。

图3

 

    将棋盘保存在一个二维数组中。骨牌号从1开始，特殊方格为0，如果是一个4 * 4的棋盘，特殊方格为(2,2)，那么程序的输出为

 

2   2   3   3   
2   1   1   3   
4   1   0   5   
4   4   5   5 
相同数字的为同一骨牌。

=============================================================================

 

package 递归与分治;


public class ChessboardCoverage {

	private int tile = 1; //L型骨牌的值
	private int Board[][] = new int[16][16]; //表示棋盘
	
	/*
	 * tr:棋盘左上角方格的行号 tc:棋盘左上角方格的列号 dr:特殊方格所在的行号 dc:特殊方格所在的列号 size:方形棋盘的边长
	 */
	private void coverageChessBoard(int tr, int tc, int dr, int dc, int size) {
		if (size == 1)
			return;
		int t = tile++, s = size / 2;

		// 覆盖左上角子棋盘
		if (dr < tr + s && dc < tc + s)
			// 特殊方格在此棋盘中
			coverageChessBoard(tr, tc, dr, dc, s);
		else // 此棋盘无特殊方格
		{
			// 用t号L型骨型牌覆盖左上角子棋盘的右下角
			Board[tr + s - 1][tc + s - 1] = t;
			// 覆盖左上角的其余方格
			coverageChessBoard(tr, tc, tr + s - 1, tc + s - 1, s);
		}

		// 覆盖右上角子棋盘
		if (dr < tr + s && dc >= tc + s)
			coverageChessBoard(tr, tc + s, dr, dc, s);
		else {
			// 用t号L型骨型牌覆盖右上角子棋盘的左下角
			Board[tr + s - 1][tc + s] = t;
			// 覆盖右上角的其余方格
			coverageChessBoard(tr, tc + s, tr + s - 1, tc + s, s);
		}

		// 覆盖左下角子棋盘
		if (dr >= tr + s && dc < tc + s)
			coverageChessBoard(tr + s, tc, dr, dc, s);
		else {
			// 用t号L型骨型牌覆盖左下角子棋盘的右上角
			Board[tr + s][tc + s - 1] = t;
			// 覆盖左下角的其余方格
			coverageChessBoard(tr + s, tc, tr + s, tc + s - 1, s);
		}

		// 覆盖右下角子棋盘
		if (dr >= tr + s && dc >= tc + s)
			coverageChessBoard(tr + s, tc + s, dr, dc, s);
		else {
			// 用t号L型骨型牌覆盖右下角子棋盘的左上角
			Board[tr + s][tc + s] = t;
			// 覆盖右下角的其余方格
			coverageChessBoard(tr + s, tc + s, tr + s, tc + s, s);
		}
	}

	private void displayBoard(int size) {
		for (int i = 0; i < size; i++) {
			for (int j = 0; j < size; j++)
				System.out.printf("%4s", Board[i][j] + "");
			System.out.println();
		}
	}
	
	public static void main(String[] args) {
		ChessboardCoverage chessboardCoverage = new ChessboardCoverage();
		chessboardCoverage.coverageChessBoard(0, 0, 2, 2, 4);
		chessboardCoverage.displayBoard(4);
	}
}