- жµПиІИ: 243720 жђ°
- жАІеИЂ:

- жЭ•иЗ™: еМЧдЇђ
-

жЦЗзЂ†еИЖз±ї
з§ЊеМЇзЙИеЭЧ
- жИСзЪДиµДиЃѓ ( 0)
- жИСзЪДиЃЇеЭЫ ( 1)
- жИСзЪДйЧЃз≠Ф ( 1)
е≠Шж°£еИЖз±ї
- 2013-05 ( 7)
- 2013-04 ( 9)
- 2013-03 ( 13)
- жЫіе§Ъе≠Шж°£...
жЬАжЦ∞иѓДиЃЇ
зЃЧж≥Хз≥їеИЧдєЛеНБпЉЪзЫізЇњзФЯжИРзЃЧж≥Х
еЬ®жђІж∞ПеЗ†дљХз©ЇйЧідЄ≠пЉМеє≥йЭҐжЦєз®Ле∞±жШѓдЄАдЄ™дЄЙеЕГдЄАжђ°жЦєз®ЛпЉМзЫізЇње∞±жШѓдЄ§дЄ™йЭЮеє≥и°Меє≥йЭҐзЪДдЇ§зЇњпЉМжЙАдї•зЫізЇњжЦєз®Ле∞±жШѓдЄ§дЄ™дЄЙеЕГдЄАжђ°жЦєз®ЛзїДиБФзЂЛгАВдљЖжШѓеЬ®еє≥йЭҐиІ£жЮРеЗ†дљХдЄ≠пЉМзЫізЇњзЪДжЦєз®Ле∞±зЃАеНХзЪДе§ЪдЇЖгАВеє≥йЭҐеЗ†дљХдЄ≠зЫізЇњжЦєз®ЛжЬЙе§ЪзІН嚥еЉПпЉМдЄАиИђеЉПзЫізЇњжЦєз®ЛеПѓзФ®дЇОжППињ∞жЙАжЬЙзЫізЇњпЉЪ
Ax+By+C = 0 пЉИAгАБBдЄНеРМжЧґдЄЇ0пЉЙ
ељУзЯ•йБУзЫізЇњдЄКдЄАзВєеЭРж†ЗпЉИX0пЉМY0пЉЙеТМзЫізЇњзЪДжЦЬзОЗKе≠ШеЬ®жЧґпЉМеПѓдї•зФ®зВєжЦЬеЉПжЦєз®ЛпЉЪ
Y-Y0 = K(X вАУ X0) пЉИељУKдЄНе≠ШеЬ®жЧґпЉМзЫізЇњжЦєз®ЛзЃАеМЦжИРX = X0пЉЙ
ељУзЯ•йБУзЫізЇњдЄКзЪДдЄ§дЄ™зВє(X0,Y0)еТМ(X1,Y1)жЧґпЉМињШеПѓдї•зФ®дЄ§зВєеЉПжЦєз®ЛжППињ∞зЫізЇњпЉЪ
йЩ§дЇЖињЩдЄЙзІН嚥еЉПзЪДзЫізЇњжЦєз®Ле§ЦпЉМзЫізЇњжЦєз®ЛињШжЬЙжИ™иЈЭеЉПгАБжЦЬжИ™еЉПз≠Йе§ЪзІН嚥еЉПгАВ
еЬ®жХ∞е≠¶иМГзХіеЖЕзЪДзЫізЇњжШѓзФ±ж≤°жЬЙеЃљеЇ¶зЪДзВєзїДжИРзЪДйЫЖеРИпЉМдљЖжШѓеЬ®иЃ°зЃЧжЬЇеی嚥е≠¶зЪДиМГзХіеЖЕпЉМжЙАжЬЙзЪДеی嚥еМЕжЛђзЫізЇњйГљжШѓиЊУеЗЇжИЦжШЊз§ЇеЬ®зВєйШµиЃЊе§ЗдЄКзЪДпЉМ襀жИРдЄЇзВєйШµеی嚥жИЦеЕЙж†Ееی嚥гАВдї•жШЊз§ЇеЩ®дЄЇдЊЛпЉМзО∞еЃЮдЄ≠еЄЄиІБзЪДжШЊз§ЇеЩ®пЉИеМЕжЛђCRTжШЊз§ЇеЩ®еТМжґ≤жЩґжШЊз§ЇеЩ®пЉЙйГљеПѓдї•зЬЛжИРзФ±еРДзІНйҐЬиЙ≤еТМзБ∞еЇ¶еАЉзЪДеГПзі†зВєзїДжИРзЪДи±°зі†зЯ©йШµпЉМињЩдЇЫзВєжШѓжЬЙе§Іе∞ПзЪДпЉМиАМдЄФдљНзљЃеЫЇеЃЪпЉМеЫ†ж≠§еП™иГљињСдЉЉзЪДжШЊз§ЇеРДзІНеی嚥гАВеЫЊпЉИ1пЉЙе∞±жШѓеѓєињЩзІНжГЕеЖµзЪДдЄАзІНе§ЄеЉ†зЪДжФЊе§ІпЉЪ
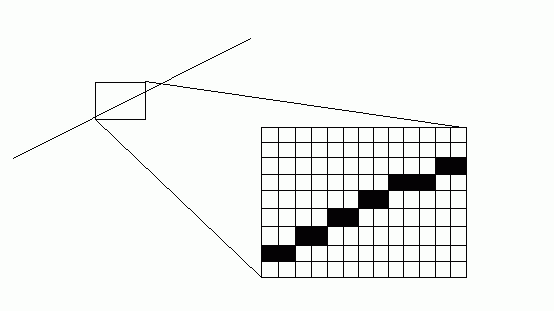
еЫЊпЉИ1пЉЙзЫізЇњеЬ®зВєйШµиЃЊе§ЗдЄКзЪДи°®зО∞嚥еЉП
иЃ°зЃЧжЬЇеی嚥е≠¶дЄ≠зЪДзЫізЇњзФЯжИРзЃЧж≥ХпЉМеЕґеЃЮеМЕеРЂдЇЖдЄ§е±ВжДПжАЭпЉМдЄАе±ВжШѓеЬ®иІ£жЮРеЗ†дљХз©ЇйЧідЄ≠ж†єжНЃеЭРж†ЗжЮДйА†еЗЇеє≥йЭҐзЫізЇњпЉМеП¶дЄАе±Ве∞±жШѓеЬ®еЕЙж†ЕжШЊз§ЇеЩ®дєЛз±їзЪДзВєйШµиЃЊе§ЗдЄКиЊУеЗЇдЄАдЄ™жЬАйАЉињСдЇОеی嚥зЪДи±°зі†зЫізЇњпЉМиАМињЩе∞±жШѓеЄЄиѓізЪДеЕЙж†Ееی嚥жЙЂжППиљђжНҐгАВжЬђжЦЗе∞±жШѓдїЛзїНеЗ†зІНеЄЄиІБзЪДзЫізЇњзФЯжИРзЪДеЕЙж†ЕжЙЂжППиљђжНҐзЃЧж≥ХпЉМеМЕжЛђжХ∞еАЉеЊЃеИЖж≥ХпЉИDDAж≥ХпЉЙгАБBresenhamзЃЧж≥ХгАБеѓєзІ∞зЫізЇњзФЯжИРзЃЧж≥Хдї•еПКдЄ§ж≠•зЃЧж≥ХгАВ
жХ∞еАЉеЊЃеИЖж≥ХпЉИDDAж≥ХпЉЙ
жХ∞еАЉеЊЃеИЖзФїзЇњзЃЧж≥ХпЉИDDAпЉЙж≥ХжШѓзЫізЇњзФЯжИРзЃЧж≥ХдЄ≠жЬАзЃАеНХзЪДдЄАзІНпЉМеЃГжШѓдЄАзІНеНХж≠•зЫізЇњзФЯжИРзЃЧж≥ХгАВеЃГзЪДзЃЧж≥ХжШѓињЩж†ЈзЪДпЉЪй¶ЦеЕИж†єжНЃзЫізЇњзЪДжЦЬзОЗз°ЃеЃЪжШѓдї•XжЦєеРСж≠•ињЫињШжШѓдї•YжЦєеРСж≠•ињЫпЉМзДґеРОж≤њзЭАж≠•ињЫжЦєеРСжѓПж≠•ињЫдЄАдЄ™зВєпЉИи±°зі†пЉЙпЉМе∞±ж≤њеП¶дЄАдЄ™еЭРж†ЗеПШйЗПkпЉМkжШѓзЫізЇњзЪДжЦЬзОЗпЉМеЫ†дЄЇжШѓеѓєзВєйШµиЃЊе§ЗиЊУеЗЇзЪДпЉМжЙАдї•йЬАи¶БеѓєжѓПжђ°иЃ°зЃЧеЗЇжЭ•зЪДдЄАеѓєеЭРж†ЗињЫи°МеЬЖжХігАВ
еЕЈдљУзЃЧж≥ХзЪДеЃЮзО∞пЉМйЩ§дЇЖеИ§жЦ≠жШѓжМЙзЕІXжЦєеРСињШжШѓжМЙзЕІYжЦєеРСж≠•ињЫдєЛе§ЦпЉМињШи¶БиАГиЩСзЫізЇњзЪДжЦєеРСпЉМдєЯе∞±жШѓиµЈзВєеТМзїИзВєзЪДеЕ≥з≥їгАВдЄЛйЭҐе∞±жШѓдЄАдЄ™жФѓжМБдїїжДПзЫізЇњжЦєеРСзЪДжХ∞еАЉеЊЃеИЖзФїзЇњзЃЧж≥ХеЃЮдЊЛпЉЪ
12void DDA_Line(int x1, int y1, int x2, int y2) 13{ 14 double k,dx,dy,x,y,xend,yend; 15 16 dx = x2 - x1; 17 dy = y2 - y1; 18 if(fabs(dx) >= fabs(dy)) 19 { 20 k = dy / dx; 21 if(dx > 0) 22 { 23 x = x1; 24 y = y1; 25 xend = x2; 26 } 27 else 28 { 29 x = x2; 30 y = y2; 31 xend = x1; 32 } 33 while(x <= xend) 34 { 35 SetDevicePixel((int)x, ROUND_INT(y)); 36 y = y + k; 37 x = x + 1; 38 } 39 40 } 41 else 42 { 43 k = dx / dy; 44 if(dy > 0) 45 { 46 x = x1; 47 y = y1; 48 yend = y2; 49 } 50 else 51 { 52 x = x2; 53 y = y2; 54 yend = y1; 55 } 56 while(y <= yend) 57 { 58 SetDevicePixel(ROUND_INT(x), (int)y); 59 x = x + k; 60 y = y + 1; 61 } 62 } 63} |
жХ∞еАЉеЊЃеИЖж≥ХпЉИDDAж≥ХпЉЙдЇІзФЯзЪДзЫізЇњжѓФиЊГз≤Њз°ЃпЉМиАМдЄФйАїиЊСзЃАеНХпЉМжШУдЇОзФ®з°ђдїґеЃЮзО∞пЉМдљЖжШѓж≠•ињЫйЗПxпЉМyеТМkењЕй°їзФ®жµЃзВєжХ∞и°®з§ЇпЉМжѓПдЄАж≠•йГљи¶БеѓєxжИЦyињЫи°МеЫЫиИНдЇФеЕ•еРОеПЦжХіпЉМдЄНеИ©дЇОеЕЙж†ЕеМЦжИЦзВєйШµиЊУеЗЇгАВ
BresenhamзЃЧж≥Х
BresenhamзЃЧж≥ХзФ±BresenhamеЬ®1965еєіжПРеЗЇзЪДдЄАзІНеНХж≠•зЫізЇњзФЯжИРзЃЧж≥ХпЉМжШѓиЃ°зЃЧжЬЇеی嚥е≠¶йҐЖеЯЯдљњзФ®жЬАеєњж≥ЫзЪДзЫізЇњжЙЂжППиљђжНҐзЃЧж≥ХгАВBresenhamзЃЧж≥ХзЪДеЯЇжЬђеОЯзРЖе∞±жШѓе∞ЖеЕЙж†ЕиЃЊе§ЗзЪДеРДи°МеРДеИЧи±°зі†дЄ≠ењГињЮжО•иµЈжЭ•жЮДйА†дЄАзїДиЩЪжЛЯзљСж†ЉзЇњгАВжМЙзЫізЇњдїОиµЈзВєеИ∞зїИзВєзЪДй°ЇеЇПиЃ°зЃЧзЫізЇњдЄОеРДеЮВзЫіжЦєеРСзљСж†ЉзЇњзЪДдЇ§зВєпЉМзДґеРОз°ЃеЃЪиѓ•еИЧи±°зі†дЄ≠дЄОж≠§дЇ§зВєжЬАињСзЪДи±°зі†гАВ

еЫЊпЉИ2пЉЙзЫізЇњBresenhamзЃЧж≥Хз§ЇжДПеЫЊ
еЫЊпЉИ2пЉЙе∞±е±Хз§ЇдЇЖињЩж†ЈдЄАзїДзљСж†ЉзЇњпЉМжѓПдЄ™дЇ§зВєе∞±дї£и°®зВєйШµиЃЊе§ЗдЄКзЪДдЄАдЄ™и±°зі†зВєпЉМзО∞еЬ®е∞±дї•еЫЊпЉИ2пЉЙдЄЇдЊЛдїЛзїНдЄАдЄЛBresenhamзЃЧж≥ХгАВељУзЃЧж≥ХдїОдЄАдЄ™зВєпЉИXiпЉМYiпЉЙж≤њзЭАXжЦєеРСеРСеЙНж≠•ињЫеИ∞Xi+1жЧґпЉМYжЦєеРСзЪДдЄЛдЄАдЄ™дљНзљЃеП™еПѓиГљжШѓYiеТМYi+1дЄ§зІНжГЕеЖµпЉМеИ∞еЇХжШѓYiињШжШѓYi+1еПЦеЖ≥дЇОеЃГдїђдЄОз≤Њз°ЃеАЉyзЪДиЈЭз¶їd1еТМd2еУ™дЄ™жЫіе∞ПгАВ
d1 = y - Yi пЉИз≠ЙеЉП 1пЉЙ
d2 = Yi+1 - y пЉИз≠ЙеЉП 2пЉЙ
ељУd1-d2 > 0жЧґпЉМYжЦєеРСзЪДдЄЛдЄАдЄ™дљНзљЃе∞ЖжШѓYi+1пЉМеР¶еИЩе∞±жШѓYiгАВзФ±ж≠§еПѓиІБпЉМBresenhamзЃЧж≥ХеЕґеЃЮеТМжХ∞еАЉеЊЃеИЖзЃЧж≥ХеОЯзРЖжШѓдЄАж†ЈзЪДпЉМеЈЃеИЂеЬ®дЇОBresenhamзЃЧж≥ХдЄ≠з°ЃеЃЪYжЦєеРСдЄЛдЄАдЄ™зВєзЪДдљНзљЃзЪДеИ§жЦ≠жЭ°дїґзЪДиЃ°зЃЧжЦєеЉПдЄНдЄАж†ЈгАВзО∞еЬ®е∞±жЭ•еИЖжЮРдЄАдЄЛињЩдЄ™еИ§жЦ≠жЭ°дїґзЪДиЃ°зЃЧжЦєж≥ХпЉМеЈ≤зЯ•зЫізЇњзЪДжЦЬзОЗkеТМеЬ®yиљізЪДжИ™иЈЭbпЉМеПѓжО®еѓЉеЗЇXi+1дљНзљЃзЪДз≤Њз°ЃеАЉyе¶ВдЄЛпЉЪ
y = k Xi+1 + b пЉИз≠ЙеЉП 3пЉЙ
е∞Жз≠ЙеЉП 1-3еЄ¶еЕ•d1-d2пЉМеПѓеЊЧеИ∞з≠ЙеЉП4пЉЪ
зЪД
d1-d2 = 2k Xi+1 - Yi - Yi+1 + 2b пЉИз≠ЙеЉП 4пЉЙ
жЬЙеЫ†дЄЇж†єжНЃеЫЊпЉИ2пЉЙжЭ°дїґпЉМk = dy / dxпЉМYi+1 = Yi + 1пЉМXi+1 =Xi + 1пЉМе∞Жж≠§дЄЙдЄ™еЕ≥з≥їеЄ¶еЕ•з≠ЙеЉП4пЉМеРМжЧґеЬ®з≠ЙеЉПдЄ§иЊєдєШдї•dxпЉМжХізРЖеРОеПѓеЊЧеИ∞з≠ЙеЉП5пЉЪ
dx(d1 вАУ d2) = 2dyXi + 2dy - 2dxYi + dx(2b - 1) пЉИз≠ЙеЉП 5пЉЙ
еП¶pi = dx(d1 вАУ d2)пЉМеИЩпЉЪ
pi = 2dyXi + 2dy - 2dxYi + dx(2b - 1)
еЫ†дЄЇеЫЊпЉИ2пЉЙзЪДз§ЇдЊЛdxжШѓе§ІдЇО0зЪДеАЉпЉМеЫ†ж≠§piзЪДзђ¶еПЈдЄО(d1 вАУ d2)дЄАиЗіпЉМзО∞еЬ®е∞ЖеИЭеІЛжЭ°дїґеЄ¶еЕ•еПѓеЊЧеИ∞жЬАеИЭзЪДзђђдЄАдЄ™еИ§жЦ≠жЭ°дїґp1пЉЪ
p1 = 2dy вАУ dx
ж†єжНЃXi+1дЄОXiпЉМдї•еПКYi+1дЄОYiзЪДеЕ≥з≥їпЉМеПѓдї•жО®еЗЇpiзЪДйАТжО®еЕ≥з≥їпЉЪ
pi+1 = pi + 2dy - 2dx(yi+1 - yi)
зФ±дЇОyi+1еПѓиГљжШѓyiпЉМдєЯеПѓиГљжШѓyi + 1пЉМеЫ†ж≠§пЉМpi+1е∞±еПѓиГљжШѓдї•дЄЛдЄ§зІНеПѓиГљпЉМеєґдЄФеТМyiзЪДеПЦеАЉжШѓеѓєеЇФзЪДпЉЪ
pi+1 = pi + 2dy пЉИYжЦєеРСдњЭжМБеОЯеАЉпЉЙ
жИЦ
pi+1 = pi + 2(dy вАУ dx) пЉИYжЦєеРСеРСеЙНж≠•ињЫ1пЉЙ
ж†єжНЃдЄКйЭҐзЪДжО®еѓЉпЉМељУx2 > x1пЉМy2 > y1жЧґBresenhamзЫізЇњзФЯжИРзЃЧж≥ХзЪДиЃ°зЃЧињЗз®Ле¶ВдЄЛпЉЪ
1гАБзФїзВє(x1, y1); иЃ°зЃЧиѓѓеЈЃеИЭеАЉp1=2dy-dxпЉЫ
2гАБж±ВзЫізЇњзЪДдЄЛдЄАзВєдљНзљЃпЉЪ
Xi+1 = Xi+1пЉЫ
е¶ВжЮЬ pi > 0 еИЩYi+1 = Yi + 1пЉЫ
еР¶еИЩYi+1 = YiпЉЫ
зФїзВє(Xi+1, Yi+1 )пЉЫ
3гАБж±ВдЄЛдЄАдЄ™иѓѓеЈЃpi+1пЉЫ
е¶ВжЮЬ pi>0 еИЩpi+1 = pi+2(dy вАУ dx);
еР¶еИЩpi+1 = pi+2dyпЉЫ
4гАБе¶ВжЮЬж≤°жЬЙзїУжЭЯпЉМеИЩиљђеИ∞ж≠•й™§2пЉЫеР¶еИЩзїУжЭЯзЃЧж≥ХгАВ
дЄЛйЭҐе∞±зїЩеЗЇйТИеѓєдЄКйЭҐжО®еѓЉеЗЇзЪДзЃЧж≥ХжЇРдї£з†БпЉИеП™жФѓжМБ x2 > x1пЉМy2 > y1зЪДжГЕеЖµпЉЙпЉЪ
319void Bresenham_Line(int x1, int y1, int x2, int y2) 320{ 321 int dx = abs(x2 - x1); 322 int dy = abs(y2 - y1); 323 int p = 2 * dy - dx; 324 int x = x1; 325 int y = y1; 326 327 while(x <= x2) 328 { 329 SetDevicePixel(x, y); 330 x++; 331 if(p<0) 332 p += 2 * dy; 333 else 334 { 335 p += 2 * (dy - dx); 336 y += 1; 337 } 338 } 339} |
дЄКйЭҐзЪДдї£з†БеП™жШѓжЉФз§ЇиЃ°зЃЧињЗз®ЛпЉМзЬЯж≠£еЃЮзФ®зЪДдї£з†Би¶БжФѓжМБеРДзІНжЦєеРСзЪДзЫізЇњзФЯжИРпЉМињЩе∞±и¶БиАГиЩСжЦЬзОЗдЄЇиіЯеАЉзЪДжГЕеЖµдї•еПКx1 > x2зЪДжГЕеЖµпЉМеП¶е§ЦпЉМеЊ™зОѓдЄ≠зЪДдЄ§жђ°дєШж≥ХињРзЃЧеПѓдї•еЬ®еЊ™зОѓе§ЦиЃ°зЃЧеЗЇжЭ•пЉМдЄНењЕжѓПжђ°йГљиЃ°зЃЧгАВи¶БжФѓжМБеРДзІНжЦєеРСзЪДзЫізЇњзФЯжИРеЕґеЃЮдєЯеЊИзЃАеНХпЉМе∞±жШѓйАЪињЗеЭРж†ЗдЇ§жНҐпЉМдљњдєЛзђ¶еРИдЄКйЭҐжЉФз§ЇзЃЧж≥ХзЪДи¶Бж±ВеН≥еПѓпЉМдЄЛйЭҐе∞±жШѓдЄАдЄ™еЃЮзФ®зЪДпЉМжФѓжМБеРДзІНжЦєеРСзЪДзЫізЇњзФЯжИРзЪДBresenhamзЃЧж≥ХпЉЪ
164void Bresenham_Line(int x1, int y1, int x2, int y2) 165{ 166 int dx,dy,p,const1,const2,x,y,inc; 167 168 int steep = (abs(y2 - y1) > abs(x2 - x1)) ? 1 : 0; 169 if(steep == 1) 170 { 171 SwapInt(&x1, &y1); 172 SwapInt(&x2, &y2); 173 } 174 if(x1 > x2) 175 { 176 SwapInt(&x1, &x2); 177 SwapInt(&y1, &y2); 178 } 179 dx = abs(x2 - x1); 180 dy = abs(y2 - y1); 181 p = 2 * dy - dx; 182 const1 = 2 * dy; 183 const2 = 2 * (dy - dx); 184 x = x1; 185 y = y1; 186 187 inc = (y1 < y2) ? 1 : -1; 188 while(x <= x2) 189 { 190 if(steep == 1) 191 SetDevicePixel(y, x); 192 else 193 SetDevicePixel(x, y); 194 x++; 195 if(p<0) 196 p += const1; 197 else 198 { 199 p += const2; 200 y += inc; 201 } 202 } 203} |
BresenhamзЃЧж≥ХеП™еЃЮзФ®жХіжХ∞иЃ°зЃЧпЉМе∞СйЗПзЪДдєШж≥ХињРзЃЧйГљеПѓдї•йАЪињЗзІїдљНжЭ•йБњеЕНпЉМеЫ†ж≠§иЃ°зЃЧйЗПе∞СпЉМжХИзОЗйЂШпЉМ
еѓєзІ∞зЫізЇњзФЯжИРзЃЧж≥Х(жФєињЫзЪДBresenhamзЃЧж≥Х)
зЫізЇњжЃµжЬЙдЄ™зЙєжАІпЉМйВ£е∞±жШѓзЫізЇњжЃµзЫЄеѓєдЇОдЄ≠ењГзВєжШѓдЄ§иЊєеѓєзІ∞зЪДгАВеЫ†ж≠§еПѓдї•еИ©зФ®ињЩдЄ™еѓєзІ∞жАІпЉМеѓєеЕґеЃГеНХж≠•зЫізЇњзФЯжИРзЃЧж≥ХињЫи°МжФєињЫпЉМдљњеЊЧжѓПињЫи°МдЄАжђ°еИ§жЦ≠жИЦзЫЄеЕ≥иЃ°зЃЧеПѓдї•зФЯжИРзЫЄеѓєдЇОзЫізЇњдЄ≠зВєзЪДдЄ§дЄ™еѓєзІ∞зВєгАВе¶Вж≠§дї•жЭ•пЉМзЫізЇње∞±зФ±дЄ§зЂѓеРСдЄ≠йЧізФЯжИРгАВдїОзРЖиЃЇдЄКиЃ≤пЉМињЩдЄ™жФєињЫеПѓдї•еЇФзФ®дЇОдїїдљХдЄАзІНеНХж≠•зЫізЇњзФЯжИРзЃЧж≥ХпЉМжЬђдЊЛе∞±еП™жШѓеѓєBresenhamзЃЧж≥ХињЫи°МжФєињЫгАВ
жФєињЫдЄїи¶БйЫЖдЄ≠еЬ®дї•дЄЛеЗ†зВєпЉМй¶ЦеЕИжШѓеЊ™зОѓеМЇйЧіпЉМзФ±[x1, x2]дњЃжФєжИР[x1, half]пЉМhalfжШѓеМЇйЧі[x1, x2]зЪДдЄ≠зВєгАВеЕґжђ°жШѓXиљізЪДж≠•ињЫжЦєеРСжФєжИРеПМеРСпЉМжЬАеРОжШѓYжЦєеРСзЪДеАЉи¶БеѓєзІ∞дњЃжФєпЉМйЩ§ж≠§дєЛе§ЦпЉМзЃЧж≥ХжХідљУзїУжЮДдЄНеПШпЉМдЄЛйЭҐе∞±жШѓжФєињЫеРОзЪДдї£з†БпЉЪ
205void Sym_Bresenham_Line(int x1, int y1, int x2, int y2) 206{ 207 int dx,dy,p,const1,const2,xs,ys,xe,ye,half,inc; 208 209 int steep = (abs(y2 - y1) > abs(x2 - x1)) ? 1 : 0; 210 if(steep == 1) 211 { 212 SwapInt(&x1, &y1); 213 SwapInt(&x2, &y2); 214 } 215 if(x1 > x2) 216 { 217 SwapInt(&x1, &x2); 218 SwapInt(&y1, &y2); 219 } 220 dx = x2 - x1; 221 dy = abs(y2 - y1); 222 p = 2 * dy - dx; 223 const1 = 2 * dy; 224 const2 = 2 * (dy - dx); 225 xs = x1; 226 ys = y1; 227 xe = x2; 228 ye = y2; 229 half = (dx + 1) / 2; 230 inc = (y1 < y2) ? 1 : -1; 231 while(xs <= half) 232 { 233 if(steep == 1) 234 { 235 SetDevicePixel(ys, xs); 236 SetDevicePixel(ye, xe); 237 } 238 else 239 { 240 SetDevicePixel(xs, ys); 241 SetDevicePixel(xe, ye); 242 } 243 xs++; 244 xe--; 245 if(p<0) 246 p += const1; 247 else 248 { 249 p += const2; 250 ys += inc; 251 ye -= inc; 252 } 253 } 254} |
дЄ§ж≠•зЃЧж≥Х
дЄ§ж≠•зЃЧж≥ХжШѓеЬ®зФЯжИРзЫізЇњзЪДињЗз®ЛдЄ≠пЉМжѓПжђ°еИ§жЦ≠йГљзФЯжИРдЄ§дЄ™зВєзЪДзЫізЇњзФЯжИРзЃЧж≥ХгАВдЄКдЄАиКВдїЛзїНзЪДеѓєзІ∞зЫізЇњзФЯжИРжЦєж≥ХдєЯжШѓжѓПжђ°зФЯжИРдЄ§дЄ™зВєпЉМдљЖжШѓеЃГеТМдЄ§ж≠•зЃЧж≥ХзЪДеМЇеИЂе∞±жШѓеѓєзІ∞жЦєж≥ХзЪДиЃ°зЃЧеТМеИ§жЦ≠жШѓдїОзЇњжЃµзЪДдЄ§зЂѓеРСдЄ≠зВєињЫи°МпЉМиАМдЄ§ж≠•зЃЧж≥ХжШѓж≤њзЭАдЄАдЄ™жЦєеРСпЉМдЄАжђ°зФЯжИРдЄ§дЄ™зВєгАВ
ељУжЦЬзОЗkжї°иґ≥жЭ°дїґ0вЙ§kпЉЬ1жЧґпЉМеБЗе¶ВељУеЙНзВєPеЈ≤зїПз°ЃеЃЪпЉМе¶ВеЫЊпЉИ3пЉЙжЙАз§ЇпЉМеИЩPдєЛеРОзЪДињЮзї≠дЄ§дЄ™зВєеП™еПѓиГљжШѓеЫЫзІНжГЕеЖµпЉЪABпЉМACпЉМDCеТМDEпЉМдЄ§ж≠•зЃЧж≥ХиЃЊзЂЛеЖ≥з≠ЦйЗПeдљЬдЄЇеИ§жЦ≠ж†ЗењЧпЉМeзЪДеИЭеІЛеАЉжШѓ4dy вАУ dxпЉМеЕґдЄ≠пЉЪ
dy = y2 вАУ y1
dx = x2 вАУ x1гАВ
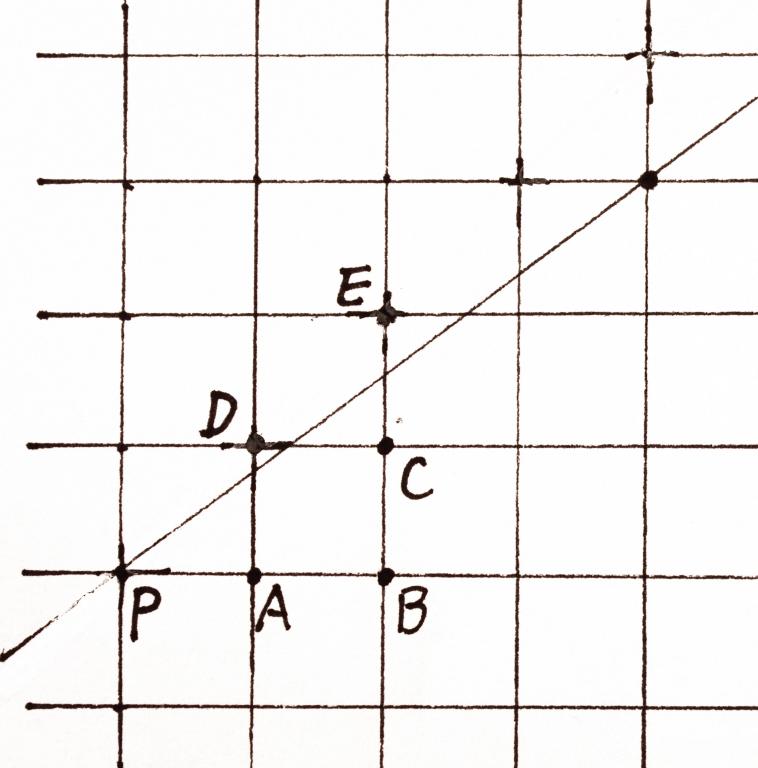
еЫЊпЉИ3пЉЙзЫізЇњдЄ§ж≠•зЃЧж≥Хз§ЇжДПеЫЊ
дЄЇзЃАеНХиµЈиІБпЉМеЕИиАГиЩСdy > dx > 0ињЩзІНжГЕеЖµгАВељУe > 2dxжЧґпЉМPеРОдЄ§дЄ™зВєе∞ЖдЉЪжШѓDEзїДеРИпЉМж≠§жЧґeзЪДеҐЮйЗПжШѓ4dy вАУ 4dxгАВељУdx < e < 2dxжЧґпЉМPеРОзЪДдЄ§дЄ™зВєе∞ЖдЉЪжШѓDCзїДеРИпЉМж≠§жЧґeзЪДеҐЮйЗПжШѓ4dy вАУ 2dx.гАВељУ0 < e < dxжЧґпЉМPеРОзЪДдЄ§дЄ™зВєе∞ЖдЉЪжШѓACзїДеРИпЉМж≠§жЧґeзЪДеҐЮйЗПжШѓ4dy вАУ 2dx.гАВељУe < 0жЧґпЉМPеРОзЪДдЄ§дЄ™зВєе∞ЖдЉЪжШѓABзїДеРИпЉМж≠§жЧґeзЪДеҐЮйЗПжШѓ4dyгАВзїЉеРИдї•дЄКжППињ∞пЉМељУжЦЬзОЗkжї°иґ≥жЭ°дїґ0вЙ§kпЉЬ1пЉМдЄФdy > dx > 0ињЩзІНжГЕеЖµдЄЛпЉМдЄ§ж≠•зЃЧж≥ХеПѓдї•ињЩж†ЈеЃЮзО∞пЉЪ
257void Double_Step_Line(int x1, int y1, int x2, int y2) 258{ 259 int dx = x2 - x1; 260 int dy = y2 - y1; 261 int e = dy * 4 - dx; 262 int x = x1; 263 int y = y1; 264 265 SetDevicePixel(x, y); 266 267 while(x < x2) 268 { 269 if (e > dx) 270 { 271 if (e > ( 2 * dx)) 272 { 273 e += 4 * (dy - dx); 274 x++; 275 y++; 276 SetDevicePixel(x, y); 277 x++; 278 y++; 279 SetDevicePixel(x, y); 280 } 281 else 282 { 283 e += (4 *dy - 2 * dx); 284 x++; 285 y++; 286 SetDevicePixel(x, y); 287 x++; 288 SetDevicePixel(x, y); 289 } 290 } 291 else 292 { 293 if (e > 0) 294 { 295 e += (4 * dy - 2 * dx); 296 x++; 297 SetDevicePixel(x, y); 298 x++; 299 y++; 300 SetDevicePixel(x, y); 301 } 302 else 303 { 304 x++; 305 SetDevicePixel(x, y); 306 x++; 307 SetDevicePixel(x, y); 308 e += 4 * dy; 309 } 310 } 311 } 312} |
дї•дЄКеЗљжХ∞йЩ§дЇЖеП™жФѓжМБдЄАдЄ™жЦєеРСзЪДзЫізЇњзФЯжИРдєЛе§ЦпЉМињШжЬЙеЕґеЃГдЄНеЃМеЦДзЪДеЬ∞жЦєпЉМжѓФе¶Вж≤°жЬЙеИ§жЦ≠жЬАеРОдЄАдЄ™зВєжШѓеР¶дЉЪиґКзХМпЉМе§ІйЗПеЗЇзО∞зЪДдєШж≥ХиЃ°зЃЧеПѓдї•зФ®зІїдљНе§ДзРЖз≠Йз≠ЙгАВдїњзЕІBresenhamзЃЧж≥ХдЄАиКВдїЛзїНзЪДжЦєж≥ХпЉМеЊИеЃєжШУе∞ЖеЕґжЙ©е±ХдЄЇжФѓжМБ8дЄ™жЦєеРСзЪДзЫізЇњзФЯжИРпЉМеЫ†дЄЇдї£з†БжѓФиЊГйХњпЉМињЩйЗМе∞±дЄНеИЧеЗЇдї£з†БдЇЖгАВ
жАїзїУ
йЩ§дЇЖдї•дЄКдїЛзїНзЪДеЗ†зІНзЫізЇњзФЯжИРзЃЧж≥ХпЉМињШжЬЙеЊИе§ЪеЕґеЃГзЪДзЫізЇњеЕЙж†ЕжЙЂжППиљђжНҐзЃЧж≥ХпЉМжѓФе¶ВдЄЙж≠•зЃЧж≥ХгАБеЫЫж≠•зЃЧж≥ХгАБдЄ≠зВєеИТзЇњж≥Хз≠Йз≠ЙпЉМињШжЬЙдЇЇе∞ЖдЄЙж≠•зЃЧж≥ХзїУеРИеЙНйЭҐдїЛзїНзЪДеѓєзІ∞ж≥ХжПРеЗЇдЇЖдЄАзІНеПѓдї•дЄАжђ°зФїеЕ≠дЄ™зВєзЪДзЫізЇњзФЯжИРзЃЧж≥ХпЉМињЩйЗМе∞±дЄНе§ЪдїЛзїНдЇЖпЉМжЬЙеЕіиґ£зЪДиѓїиАЕеПѓдї•жЙЊиЃ°зЃЧжЬЇеی嚥е≠¶зЪДзЫЄеЕ≥иµДжЦЩжЭ•дЇЖиІ£еЕЈдљУзЪДеЖЕеЃєгАВ
жЬђжЦЗдїЛзїНзЪДеЗ†зІНзЫізЇњзФЯжИРзЃЧж≥ХдЄ≠пЉМDDAзЃЧж≥ХжЬАзЃАеНХпЉМдљЖжШѓеЫ†дЄЇжЬЙе§Ъжђ°жµЃзВєжХ∞дєШж≥ХеТМйЩ§ж≥ХињРзЃЧпЉМдї•еПКжµЃзВєжХ∞еЬЖжХіињРзЃЧпЉМжХИзОЗжѓФиЊГдљОгАВBresenhamзЃЧж≥ХдЄ≠зЪДжХіжХ∞дєШж≥ХиЃ°зЃЧйГљеПѓдї•зФ®зІїдљНдї£жЫњпЉМдЄїи¶БињРзЃЧйГљйЗЗзФ®дЇЖжХіжХ∞еК†ж≥ХеТМеЗПж≥ХињРзЃЧпЉМеЫ†ж≠§жХИзОЗжѓФиЊГйЂШпЉМеРДзІНеРДж†ЈеПШ嚥зЪДBresenhamзЃЧж≥ХеЬ®иЃ°зЃЧжЬЇеی嚥蚃俴дЄ≠еЊЧеИ∞дЇЖеєњж≥ЫзЪДеЇФзФ®гАВзРЖиЃЇдЄКиЃ≤пЉМдЄ§ж≠•зЃЧж≥Хдї•еПКеЫЫж≠•зЃЧж≥ХжХИзОЗеЇФиѓ•жЫійЂШдЄАдЇЫпЉМдљЖжШѓињЩдЄ§зІНзЃЧж≥ХйЬАи¶БеБЪжѓФиЊГе§ЪзЪДеЗЖе§ЗеЈ•дљЬпЉМдЄФе§ЪжШѓдєШж≥ХеТМйЩ§ж≥ХињРзЃЧпЉМеЫ†ж≠§еЬ®зФЯжИРжѓФиЊГзЯ≠зЪДзЫізЇњжЧґпЉМжХИзОЗеПНиАМдЄНе¶ВBresenhamзЃЧж≥ХгАВ
еПВиАГиµДжЦЩпЉЪ
гАР1гАСиЃ°зЃЧеЗ†дљХпЉЪзЃЧж≥ХиЃЊиЃ°дЄОеИЖжЮР еС®еЯєеЊЈ жЄЕеНОе§Іе≠¶еЗЇзЙИз§Њ 2005еєі
гАР2гАСиЃ°зЃЧеЗ†дљХпЉЪзЃЧж≥ХдЄОеЇФзФ® еЊЈиіЭе∞ФиµЂпЉИйВУдњКиЊЙиѓСпЉЙ жЄЕеНОе§Іе≠¶еЗЇзЙИз§Њ 2005еєі
гАР3гАСиЃ°зЃЧжЬЇеی嚥е≠¶ е≠ЩеЃґеєњгАБжЭ®еЄЄиіµ жЄЕеНОе§Іе≠¶еЗЇзЙИз§Њ 1995еєі
- 2012-01-08 23:41
- жµПиІИ 334
- иѓДиЃЇ(0)
- жЯ•зЬЛжЫіе§Ъ







зЫЄеЕ≥жО®иНР
BresenhamзЫізЇњзФЯжИРзЃЧж≥ХжШѓзЫЃеЙНжЬАеЄЄзФ®зЪДдЄАзІНзЫізЇњзїШеИґзЃЧж≥ХпЉМзФ±Jack E. BresenhamдЇО1965еєіжПРеЗЇгАВеЃГеЯЇдЇОиѓѓеЈЃзіѓзІѓзЪДж¶ВењµпЉМдї•жЬАе∞ПзЪДиЃ°зЃЧйЗПеТМеЖЕе≠ШйЬАж±ВжЭ•ињСдЉЉзїШеИґзЫізЇњгАВзЃЧж≥ХзЪДдЄїи¶Бж≠•й™§е¶ВдЄЛпЉЪ 1. еИЭеІЛеМЦдЄ§дЄ™еПШйЗПпЉМx_errorи°®з§Їx...
### зЫізЇњзФЯжИРзЃЧж≥Х 1. **DDAпЉИDigital Differential AnalyzerпЉЙзЃЧж≥Х**пЉЪжШѓжЬАзЃАеНХзЪДзЫізЇњзФЯжИРзЃЧж≥ХгАВеЃГйАЪињЗе∞ЖзЫізЇњзЪДиµЈзВєеТМзїИзВєеЭРж†ЗиљђжНҐдЄЇжХіжХ∞пЉМеєґдї•жБТеЃЪзЪДж≠•йХњж≤њзЭАxиљіеТМyиљіињЫи°МйАТеҐЮпЉМзЫіеИ∞иЊЊеИ∞зїИзВєгАВињЩзІНжЦєж≥ХиЃ°зЃЧзЃАеНХпЉМ...
5. зЫізЇњзФЯжИРзЃЧж≥ХпЉЪзЫізЇњзФЯжИРзЃЧж≥ХжШѓиЃ°зЃЧжЬЇеی嚥е≠¶дЄ≠зЪДеЯЇжЬђзЃЧж≥ХпЉМеМЕжЛђжХ∞еАЉеЊЃеИЖж≥ХпЉИDDAпЉЙгАБдЄ≠зВєзФїзЇњзЃЧж≥ХеТМBresenhamзФїзЇњзЃЧж≥ХгАВињЩдЇЫзЃЧж≥ХеПѓдї•зФЯжИРзЫізЇњгАБеЬЖеТМеЕґдїЦеی嚥гАВ 6. дЄ≠зВєзФїзЇњзЃЧж≥ХпЉЪдЄ≠зВєзФїзЇњзЃЧж≥ХжШѓзЫізЇњзФЯжИРзЃЧж≥ХзЪДдЄАзІН...
### зЫізЇњзФЯжИРзЃЧж≥ХеЃЮй™МжК•еСКзЯ•иѓЖзВєиІ£жЮР #### еЃЮй™МиГМжЩѓдЄОзЫЃж†З жЬђжђ°еЃЮй™МзЪДдЄїи¶БзЫЃзЪДжШѓиЃ©е≠¶зФЯйАЪињЗеЃЮйЩЕзЉЦз®ЛжУНдљЬпЉМжЈ±еЕ•зРЖиІ£еєґзЖЯзїГжОМжП°зЫізЇњзЪДзФЯжИРзЃЧж≥ХпЉМе∞§еЕґжШѓBresenhamзЫізЇњзФЯжИРзЃЧж≥ХгАВйАЪињЗеЃЮй™МпЉМе≠¶зФЯйЬАи¶БжОМжП°дї•дЄЛжКАиГљпЉЪ 1....
еЬ®иЃ°зЃЧжЬЇеی嚥е≠¶дЄ≠пЉМзЫізЇњзФЯжИРзЃЧж≥ХжШѓиЗ≥еЕ≥йЗНи¶БзЪДдЄАдЄ™йГ®еИЖпЉМзФ®дЇОеЬ®е±ПеєХдЄКзїШеИґзЫізЇњгАВжЬђй°єзЫЃдЄїи¶БжОҐиЃ®дЇЖвАЬзЫізЇњзФЯжИРзЃЧж≥ХвАЭпЉМеєґдЄФдљњзФ®C++зЉЦз®Лиѓ≠и®АпЉИVC++зОѓеҐГпЉЙеЃЮзО∞дЇЖеЕґдЄ≠зЪДдЄ≠зВєзФїзЇњзЃЧж≥ХпЉИMidpoint Drawing AlgorithmпЉЙпЉМињЩдєЯ...
жЬЙе§ЪзІНзЃЧж≥ХеПѓдї•еЃЮзО∞зЫізЇњзЪДзїШеИґпЉМжЬђжЦЗе∞Жиѓ¶зїЖдїЛзїНдЄЙзІНеЄЄзФ®зЪДзЫізЇњзЃЧж≥ХпЉЪDDAзЃЧж≥ХгАБдЄ≠зВєзЃЧж≥ХеТМBresenhamзЃЧж≥ХгАВ DDAзЃЧж≥Х DDAпЉИDigital Differential AnalyzerпЉЙзЃЧж≥ХжШѓдЄАзІНзЃАеНХзЪДзЫізЇњзЃЧж≥ХпЉМеЃГеЯЇдЇОзЫізЇњзЪДжЦЬзОЗжЭ•з°ЃеЃЪжѓПдЄ™...
еЬ®иЃ°зЃЧжЬЇеی嚥е≠¶дЄ≠пЉМзЫізЇњзФЯжИРзЃЧж≥ХжШѓеЯЇз°АдЄФиЗ≥еЕ≥йЗНи¶БзЪДпЉМеЃГдљњеЊЧиЃ°зЃЧжЬЇиГље§Яз≤Њз°ЃеЬ∞жППзїШеЗЇзЫізЇњпЉМдЄЇе§НжЭВзЪДеی嚥жЄ≤жЯУеТМеЫЊеГПе§ДзРЖжПРдЊЫеЯЇз°АгАВеЬ®WindowsзЉЦз®ЛзОѓеҐГдЄ≠пЉМVC++пЉИVisual C++пЉЙ媪襀зФ®дЇОеЉАеПСеی嚥еЇФзФ®пЉМеЫ†ж≠§зРЖиІ£еєґжОМжП°зЫізЇњ...
"иЃ°зЃЧжЬЇеی嚥е≠¶-дЄЙзІНзЫізЇњзФЯжИРзЃЧж≥ХеПКеЬЖзЪДзФЯжИРзЃЧж≥Х" иЃ°зЃЧжЬЇеی嚥е≠¶жШѓиЃ°зЃЧжЬЇзІСе≠¶дЄОжКАжЬѓе≠¶йЩҐдЄ≠зЪДдЄАдЄ™йЗНи¶БжЦєеРСпЉМеЃГжґЙеПКеИ∞иЃ°зЃЧжЬЇеی嚥зЪДзФЯжИРгАБжШЊз§ЇеТМе§ДзРЖгАВеЬ®иЃ°зЃЧжЬЇеی嚥е≠¶дЄ≠пЉМзЫізЇњеТМеЬЖжШѓжЬАеЯЇжЬђзЪДеی嚥еЕГзі†пЉМжЬђжЦЗе∞ЖдїЛзїНдЄЙзІН...
2. жОМжП°еЗ†зІНеЯЇжЬђзЪДзЫізЇњзФЯжИРзЃЧж≥ХпЉЪDDA зЃЧж≥ХгАБBresenham зФїзЇњж≥ХгАБдЄ≠зВєзФїзЇњж≥Х 3. еЃЮзО∞зЫізЇњзФЯжИРзЪДпЉМеЬ®е±ПеєХдЄКдїїжДПзФЯжИРдЄАжЭ°зЫізЇњ дЄЙгАБеЃЮзО∞з®ЛеЇПпЉЪ жЬђеЃЮй™МдљњзФ® C иѓ≠и®АзЉЦеЖЩпЉМдљњзФ® Borland Graphics InterfaceпЉИBGIпЉЙеЇУжЭ•еЃЮзО∞...
### DDAзЫізЇњзФЯжИРзЃЧж≥ХеПКеЕґCиѓ≠и®АеЃЮзО∞ #### DDAзЃЧж≥ХзЃАдїЛ жХ∞е≠ЧеЈЃеИЖеИЖжЮРеЩ®пЉИDigital Differential AnalyzerпЉМзЃАзІ∞DDAпЉЙжШѓдЄАзІНзФ®дЇОиЃ°зЃЧжЬЇеی嚥е≠¶дЄ≠зЪДеЯЇжЬђзїШеЫЊзЃЧж≥ХдєЛдЄАпЉМдЄїи¶БзФ®дЇОзФЯжИРзЫізЇњжЃµгАВеЃГйАЪињЗйАРж≠•зіѓеК†жЦЬзОЗзЪДжЦєеЉПиЃ°зЃЧ...
еЃЮй™МзЪДдЄїи¶БзЫЃж†ЗжШѓжОМжП°3зІНеЄЄиІБзЪДзЫізЇњзФЯжИРзЃЧж≥ХпЉЪжХ∞еАЉеЊЃеИЖпЉИDDAпЉЙзЃЧж≥ХгАБдЄ≠зВєзЃЧж≥Хдї•еПКBresenhamзЃЧж≥ХпЉМеєґиГље§ЯеЬ®MFCзОѓеҐГдЄЛж≠£з°ЃзїШеИґзЫізЇњгАВ **1. DDAпЉИDigital Differential AnalyzerпЉЙзЃЧж≥Х** DDAзЃЧж≥ХеЯЇдЇОзЫізЇњжЦєз®Лy = kx +...
VC 6.0 жЉФз§ЇдЄАзІНзЫізЇњзФЯжИРзЪДзЃЧж≥ХпЉМжЉФз§ЇдЇЖдЄЙзІНзЫізЇњзФЯжИРзЃЧж≥Х пЉЪ1гАБдЄ≠зВєзЃЧж≥ХзФЯжИРзЫізЇњпЉЫ2гАБbresenhamзЃЧж≥ХзФЯжИРзЫізЇњпЉЫ3гАБDDAзЃЧж≥Х зФЯжИРзЫізЇњгАВеЬ®ињРи°МзЪДеЃЮдЊЛз™ЧеП£дЄ≠пЉМеНХеЗївАЬзЫізЇњзФЯжИРзЃЧж≥ХвАЭиПЬеНХпЉМеПѓйАЪињЗеЉєеЗЇзЪДиПЬеНХпЉМйАЙжЛ©дЄНеРМзЪД...
### DDAзЫізЇњзФЯжИРзЃЧж≥Х #### дЄАгАБзЃАдїЛ еЬ®иЃ°зЃЧжЬЇеی嚥е≠¶дЄ≠пЉМDDAпЉИDigital Differential AnalyzerпЉМжХ∞е≠ЧеЈЃеИЖеИЖжЮРеЩ®пЉЙзЃЧж≥ХжШѓдЄАзІНзФ®дЇОзїШеИґзЫізЇњзЪДеЯЇжЬђзЃЧж≥ХгАВеЃГйАЪињЗиЃ°зЃЧжѓПдЄАж≠•зІїеК®зЪДжЦєеРСжЭ•йАЉињСзРЖжГ≥зЫізЇњзЪДдљНзљЃпЉМдїОиАМеЃЮзО∞зЫізЇњ...
дЄЛйЭҐе∞Жиѓ¶зїЖиЃ®иЃЇеЗ†зІНеЄЄиІБзЪДзЫізЇњзФЯжИРзЃЧж≥ХгАВ 1. **жЙЂжППзЇњзЃЧж≥Х**пЉЪ жЙЂжППзЇњзЃЧж≥ХжШѓдЄАзІНеЯЇжЬђзЪДдЇМзїіеی嚥зїШеИґжЦєж≥ХпЉМйАВзФ®дЇОе±ПеєХжШѓзФ±дЄАз≥їеИЧж∞іеє≥и°МеГПзі†зїДжИРзЪДеЬЇжЩѓгАВиѓ•зЃЧж≥ХдїОе±ПеєХзЪДй°ґйГ®еИ∞еЇХйГ®йАРи°МжЙЂжППпЉМж£АжЯ•жѓПжЭ°зЫізЇњжШѓеР¶дЄОељУеЙН...
02DDAпЉЪзЫізЇњзЪДDDAзФЯжИРзЃЧж≥Х 03MidPaintпЉЪзЫізЇњдЄ≠зВєзФЯжИРзЃЧж≥Х 04BresenhamпЉЪзЫізЇњBresenhamзФЯжИРзЃЧж≥Х 05DrawCircleпЉЪдЄ≠зВєзФїеЬЖзЃЧж≥Х 06DrawEllipseпЉЪдЄ≠зВєзФїж§≠еЬЖзЃЧж≥Х 07EdgeTablePolygonпЉЪе§Ъ茺嚥жЬЙеЇПиЊєи°®зЃЧж≥Х 08пЉЪиЊєж†ЗењЧ...
еЬ®иЃ°зЃЧжЬЇеی嚥е≠¶дЄ≠пЉМзЫізЇњжЃµзЪДзФЯжИРзЃЧж≥ХжШѓеЯЇз°АдЄФйЗНи¶БзЪДзїДжИРйГ®еИЖгАВињЩдЇЫзЃЧж≥ХдљњеЊЧиЃ°зЃЧжЬЇиГље§ЯйЂШжХИеЬ∞еЬ®е±ПеєХдЄКзїШеИґеЗЇеє≥жїСзЪДзЇњжЭ°гАВдї•дЄЛжШѓдЄЙзІНеЄЄиІБзЪДзЫізЇњзФїж≥ХпЉЪDDAзЃЧж≥ХгАБдЄ≠зВєзФїзЇњзЃЧж≥Хдї•еПКBresenhamзЃЧж≥ХгАВ 1. DDAпЉИDigital ...
еЕґдЄ≠пЉМжХ∞е≠ЧеЊЃеИЖеИЖжЮРеЩ®пЉИDigital Differential AnalyzerпЉМзЃАзІ∞DDAпЉЙзЃЧж≥ХжШѓдЄАзІНеЄЄзФ®зЪДзЇњжАІжПТеАЉжЦєж≥ХпЉМзФ®дЇОзФЯжИРзЫізЇњдЄКзЪДеГПзі†зВєгАВжЬђжЦЗе∞ЖжЈ±еЕ•жОҐиЃ®DDAзЃЧж≥ХзЪДеЈ•дљЬеОЯзРЖеПКеЕґеЬ®еЃЮйЩЕзЉЦз®ЛдЄ≠зЪДеЇФзФ®гАВ ### DDAзЃЧж≥ХеОЯзРЖ DDAзЃЧж≥ХзЪД...
йАЙеЃЪдЄАзІНеЯЇжЬђеی嚥пЉИзЫізЇњжЃµпЉЙпЉМзЉЦеЖЩзФЯжИРиѓ•еЯЇжЬђеی嚥зЪДжЇРз®ЛеЇПпЉМеєґиГљеЬ®иЃ°зЃЧжЬЇдЄКзЉЦиѓСињРи°МпЉМзФїеЗЇж≠£з°ЃзЪДеی嚥
иЃ°зЃЧжЬЇеی嚥е≠¶ зЫізЇњDDAзЃЧж≥ХиЃ°зЃЧжЬЇеی嚥е≠¶ зЫізЇњDDAзЃЧж≥ХиЃ°зЃЧжЬЇеی嚥е≠¶ зЫізЇњDDAзЃЧж≥ХиЃ°зЃЧжЬЇеی嚥е≠¶ зЫізЇњDDAзЃЧж≥ХиЃ°зЃЧжЬЇеی嚥е≠¶ зЫізЇњDDAзЃЧж≥ХиЃ°зЃЧжЬЇеی嚥е≠¶ зЫізЇњDDAзЃЧж≥ХиЃ°зЃЧжЬЇеی嚥е≠¶ зЫізЇњDDAзЃЧж≥ХиЃ°зЃЧжЬЇеی嚥е≠¶ зЫізЇњDDAзЃЧж≥ХиЃ°зЃЧжЬЇ...
еЬ®иЃ°зЃЧжЬЇеی嚥е≠¶йҐЖеЯЯпЉМзЫізЇњзФЯжИРзЃЧж≥ХжШѓиЗ≥еЕ≥йЗНи¶БзЪДеЯЇз°АйГ®еИЖпЉМзЙєеИЂжШѓеЬ®дљњзФ®зЉЦз®Лиѓ≠и®Ае¶ВVBпЉИVisual BasicпЉЙињЫи°Меی嚥зїШеИґжЧґгАВзЫізЇњзФЯжИРзЃЧж≥ХеЕБиЃЄжИСдїђйАЪињЗдї£з†БеЬ®е±ПеєХдЄКз≤Њз°ЃеЬ∞жППзїШеЗЇзЫізЇњпЉМињЩжШѓжЮДеїЇжЫіе§НжЭВзЪДеی嚥еТМеЫЊеГПзЪДеЯЇз°АгАВ...