以下是刚刚完成的一个作业,后半部分图文互换太麻烦了,我都贴了图,会有一些不齐,凑合看吧,3个实验的代码比较长,欢迎来信索取文档和3份代码,我的email:mgigabyte[艾特]gmail.com
可能会有部分网友感觉很垃圾,很无聊,权且仅当是一个作业吧,我对这个作业的预算是3天,实际1天半完成,还是比较满意的。
字典序全排列生成算法提速
摘 要: 本文实验了字典序全排列生成算法,并给出了三种优化方法,采用t假设检验的方法证明3种优化方法都可接受,最终的优化方法比作为baseline的算法提速了29.7倍。
关键词:字典序全排列生成算法;t假设检验。
1 引言
在全排列生成方法是一种将n个不同的项按照一定的顺序,无重复、无遗漏地列举出全部的不同的排列方法,n个不同项将会生成n阶层个不同的排列方案,在这些方法中字典序方法最为自然容易理解,但字典序法不可避免地需要循环或者递归,而以邻位对换法等为代表的LOOPLESS的方法避免了循环和递归,但由于每次执行都需要依赖此前的结果,因此在分布式,多核环境下显得性能不高。字典序方法虽然依赖循环和递归但其很容易将任务分解在不同的计算单元在多核,甚至是分布式的环境下,可以获得很好的性能。本文从字典序的3重优化过程,来探讨字典序的性能提速。
2 相关工作
论文[1]提到了常见的通过邻位对换法来获得全排列生成算法,论文[2]讨论了并行计算排列生成算法,并且支持scalability,性能和计算机CPU核数量相关,论文[3]提出了一种新的计算第kth个排列方案的并行算法。
3 系统的优化方法
本文利用字典序的基本算法,生成一个最简单的算法作为性能比较的baseline。之后采用了递归底部消除,多线程,文件读写优化等方法,将性能提升29.7倍。
以[1,2,3,4]为例进行举例:
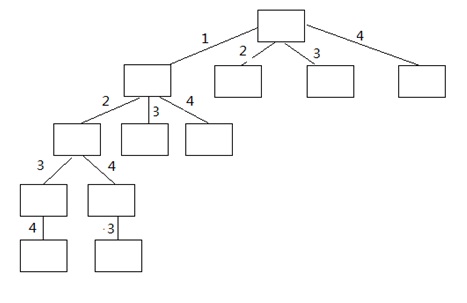
图1 递归过程
递归过程为一个从k叉树逐级递减,直到1叉树,深入优先的过程,栈的深度为O(n),n为给出的n不同项的数目。
第一个优化的想法:在递归到某个k叉树的节点时,没有必要继续递归,而是可以直接求解,从而消除底部的递归,实验尝试了消除底部1层的递归,消除2层的递归和消除3层的递归,实验表明消除2层的递归的性能更加优良,性能提升3%,并以此为基础继续进行优化。
第二个优化的想法:整个计算都是顺序执行,系统的其他CPU核并没有使用上,使用并行计算的方法对计算资源进行饱和。和第一种优化思路相反,本文使用了在递归树的顶部进行展开出9个线程分别计算,实验表明采用这种方法,性能提升31%,如图2所示。
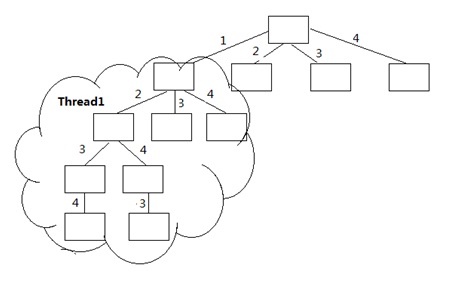
图2 多线程方法等价于在顶部展开
如图2所示,1打头的字典序算法由一个独立的线程完成,并写入一个独立的文件f1。因此4个元素的情况下,结果会生成4个文件,最后用cat命令将这4个文件进行合并输出。如果将结果输出文件看成一个织布,那么这里同时让4个织布工人同时织布,每个织布工人都从头开始织布,不考虑其他织布工人的情况,最后把各自的织布合并成为一个完成的布匹。
第三个优化方法是:从结果文件的角度考虑系统同时有10个线程在进行磁盘IO,最后还需要进行一次合并,如果采用mmap将文件映射到内存,直接在内存中写入,最后一次性sync进磁盘,可以大大提高效率。实验表明采用这种方法后,性能提升2183%。只所以能高效优化,可以认为4个织布工人在同一张大布上分别织布,织完后就是最后的结果,不同的工人织布的起始点不同,各自安排好织布的起始点分别织布。性能的提升主要和mmap这种文件读写加速有关。
使用最优的优化算法后,我们对9个不同的项做了实验,在最好的算法下,9阶层个输出项只需要平均0.042秒即可完成,相当于输出一个项只需0.12微秒。
4 实验和分析
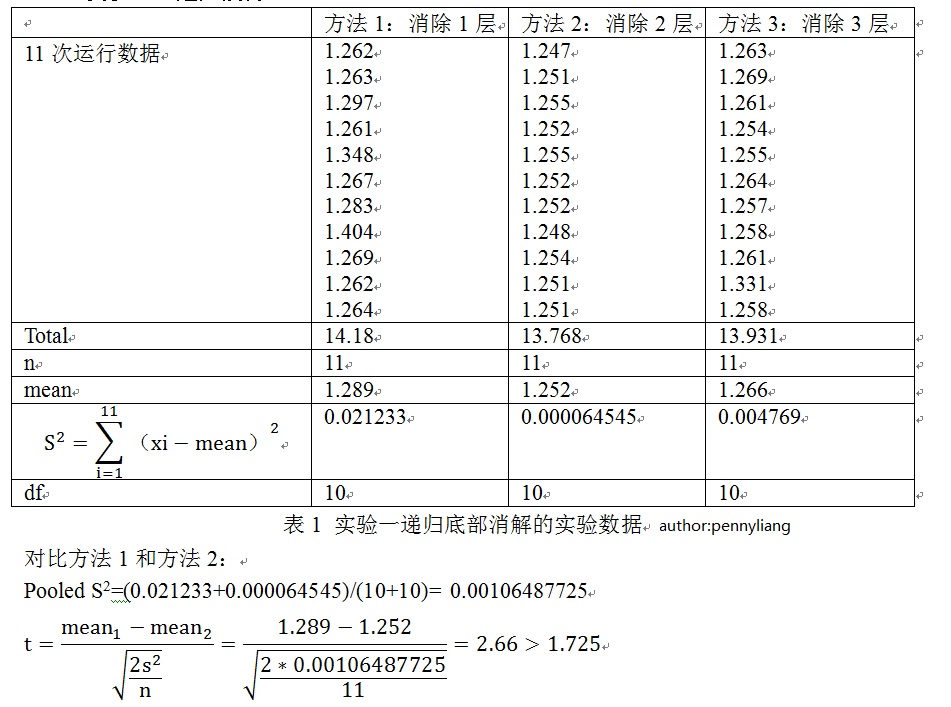
首先我们使用了递归底部展开的优化方法,该优化方法与快速排序在递归到最后k个元素后采用简单的直接插入排序类似,以下是实验一的数据,我们采用t检验的假设检验的方法,这种方法可以有效地估计性能提升是否可以接受。用t检验来对3种展开的方法进行效果估计,并在最后给出了产生这些数据的分析。
实验结论,方法2比方法1和方法3都具有显著的性能提升,方法2的有效性可以接受。
4.1 实验一 递归展开


分享到:
















相关推荐
全排列生成算法是一种在...总结来说,"全排列生成算法字典序vc++源码"涉及了计算机科学中的经典算法问题,包括全排列生成、字典序排列以及C++编程实践。理解并实现这样的算法对于提升编程能力和解决实际问题至关重要。
排列生成算法是计算机科学中处理有限集合的一种方法,主要用于生成所有可能的排列顺序。这里主要讨论两种算法:字典序法和邻位互换法。 字典序法是一种按照特定顺序(通常是最小字典序)生成排列的算法。在字典序中...
N个数字的字典序全排列,自己的小作业,参考dfs写的,
组合数学中的全排列生成算法是解决数学问题和编程挑战中不可或缺的部分,特别是在处理组合和排列问题时。全排列指的是从n个不同元素中取出n个元素的所有可能排列方式。在这个问题中,我们将探讨六种常用的全排列生成...
全排列生成算法是计算机科学中一个经典的问题,主要应用于数据处理、组合优化等领域。本话题主要探讨了四种不同的方法:字典序排列、邻位对换、递增进位制数和递减进位制数,并提供了C++语言的实现。 1. **字典序...
利用中介数实现全排列算法,采用java实现。
使用递归 :-------------输入给出正整数n,输出1到n的全排列,排列的输出顺序为字典序,每种排列占一行,数字间无空格,
本项目提供了C语言实现的四种常见全排列生成算法,分别是字典序法、循环左移、循环右移以及邻位对换方法。 1. **字典序法**: 字典序法是一种按照特定顺序(通常是最小到最大)生成排列的方法。在C语言中,可以...
全排列的生成算法 全排列的生成算法是指对于给定的字符集,用有效的方法将所有可能的全排列无重复无遗漏地枚举出来。任何 n 个字符集的排列都可以与 1~n 的 n 个数字的排列一一对应,因此在此就以 n 个数字的排列...
本篇文章将详细介绍几种常见的全排列生成算法,包括字典序法、递增进位数制法、递减进位数制法、邻位交换法、n进位制法以及递归类算法。通过这些方法,可以高效地生成给定字符集的所有可能排列。 #### 二、字典序法...
本文件主要介绍了四种权威的全排列生成算法,分别是字典序(基于中介数)算法、字典序(基于相邻排列特征)算法、递增进位制数法和递减进位制数法。这些算法可以帮助程序员有效地生成一个给定数组的所有可能全排列,...
在C语言中实现字典序全排列,需要对算法有深入的理解,通常会用到递归或回溯等技术。 字典序全排列的实现方法: 1. **回溯法**:回溯法是一种试探性的解决问题的方法,当遇到无效解或找到有效解时,能够退回之前的...
字典序法是按照字典顺序生成全排列的一种方法。它首先将所有元素按照字典顺序排列,然后逐个尝试每个位置上的下一个元素,如果当前元素已经是最大值,则尝试下一个位置。在尝试过程中,如果发现无法找到下一个更大的...
本篇文章将详细介绍四种权威全排列生成算法,包括基于中介数、相邻排列特征、递增进位制数法和递减进位制数法的方法。 1. 基于中介数的全排列算法: 这种方法通常用于生成字典序排列。在`Zidian1_1`和`Zidian1_2`...
字典序法生成全排列,希望对学习组合数学的同学有帮助
总之,字典排序求全排列的算法通过Java实现,结合了回溯法和深度优先搜索策略,遵循字典序规则生成所有可能的排列。理解并掌握这种算法有助于提升编程能力和解决复杂问题的能力。在实际应用中,这种算法可用于生成...
排列生成算法 字典序法 C语言源代码 排列生成算法的一种,采用交换和逆序的方法生成排列
组合数学全排列字典序法组合数学全排列字典序法组合数学全排列字典序法组合数学全排列字典序法组合数学全排列字典序法组合数学全排列字典序法组合数学全排列字典序法组合数学全排列字典序法
以上内容涵盖了全排列算法的多个重要方面,包括基本定义、时间复杂度分析、算法设计、递归方法、字典序排列、STL函数使用、中介数概念、进位制方法、邻位对换法以及组合数生成等。这些知识点对于理解全排列算法的...
以下是一个基于深度优先搜索(DFS)的字典序排列生成算法的基本思路: 1. 为每个元素创建一个标记数组,用于记录当前元素是否已被使用过。 2. 定义一个递归函数,该函数接受当前排列的数组和剩余未使用元素的计数。...