Kaplan-Meier estimator(From Wikipedia, the free encyclopedia)

Kaplan-Meier estimator

From Wikipedia, the free encyclopedia

Jump to: navigation, search

<!-- start content -->

This article does not cite any references or sources. Please help improve this article by adding citations to reliable sources (ideally, using inline citations). Unsourced material may be challenged and removed. (April 2009)

The Kaplan-Meier estimator (also known as the product limit estimator) estimates the survival function from life-time data. In medical research, it might be used to measure the fraction of patients living for a certain amount of time after treatment. An economist might measure the length of time people remain unemployed after a job loss. An engineer might measure the time until failure of machine parts.

A plot of the Kaplan-Meier estimate of the survival function is a series of horizontal steps of declining magnitude which, when a large enough sample is taken, approaches the true survival function for that population. The value of the survival function between successive distinct sampled observations ("clicks") is assumed to be constant.

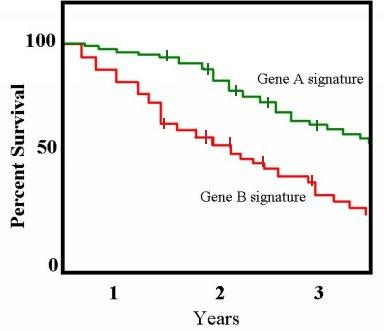
An example of a Kaplan-Meier plot for two conditions associated with patient survival

An important advantage of the Kaplan-Meier curve is that the method can take into account "censored" data — losses from the sample before the final outcome is observed (for instance, if a patient withdraws from a study). On the plot, small vertical tick-marks indicate losses, where patient data has been censored. When no truncation or censoring occurs, the Kaplan-Meier curve is equivalent to the empirical distribution.

In medical statistics, a typical application might involve grouping patients into categories, for instance, those with Gene A profile and those with Gene B profile. In the graph, patients with Gene B die much more quickly than those with gene A. After two years about 80% of the Gene A patients still survive, but less than half of patients with Gene B.

[edit] Formulation

Let S(t) be the probability that an item from a given population will have a lifetime exceeding t. For a sample from this population of size N let the observed times until death of N sample members be

Corresponding to each t_i is n_i, the number "at risk" just prior to time t_i, and d_i, the number of deaths at time t_i.

Note that the intervals between each time typically will not be uniform. For example, a small data set might begin with 10 cases, have a death at Day 3, a loss (censored case) at Day 9, and another death at Day 11. Then we have (t₁ = 3,t₂ = 11), (n₁ = 10,n₂ = 8), and (d₁ = 1,d₂ = 1).

The Kaplan-Meier estimator is the nonparametric maximum likelihood estimate of S(t). It is a product of the form

When there is no censoring, n_i is just the number of survivors just prior to time t_i. With censoring, n_i is the number of survivors less the number of losses (censored cases). It is only those surviving cases that are still being observed (have not yet been censored) that are "at risk" of an (observed) death.

There is an alternate definition that is sometimes used, namely

The two definitions differ only at the observed event times. The latter definition is right-continuous whereas the former definition is left-continuous.

Let T be the random variable that measures the time of failure and let F(t) be its cumulative distribution function. Note that

Consequently, the right-continuous definition of may be preferred in order to make the estimate compatible with a right-continuous estimate of F(t).

[edit] Statistical considerations

The Kaplan-Meier estimator is a statistic, and several estimators are used to approximate its variance. One of the most common such estimators is Greenwood's formula:

In some cases, one may wish to compare different Kaplan-Meier curves. This may be done by several methods including:

• The log rank test
• The Cox proportional hazards test

<!-- NewPP limit report Preprocessor node count: 216/1000000 Post-expand include size: 3500/2048000 bytes Template argument size: 1218/2048000 bytes Expensive parser function count: 1/500 --><!-- Saved in parser cache with key enwiki:pcache:idhash:3168650-0!1!0!default!!en!2 and timestamp 20090406062601 -->

Retrieved from "http://en.wikipedia.org/wiki/Kaplan-Meier_estimator"

Hidden categories: Articles lacking sources from April 2009 | All articles lacking sources

<!-- end content -->