求点集中的最近点对有以下两种方法:
设p1=(x1, y1), p2=(x2, y2), …, pn=(xn, yn)是平面上n个点构成的集合S,设计算法找出集合S中距离最近的点对。
1、蛮力法(适用于点的数目比较小的情况下)
1)算法描述:已知集合S中有n个点,一共可以组成n(n-1)/2对点对,蛮力法就是对这n(n-1)/2对点对逐对进行距离计算,通过循环求得点集中的最近点对:
2)代码描述:
double MinDistance = double.maxvalue; //设置一个MinDistance存储最近点对的距离,初始值为无穷大
int PointIndex1,PointIndex2; //设置PointIndex1,PointIndex2分别存储最近点对的两个点编号
for (i=1; i< n; i++) //循环计算n(n-1)/2对点对的距离
{
for (j=i+1; j<=n; j++)
{
double PointDistance = Distance(S[i],S[j]); //求得point i和point j之间的距离
if PointDistance < MinDistance; //如果当前点对距离小于最小点对距离,则设置最小点对距离等于当前点对距离
{
MinDistance = PointDistance;
PointIndex1 = i;
PointIndex2 = j;
}
}
}
3)算法时间复杂度:算法一共要执行 n(n-1)/2次循环,因此算法复杂度为O(n2)
2、分治法
1)算法描述:已知集合S中有n个点,分治法的思想就是将S进行拆分,分为2部分求最近点对。算法每次选择一条垂线L,将S拆分左右两部分为SL和SR,L一般取点集S中所有点的中间点的x坐标来划分,这样可以保证SL和SR中的点数目各为n/2,
(否则以其他方式划分S,有可能导致SL和SR中点数目一个为1,一个为n-1,不利于算法效率,要尽量保持树的平衡性)
依次找出这两部分中的最小点对距离:δL和δR,记SL和SR中最小点对距离δ
= min(δL,δR),如图1:
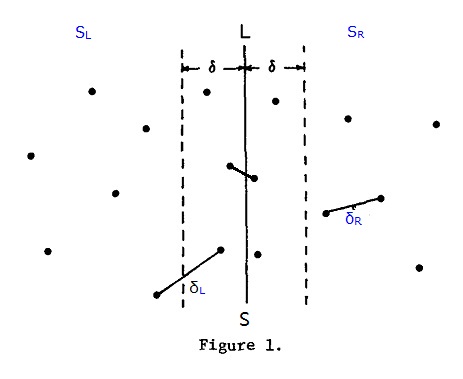
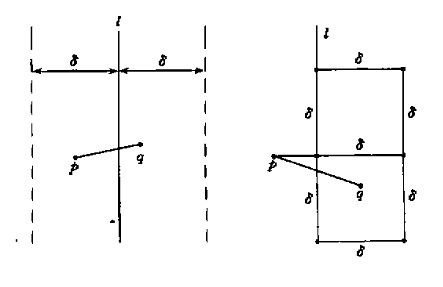
以L为中心,δ为半径划分一个长带,最小点对还有可能存在于SL和SR的交界处,如下图2左图中的虚线带,p点和q点分别位于SL和SR的虚线范围内,在这个范围内,p点和q点之间的距离才会小于δ,最小点对计算才有意义。
Figure 2
对于SL虚框范围内的p点,在SR虚框中与p点距离小于δ的顶多只有六个点,就是图二右图中的2个正方形的6的顶点。这个可以反推证明,如果右边这2个正方形内有7个点与p点距离小于δ,例如q点,则q点与下面正方形的四个顶点距离小于δ,则和δ为SL和SR中的最小点对距离相矛盾。因此对于SL虚框中的p点,不需求出p点和右边虚线框内所有点距离,只需计算SR中与p点y坐标距离最近的6个点,就可以求出最近点对,节省了比较次数。
(否则的话,最坏情形下,在SR虚框中有可能会有n/2个点,对于SL虚框中的p点,每次要比较n/2次,浪费了算法的效率)
代码描述:
1)对点集S的点x坐标和y坐标进行升序排序,获得点集Sx和Sy
2)令δ=∞;
//δ为最小点位距离
3)Divide_conquer(Sx,Sy,δ)
//分治法
if (Sx.count=1) then
δ=∞;
//如果Sx中只有一个点,则δ=∞
return
δ;
else if(Sx.count=2 and d(Sx.[0],Sx.[1])<δ)
//如果Sx中只有2个点,则δ为两点之间距离
δ=d(Sx.[0],)Sx.[1]);
return
δ;
else
//如果Sx中多于2个点,则将Sx,Sy分治,以中心点画线,将Sx分为左右两部分SxL和SxR,Sy分为SyL和SyR
j1=1,j2=1,k1=1,k2=1;
mid =
Sx.count/2; //mid为Sx中的中间点点号
L =
Sx.[mid].x;
//L为Sx中的中间点x坐标
for(i=1,i<Sx.count,i++)
{
if(i<=mid)
//将Sx中间线以左地方的点存入到SxL,新数组保持原来的升序性质
SxL[k1] =
Sx[i] k1++;
else
//将Sx中间线以右的地方的点存入到SxR,新数组保持原来的升序性质
SxR.count[k2] = Sx[i] k2++;
if(Sy[i].x
<L) //将Sy中间线以左地方的点存入到SyL,新数组保持原来的升序性质
SyL[j1] = Sx[i] j1++;
else
//将Sy中间线以右地方的点存入到SyR,新数组保持原来的升序性质
SyR[j2] = Sx[i] j2++;
}
δL = Divide_conquer(SxL,SyL,δ);
//获取Sx中的的最小点位距离δL
δR = Divide_conquer(SxR,SyR,δ);
//获取Sy中的的最小点位距离δR
δ= min (δL,δR);
δ=merge(SyL,SyR,δ);
//获Sx中Sy交界处的最小点位距离,并综合δL和δR
求出点集的最小点位距离δ
return
δ;
函数merge(SyL,SyR,δ)
merge(SyL,SyR,δ)
{
i1=1,i2=1;
for(i=1,i<SyL.count,i++)
//获取SyL中在左边虚框(距离小于δ)内的点,存入到S'yL中,新数组保持原来的升序性质
{
if(SyL[i].x>L-δ)
then S'yL[i1]= SyL[i], i1++,
}
for(i=1,i<SyR.count,i++)
//获取SyR中在右边虚框(距离小于δ)内的点,存入到S'yR中,新数组保持原来的升序性质
{
if(SyR[i].x<L+δ)
then S'yR[i2]= SyR[i], i2++,
}
t=1;
for(i=1,i<S'yL.count,i++)
{
while(S'yR[t].y< S'yL[t].yand t < SyR.count)
//获取点集S'yR内距离点S'yL[t]y坐标最接近的点号
{ t++; }
for( j= max(1,t-3), j<=min(t+3,S'yR.count),j++) //计算S'yR中的点与S'yL[t]y坐标相邻的六个点的距离
{
if(d(S'yL[i],S'yL[j])<δ)
//如果前两点之间距离小于δ
then δ = d(S'yL[i],S'yL[j]);
//则最小点位距离δ为当前两点之间距离
}
return δ
}
3)算法时间复杂度:
首先对点集S的点x坐标和y坐标进行升序排序,需要循环2nlogn次,复杂度为O(2nlogn)
接下来在分治过程中,对于每个S'yL中的点,都需要与S'yR中的6个点进行比较
O(n)= 2O(n/2) + (n/2)*6(一个点集划分为左右两个点集,时间复杂度为左右两个点集加上中间区域运算之和)
其解为O(n)< O(3nlogn)
因此总的时间复杂度为O(3nlogn),比蛮力法的O(n2)要高效。
分享到:










相关推荐
在计算机科学领域,解决平面上n个点之间最近点对问题是一个经典的算法问题。这个问题的目标是找到一组给定点中距离最近的两个点。这在地理信息系统、数据挖掘和图形学等领域有着广泛的应用。本问题可以通过多种算法...
### 分治法求最近点对问题 #### 实验目的与内容概述 本次实验的主要目标是理解和实现分治法解决最近点对问题。具体任务包括: 1. **最近点对问题**:给定平面上的N个点,找到其中两点间的最小距离。 2. **随机...
平面最近点对问题分治算法解答,C++实现,代码整洁规范。
1. 对于平面上给定的N个点,给出所有点对的最短距离,即,输入是平面上的N个点,输出是N点中具有最短距离的两点。2. 要求随机生成N个点的平面坐标,应用蛮力法编程计算出所有点对的最短距离。3. 要求随机生成N个点的...
在计算机科学领域,寻找平面上最近点对是一个经典的空间数据结构问题,特别是在大规模数据处理中。这个题目描述的是一个使用C语言实现的算法,能够处理多达2亿个点的情况。这个算法的目标是找出平面上所有点对中距离...
1. **问题描述**:理解平面最近点问题的具体背景与意义。 2. **算法设计思想**:掌握分治法解决问题的基本思路。 3. **程序设计**:学会使用C++编程语言实现分治法求解平面最近点问题。 4. **复杂性分析**:能够对...
【平面最接近点对问题】是指在平面上给定n个点,寻找其中距离最近的两点。这是一个经典的计算几何问题,对于大规模数据处理时,直接的暴力求解方法(检查所有点对)效率低下。 **分治算法**是解决此类问题的一种...
**标题解析:**“分治法求最近点对”指的是使用分治策略来解决寻找二维空间中距离最近的两个点的问题。在计算机科学中,分治法是一种将复杂问题分解成更小、易于处理的部分的方法,然后分别解决这些部分,最后合并...
在计算机科学中,"求平面上最接近点对算法实现"是一个经典的几何问题,它涉及到数据结构、算法设计以及计算几何。这个问题的目标是找到给定的一组二维坐标点中,距离最近的两个点对。这样的算法在多个领域都有应用,...
实验进行的是求二维空间内最近点对的算法,使用c++进行实现,测试环境是CLION。
这个问题要求在给定的二维平面上的一组点中,找到距离最近的两个点。这个问题广泛应用于各种场景,如数据挖掘、图形学、地理信息系统等,因为它涉及到寻找数据之间的最小距离或最近邻的问题。 递归与分治是解决此类...
总结起来,修正的分治法在求解最近点对问题时,通过有序划分和有效剪枝,大大降低了搜索的复杂度,尤其在大数据集上表现出较高的效率。这种方法不仅体现了分治法的思想,也展示了如何通过算法设计的创新来优化问题的...
在“平面最接近点对问题”中,我们的目标是找到一组二维平面上的点对,使得它们之间的距离最小。 平面最接近点对问题可以这样描述:给定n个位于二维平面上的点,找出其中任意两点之间的最小距离。这是一个经典的...
不会吧!都2022年了,你还没有弄懂最接近点...4)在二维情形下如何能用线性时间完成左右最近点对与中间跨分割线点对的比较? 5)对算法做时间复杂性分析。 6)本题选做:二维情形设采用分治法解最接近点对问题,编程实现。
平面最近点对问题指的是在一个二维平面上给定n个点,找出其中距离最近的两个点。直观上,这个问题可以通过比较所有点对之间的距离来解决,但随着点的数量增加,这种全排列的暴力求解方法时间复杂度高达O(n^2),对于...
1. 对于平面上给定的N个点,给出所有点对的最短距离,即,输入是平面上的N个点,输出是N点中具有最短距离的两点。2. 要求随机生成N个点的平面坐标,应用蛮力法编程计算出所有点对的最短距离。3. 要求随机生成N个点的...
使用java编写 用分治法实现对于平面上最近点对的查找 使用Swing作为界面
最近点对问题是指在一个二维平面上,给定n个点,寻找其中距离最近的两个点。这是一个经典的计算几何问题,有多种解决方案,其中之一就是利用分治算法。下面,我们将深入探讨这个问题以及C++实现的细节。 首先,我们...
给出平面上的 N 个二维点,求出距离最小的 2 个点对。本题中距离定义为他们的直线距离。例如(0,0) (3,4)的距离为 5. ★数据输入: 有多组数据,对于每组数据,第一行是一个数字 N 表示点的个数。N=0 的时候说明输入...
在求平面最近对的问题上,我们可以按照以下步骤进行: 1. **分解**:将点集分为两半,递归地求解左半部分和右半部分的最近对。 2. **解决**:在每个子集内部寻找最近对,这个过程可以通过比较所有点对之间的距离来...