摘取自维基百科:
http://zh.wikipedia.org/wiki/%E6%95%B0%E5%AD%A6%E5%BD%92%E7%BA%B3%E6%B3%95
数学归纳法(Mathematical Induction,通常简称为MI)是一种数学证明方法,通常被用于证明某个给定命题在整个(或者局部)自然数范围内成立。虽然数学归纳法名字中有“归纳”,但是数学归纳法并不是不严谨的归纳推理法,它是属于完全严谨的演绎推理法。
定义
最简单和常见的数学归纳法是证明当 n 等于任意一个自然数时某命题成立。证明分下面两步:
- 证明当 n = 1 时命题成立。
- 证明如果在 n = m 时命题成立,那么可以推导出在 n = m+1 时命题也成立。(m 代表任意自然数)
这种方法的原理在于:首先证明在某个起点值时命题成立,然后证明从一个值到下一个值的过程有效。当这两点都已经证明,那么任意值都可以通过反复使用这个方法推导出来。把这个方法想成多米诺效应也许更容易理解一些。例如:你有一列很长的直立着的多米诺骨牌,如果你可以:
- 证明第一张骨牌会倒。
- 证明只要任意一张骨牌倒了,那么与其相邻的下一张骨牌也会倒。
那么便可以下结论:所有的骨牌都会倒。
例子
假设我们要证明下面这个公式(命题):

其中 n 为任意自然数。这是用于计算前 n 个自然数的和的简单公式。证明这个公式成立的步骤如下。
第一步
第一步是验证这个公式在 n = 1 时成立。我们有左边 = 1,而右边 = 1(1 + 1) / 2 = 1,所以这个公式在 n = 1 时成立。第一步完成。
第二步
我们先假设 n = m 时公式成立。即
 (等式 1)
(等式 1)
然后在等式等号两边分别加上 m + 1 得到
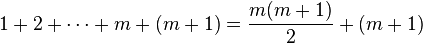 (等式 2)
(等式 2)
这就是 n = m+1 时的等式。我们现在需要根据等式 1 证明等式 2 成立。通过因式分解合并,等式 2 的右手边
![= \frac{m(m + 1)}{2} + \frac{2(m + 1)}{2}
= \frac{(m + 2)(m + 1)}{2}
= \frac{(m + 1)(m + 2)}{2}
= \frac{(m + 1)[(m + 1) + 1]}{2}.](http://upload.wikimedia.org/math/3/8/e/38eb7d58dad30505091f7aa911bc1c3d.png)
也就是说
![1 + 2 + \cdots + (m + 1) = \frac{(m + 1)[(m + 1) + 1]}{2}](http://upload.wikimedia.org/math/8/e/1/8e121ee42835ec53a1c0346c07d5d003.png)
这样便证明了从 P(m) 成立可以推导出 P(m+1) 也成立。证明至此结丛,结论:对于任意自然数 n,P(n) 均成立。
解释
在这个证明中,归纳推理的过程如下:
- 首先证明 P(1) 成立,即公式在 n = 1 时成立。
- 然后证明从 P(m) 成立可以推导出 P(m+1) 也成立。(这里实际应用的是演绎推理法)
- 根据上两条从 P(1) 成立可以推导出 P(1+1),也就是 P(2) 成立。
- 继续推导,可以知道 P(3)成立。
- 从 P(3) 成立可以推导出 P(4) 也成立。
- 不断重复推导下一命题成立的步骤。(这就是所谓“归纳”推理的地方)
- 我们便可以下结论:对于任意自然数 n,P(n) 成立。






相关推荐
《重温基于图的协同过滤:一种线性残差图卷积网络方法》是AAAI2020年提出的一种创新的推荐系统模型。该模型利用了图卷积网络(Graph Convolutional Network, GCN)的技术,针对传统协同过滤算法的不足进行了优化,...
### Python中的XML工具详解 #### 一、引言 随着互联网的发展,XML(可扩展标记语言)作为一种重要的数据交换格式,在各种系统间的数据传输中扮演着至关重要的角色。Python作为一种强大的脚本语言,具备出色的文本...
这些游戏以其独特的游戏设计、丰富的关卡内容和新颖的玩法,深受当时的玩家喜爱。 从技术角度来看,这款模拟器的便捷性和用户友好性也是一大亮点。它的绿色安全特性确保了用户下载和使用的安全性,不必担心病毒或...
此外,书中还对一些重要的数学和物理学问题进行了详细的阐述,这些内容超出了传统微积分的范畴,涉及实分析、复分析、偏微分方程、泛函分析、变分法和拓扑学等数学分支。 齐民友在书中提出了三个写作目的。首先是...
但凡事大都有主要矛盾,学数学分析也应该抓主要思想。根据笔者这些年对 数学分析的体会,感觉有三大基本思想是数学分析的核心,逼近、变换和分解。 围绕微分、积分和级数这三大主题,展开上述三大基本思想,构成了...
《重温微积分》是齐民友教授所著的一部关于微积分及其相关数学领域的深入探讨书籍。该书不仅涵盖微积分的传统内容,还深入探讨了微积分在现代数学中的应用和相关领域的发展。在知识点方面,该书从多个维度对微积分...
除了上述章节外,《重温微积分》还特别强调了数学与物理学之间的内在联系。书中通过具体实例展示了微积分及其相关理论在经典力学、电磁学等物理学科中的应用。这种跨学科的视角有助于培养读者的综合思维能力。 ####...
综上所述,"高等数学课件ppt 高等数学上册"是一份全面、实用的学习资料,无论你是初次接触还是重温高等数学,都能从中受益匪浅。通过深入学习和理解这些内容,你将能够更好地掌握这门学科,并为后续的专业学习打下...
重温微积分 - 齐民友
成人高考数学复习是一项至关重要的任务,旨在帮助学生们重温并强化中学阶段的数学基础知识,提升其数学思维能力。这其中包括空间想象能力、直觉猜想、归纳抽象、符号表示、运算求解、演绎证明以及体系构建等多方面的...
而在几何学的应用中,微积分同样功不可没,比如在计算曲线的弧长、曲面的面积和体积时,积分法提供了精确的解决方案。 随着数学的发展,微积分理论也在不断完善。从早期的无穷小分析到黎曼积分、勒贝格积分,再到...
总的来说,《考研数学公式WORD版》是一份系统全面、内容丰富的数学公式手册,无论对于考研学生还是需要重温数学概念的工程师来说,它都是一份宝贵的资源,有助于读者在数学学习和研究的道路上更加自信和从容。...
考研数学一是全国硕士研究生入学考试中的一个重要科目,主要考察考生的数学基础知识、逻辑推理能力和问题解决能力。这个压缩包文件“考研数学一历年真题和答案”包含了自1995年以来的所有考研数学一真题及其详细的...
选择题部分通过多样化的问题设计,让学生们在实践中重温比例、百分比、几何图形、分数运算等核心概念。第1题的降价问题,要求学生准确地计算出降价的百分比,这不仅考查了学生的计算能力,还能够培养他们对经济活动...
小学数学复习课是教学过程中的重要环节,旨在巩固学生的基础知识,提高他们的综合能力。本文将探讨如何上好小学数学复习课,从多个方面展开讨论。 首先,我们要明确复习课的定义。在小学数学课程中,复习课是针对一...
我们以一种符合连续有效场论(CEFT)精神的方法分析最简单的小希格斯(SLH)模型的标量势。 通过要求使用125 GeV希格斯玻色子进行正确的电弱对称破坏(EWSB),我们能够得出假轴质量mη与重顶部质量mT之间的关系,这...
标题和描述中提到的“重温俄歇效应:非弹性碰撞理论随笔”是本项研究的核心。俄歇效应(Auger Effect)是物理学中一种重要的电子激发过程,它在原子物理学、材料科学和表面分析等领域中具有广泛的应用。俄歇效应是以...
【标题】2018“华为杯”中国研究生数学建模竞赛D题是针对研究...而“第十五届‘华为杯’中国研究生数学建模竞赛—D题”这个文件很可能是当年竞赛的题目文档,对于想要了解或重温当年比赛的学者来说,是一个宝贵的资源。
什么是数学!用于数学科普、重温复习的经典著作!精心排版!公式、插图都十分精美。
同学聚会PPT模板:欢乐时光重温.pptx