本文转自:http://www.blogjava.net/zhenandaci/archive/2009/03/01/257237.html
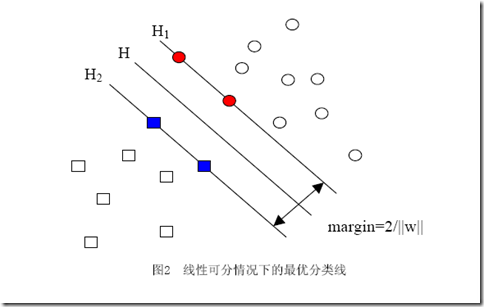
让我再一次比较完整的重复一下我们要解决的问题:我们有属于两个类别的样本点(并不限定这些点在二维空间中)若干,如图,
圆形的样本点定为正样本(连带着,我们可以把正样本所属的类叫做正类),方形的点定为负例。我们想求得这样一个线性函数(在n维空间中的线性函数):
g(x)=wx+b
使得所有属于正类的点x+代入以后有g(x+)≥1,而所有属于负类的点x-代入后有g(x-)≤-1(之所以总跟1比较,无论正一还是负一,都是因为我们固定了间隔为1,注意间隔和几何间隔的区别)。代入g(x)后的值如果在1和-1之间,我们就拒绝判断。
求这样的g(x)的过程就是求w(一个n维向量)和b(一个实数)两个参数的过程(但实际上只需要求w,求得以后找某些样本点代入就可以求得b)。因此在求g(x)的时候,w才是变量。
你肯定能看出来,一旦求出了w(也就求出了b),那么中间的直线H就知道了(因为它就是wx+b=0嘛,哈哈),那么H1和H2也就知道了(因为三者是平行的,而且相隔的距离还是||w||决定的)。那么w是谁决定的?显然是你给的样本决定的,一旦你在空间中给出了那些个样本点,三条直线的位置实际上就唯一确定了(因为我们求的是最优的那三条,当然是唯一的),我们解优化问题的过程也只不过是把这个确定了的东西算出来而已。
样本确定了w,用数学的语言描述,就是w可以表示为样本的某种组合:
w=α1x1+α2x2+…+αnxn
式子中的αi是一个一个的数(在严格的证明过程中,这些α被称为拉格朗日乘子),而xi是样本点,因而是向量,n就是总样本点的个数。为了方便描述,以下开始严格区别数字与向量的乘积和向量间的乘积,我会用α1x1表示数字和向量的乘积,而用<x1,x2>表示向量x1,x2的内积(也叫点积,注意与向量叉积的区别)。因此g(x)的表达式严格的形式应该是:
g(x)=<w,x>+b
但是上面的式子还不够好,你回头看看图中正样本和负样本的位置,想像一下,我不动所有点的位置,而只是把其中一个正样本点定为负样本点(也就是把一个点的形状从圆形变为方形),结果怎么样?三条直线都必须移动(因为对这三条直线的要求是必须把方形和圆形的点正确分开)!这说明w不仅跟样本点的位置有关,还跟样本的类别有关(也就是和样本的“标签”有关)。因此用下面这个式子表示才算完整:
w=α1y1x1+α2y2x2+…+αnynxn (式1)
其中的yi就是第i个样本的标签,它等于1或者-1。其实以上式子的那一堆拉格朗日乘子中,只有很少的一部分不等于0(不等于0才对w起决定作用),这部分不等于0的拉格朗日乘子后面所乘的样本点,其实都落在H1和H2上,也正是这部分样本(而不需要全部样本)唯一的确定了分类函数,当然,更严格的说,这些样本的一部分就可以确定,因为例如确定一条直线,只需要两个点就可以,即便有三五个都落在上面,我们也不是全都需要。这部分我们真正需要的样本点,就叫做支持(撑)向量!(名字还挺形象吧,他们“撑”起了分界线)
式子也可以用求和符号简写一下:
因此原来的g(x)表达式可以写为:
注意式子中x才是变量,也就是你要分类哪篇文档,就把该文档的向量表示代入到 x的位置,而所有的xi统统都是已知的样本。还注意到式子中只有xi和x是向量,因此一部分可以从内积符号中拿出来,得到g(x)的式子为:
发现了什么?w不见啦!从求w变成了求α。
但肯定有人会说,这并没有把原问题简化呀。嘿嘿,其实简化了,只不过在你看不见的地方,以这样的形式描述问题以后,我们的优化问题少了很大一部分不等式约束(记得这是我们解不了极值问题的万恶之源)。但是接下来先跳过线性分类器求解的部分,来看看 SVM在线性分类器上所做的重大改进——核函数。



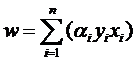
![clip_image002[4] clip_image002[4]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_1244A/clip_image002%5B4%5D_thumb.gif)
![clip_image002[6] clip_image002[6]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_1244A/clip_image002%5B6%5D_thumb.gif)



相关推荐
此外,还可以探讨在不同特征维度、数据分布等情况下,Fisher准则线性分类器的性能变化,以及与其他分类算法(如SVM、KNN等)的对比,进一步理解Fisher准则的适用性和局限性。 总之,基于Fisher准则的线性分类器设计...
线性分类器与线性支持向量机(SVM)是机器学习领域中两种重要的算法,主要用于解决二分类问题。本文将深入探讨这两种方法,并通过Matlab代码进行演示。 线性分类器是一种基于特征的简单分类模型,它通过构建一个...
在这个“线性分类器代码”压缩包中,我们很可能会找到使用Python实现的线性分类器示例,例如逻辑回归、支持向量机(SVM)或者线性判别分析(LDA)。这些模型都基于数据的线性特性进行预测,并且在诸如二分类或多元...
另一种常见的线性分类器是逻辑回归,它通过线性函数映射到概率空间,并使用sigmoid函数进行非线性变换,实现概率预测。在MATLAB中,可以使用`fisherdiscrim`函数实现LDA,或者`fitclinear`函数进行逻辑回归训练。 ...
对于线性分类器,我们通常使用梯度下降法或正规方程来求解模型参数。梯度下降是迭代方法,通过不断调整权重以最小化损失函数;正规方程则直接计算最优解,适合小规模数据集。 在numpy中,我们可以利用矩阵乘法(`@`...
非线性SVM分类器设计是支持向量机(SVM)中的一个重要研究领域。SVM是一种广泛应用于分类问题的监督学习方法。它在处理高维数据时具有良好的性能,并且对于非线性问题具有较好的处理能力。 首先,了解SVM分类器的...
通过解决优化问题,SVM可以处理线性和非线性分类任务,并且由于其优秀的泛化能力,成为机器学习中不可或缺的工具之一。在实际应用中,选择合适的核函数、调整正则化参数C以及处理大规模数据集是优化SVM模型性能的...
6. **核函数**:虽然线性SVM主要处理线性问题,但通过引入核函数,如高斯核(RBF)、多项式核、sigmoid核等,可以将数据映射到高维空间,在新的空间中实现非线性分类。 7. **正则化**:在线性SVM的优化目标中,有一...
SVM的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;SVM还包括了核技巧,这使得它成为实质上的非线性分类器。核技巧通过将原始数据映射到高维空间,使得在原空间中难以分离的数据在...
《模式识别:模型选择、SVM与分类器集成详解》 模式识别是机器学习的核心领域,涉及模型选择、分类器构建以及集成策略等多个关键概念。本文将深入探讨Adaboost算法的设计思想,模型选择的基本原则,以及SVM的理论...
### SVM入门(六)线性分类器的求解——问题的转化,直观角度 #### 1. 问题背景与目标 支持向量机(Support Vector Machine, SVM)是一种广泛应用于机器学习领域的分类与回归分析算法。本文档旨在通过一系列教程帮助...
2. SVM的核函数:讲解SVM如何处理非线性可分问题,通过引入核函数如线性核、多项式核、高斯核(RBF)等,将数据映射到高维空间,实现非线性分类。 3. 最大边界与支持向量:解释支持向量是如何定义的,它们是离决策...
在实际应用中,研究人员可以利用这些优化的SVM分类器来解决各种信号分类问题,例如声音识别、图像分类、生物医学信号分析等。通过调整参数、选择适当的核函数和优化算法,可以有效地提高模型在特定任务上的性能。
在标题“SVM.rar_gmm svm 代码_svm c代码_svm分类器_svm分类器用法”中,我们可以看到SVM与GMM(高斯混合模型)的结合,以及SVM的C语言实现和使用方法。这个压缩包文件很可能是包含了一个实现这些功能的源代码库。 ...
本文档旨在帮助读者理解支持向量机(SVM)中的线性分类器求解过程及其数学表述,特别关注于如何将线性分类器问题转化为优化问题,并讨论其解决方案。 #### 优化问题概述 在数学优化领域,一个标准的优化问题可以被...
SVM分类器中的最优化问题是指如何通过求解最优化问题来得到SVM分类器的最正确参数,使得SVM分类器的性能最好。 一、线性分类 在SVM分类器中,线性分类是指数据点在高维空间中的分类。假设我们有一个数据点ix,ix是...
非线性分类器的主要代表——神经网络和SVM,都能够通过不同的数学工具和优化策略,达到将复杂数据分类的目的。这些方法在图像识别、语音识别、自然语言处理等众多领域都有出色的表现,极大地推动了人工智能技术的...
线性分类器 - **最大间隔**:SVM试图找到一个超平面,使得正负样本距离该超平面的平均距离最大化。这种最大化间隔的方法有助于提高模型的泛化能力。 - **支持向量**:离超平面最近的样本点称为支持向量。这些点决定...
总的来说,C++实现的支持向量机SVM分类器是机器学习中的一个重要工具,结合`svm_light`库,我们可以快速构建和应用SVM模型,解决实际的分类问题。在实际项目中,开发者需要根据具体问题选择合适的参数,不断调优,以...
支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;SVM还包括核技巧,这使它成为实质上的非线性分类器。SVM的的学习...