2.9.1┬Āń«Śµ│ĢµŚČķŚ┤ÕżŹµØéÕ║”Õ«Üõ╣ē
┬Ā
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā Õ£©Ķ┐øĶĪīń«Śµ│ĢÕłåµ×ɵŚČ’╝īĶ»ŁÕÅźµĆ╗ńÜäµē¦ĶĪīµ¼ĪµĢ░T(n)µś»Õģ│õ║ÄķŚ«ķóśĶ¦äµ©ĪnńÜäÕćĮµĢ░’╝īĶ┐øĶĆīÕłåµ×ÉT(n)ķÜÅnńÜäÕÅśÕī¢µāģÕåĄÕ╣ČńĪ«Õ«ÜT(n)ńÜäµĢ░ķćÅń║¦ŃĆéń«Śµ│ĢńÜ䵌ČķŚ┤ÕżŹµØéÕ║”’╝īõ╣¤Õ░▒µś» ń«Śµ│ĢńÜ䵌ČķŚ┤ķćÅÕ║”’╝īĶ«░õĮ£’╝ÜT(n) = O(f(n))ŃĆéÕ«āĶĪ©ńż║ķÜÅķŚ«ķóśĶ¦äµ©ĪnńÜäÕó×Õż¦’╝īń«Śµ│Ģµē¦ĶĪīµŚČķŚ┤ńÜäÕó×ķĢ┐ńÄćÕÆīf(n)ńÜäÕó×ķĢ┐ńÄćńøĖÕÉī’╝īń¦░õĮ£ń«Śµ│ĢńÜäµĖÉĶ┐æµŚČķŚ┤ÕżŹµØéÕ║”’╝īń«Ćń¦░õĖ║µŚČķŚ┤ÕżŹµØéÕ║”ŃĆéÕģČõĖŁf(n)µś» ķŚ«ķóśĶ¦äµ©ĪnńÜ䵤ÉõĖ¬ÕćĮµĢ░ŃĆé
┬Ā
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā Ķ┐ÖµĀĘńö©Õż¦ÕåÖO()µØźõĮōńÄ░ń«Śµ│ĢµŚČķŚ┤ÕżŹµØéÕ║”ńÜäĶ«░µ│Ģ’╝īµłæõ╗¼ń¦░õ╣ŗõĖ║Õż¦OĶ«░µ│ĢŃĆé
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā õĖĆĶł¼µāģÕåĄõĖŗ’╝īķÜÅńØĆnńÜäÕó×Õż¦’╝īT(n)Õó×ķĢ┐µ£ĆµģóńÜäń«Śµ│ĢõĖ║µ£Ćõ╝śń«Śµ│ĢŃĆé
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā µśŠńäČ’╝īńö▒µŁżń«Śµ│ĢµŚČķŚ┤ÕżŹµØéÕ║”ńÜäÕ«Üõ╣ēÕÅ»ń¤ź’╝īµłæõ╗¼ńÜäõĖēõĖ¬µ▒éÕÆīń«Śµ│ĢńÜ䵌ČķŚ┤ÕżŹµØéÕ║”ÕłåÕł½õĖ║O(n)’╝īO(1)’╝īO(n2)ŃĆ鵳æõ╗¼ÕłåÕł½ń╗ÖÕ«āõ╗¼ÕÅ¢õ║åķØ×Õ«śµ¢╣ńÜäÕÉŹń¦░’╝īO(1)ÕŽÕĖĖµĢ░ķśČ’╝īO(n)ÕŽń║┐µĆ¦ķśČ’╝īO(n2)ÕŽÕ╣│µ¢╣ķśČ’╝īÕĮōńäČ’╝īĶ┐śµ£ēÕģČõ╗¢ńÜäõĖĆõ║øķśČ’╝īµłæõ╗¼õ╣ŗÕÉÄõ╝Üõ╗ŗń╗ŹŃĆé
┬Ā
2.9.2┬ĀµÄ©Õ»╝Õż¦OķśČµ¢╣µ│Ģ
┬Ā
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā ķéŻõ╣łÕ”éõĮĢÕłåµ×ÉõĖĆõĖ¬ń«Śµ│ĢńÜ䵌ČķŚ┤ÕżŹµØéÕ║”Õæó’╝¤ÕŹ│Õ”éõĮĢµÄ©Õ»╝Õż¦OķśČÕæó’╝¤µłæõ╗¼ń╗ÖÕć║õ║åõĖŗķØóńÜäµÄ©Õ»╝µ¢╣µ│Ģ’╝īÕ¤║µ£¼õĖŖ’╝īĶ┐Öõ╣¤Õ░▒µś»µĆ╗ń╗ōÕēŹķØóµłæõ╗¼õĖŠńÜäõŠŗÕŁÉ
┬Ā
2.Õ£©õ┐«µö╣ÕÉÄńÜäĶ┐ÉĶĪīµ¼ĪµĢ░ÕćĮµĢ░õĖŁ’╝īÕŬõ┐ØńĢÖµ£Ćķ½śķśČķĪ╣ŃĆé
3.Õ”éµ×£µ£Ćķ½śķśČķĪ╣ÕŁśÕ£©õĖöõĖŹµś»1’╝īÕłÖÕÄ╗ķÖżõĖÄĶ┐ÖõĖ¬ķĪ╣ńøĖõ╣śńÜäÕĖĖµĢ░ŃĆé
ÕŠŚÕł░ńÜäń╗ōµ×£Õ░▒µś»Õż¦OķśČŃĆé
┬Ā
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā Õōł’╝īõ╗┐õĮøµś»ÕŠŚÕł░õ║åµĖĖµłÅµö╗ńĢźõĖƵĀĘ’╝īµłæõ╗¼ÕźĮÕāÅÕĘ▓ń╗ÅÕŠŚÕł░õ║åõĖĆõĖ¬µÄ©Õ»╝ń«Śµ│ĢµŚČķŚ┤ÕżŹµØéÕ║”ńÜäõĖćĶāĮÕģ¼Õ╝ÅŃĆéÕÅ»õ║ŗÕ«×õĖŖ’╝īÕłåµ×ÉõĖĆõĖ¬ń«Śµ│ĢńÜ䵌ČķŚ┤ÕżŹµØéÕ║”’╝īµ▓Īµ£ēĶ┐Öõ╣łń«ĆÕŹĢ’╝īµłæõ╗¼Ķ┐śķ£ĆĶ”üÕżÜń£ŗÕćĀõĖ¬õŠŗÕŁÉŃĆé
┬Ā
2.9.3┬ĀÕĖĖµĢ░ķśČ
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā ķ”¢ÕģłķĪ║Õ║Åń╗ōµ×äńÜ䵌ČķŚ┤ÕżŹµØéÕ║”ŃĆéõĖŗķØóĶ┐ÖõĖ¬ń«Śµ│Ģ’╝īõ╣¤Õ░▒µś»ÕłÜµēŹńÜäń¼¼õ║īń¦Źń«Śµ│Ģ’╝īõĖ║õ╗Ćõ╣łµŚČķŚ┤ÕżŹµØéÕ║”õĖŹµś»O(3)’╝īĶĆīµś»O(1)ŃĆé
┬Ā
┬Ā
┬Ā
- int┬Āsum┬Ā=┬Ā0,n┬Ā=┬Ā100;┬Ā┬Ā/*µē¦ĶĪīõĖƵ¼Ī*/┬Ā┬Ā
- sum┬Ā=┬Ā(1+n)*n/2;┬Ā┬Ā┬Ā/*µē¦ĶĪīõĖƵ¼Ī*/┬Ā┬Ā
- printf("%d",┬Āsum);┬Ā┬Ā/*µē¦ĶĪīõĖƵ¼Ī*/┬Ā┬Ā
┬Ā
┬Ā
┬Ā
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā ÕÅ”Õż¢’╝īµłæõ╗¼Ķ»Ģµā│õĖĆõĖŗ’╝īÕ”éµ×£Ķ┐ÖõĖ¬ń«Śµ│ĢÕĮōõĖŁńÜäĶ»ŁÕÅźsum=(1+n)*n/2µ£ē10ÕÅź’╝īÕŹ│’╝Ü
┬Ā
┬Ā
┬Ā
- int┬Āsum┬Ā=┬Ā0,┬Ān┬Ā=┬Ā100;┬Ā/*µē¦ĶĪīõĖƵ¼Ī*/┬Ā┬Ā
- sum┬Ā=┬Ā(1+n)*n/2;┬Ā┬Ā┬Ā/*µē¦ĶĪīń¼¼1µ¼Ī*/┬Ā┬Ā
- sum┬Ā=┬Ā(1+n)*n/2;┬Ā┬Ā┬Ā/*µē¦ĶĪīń¼¼2µ¼Ī*/┬Ā┬Ā
- sum┬Ā=┬Ā(1+n)*n/2;┬Ā┬Ā┬Ā/*µē¦ĶĪīń¼¼3µ¼Ī*/┬Ā┬Ā
- sum┬Ā=┬Ā(1+n)*n/2;┬Ā┬Ā┬Ā/*µē¦ĶĪīń¼¼4µ¼Ī*/┬Ā┬Ā
- sum┬Ā=┬Ā(1+n)*n/2;┬Ā┬Ā┬Ā/*µē¦ĶĪīń¼¼5µ¼Ī*/┬Ā┬Ā
- sum┬Ā=┬Ā(1+n)*n/2;┬Ā┬Ā┬Ā/*µē¦ĶĪīń¼¼6µ¼Ī*/┬Ā┬Ā
- sum┬Ā=┬Ā(1+n)*n/2;┬Ā┬Ā┬Ā/*µē¦ĶĪīń¼¼7µ¼Ī*/┬Ā┬Ā
- sum┬Ā=┬Ā(1+n)*n/2;┬Ā┬Ā┬Ā/*µē¦ĶĪīń¼¼8µ¼Ī*/┬Ā┬Ā
- sum┬Ā=┬Ā(1+n)*n/2;┬Ā┬Ā┬Ā/*µē¦ĶĪīń¼¼9µ¼Ī*/┬Ā┬Ā
- sum┬Ā=┬Ā(1+n)*n/2;┬Ā┬Ā┬Ā/*µē¦ĶĪīń¼¼10µ¼Ī*/┬Ā┬Ā
- printf("%d",sum);┬Ā┬Ā/*µē¦ĶĪīõĖƵ¼Ī*/┬Ā┬Ā┬Ā
┬Ā
┬Ā
┬Ā
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā µ│©µäÅ’╝īõĖŹń«ĪĶ┐ÖõĖ¬ÕĖĖµĢ░µś»ÕżÜÕ░æ’╝īµłæõ╗¼ķāĮĶ«░õĮ£O(1)’╝īĶĆīõĖŹĶāĮµś»O(3)ŃĆüO(12)ńŁēÕģČõ╗¢õ╗╗õĮĢµĢ░ÕŁŚŃĆéĶ┐Öµś»ÕłØÕŁ”ĶĆģÕĖĖÕĖĖńŖ»ńÜäķöÖĶ»»ŃĆé
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā Õ»╣õ║ÄÕłåµö»ń╗ōµ×äĶĆīĶ©Ć’╝īµŚĀĶ«║µś»ń£¤’╝īĶ┐śµś»Õüć’╝īµē¦ĶĪīńÜäµ¼ĪµĢ░ķāĮµś»µüÆÕ«ÜńÜä’╝īõĖŹõ╝ÜķÜÅńØĆnńÜäÕÅśÕż¦ĶĆīÕÅæńö¤ÕÅśÕī¢’╝īµēĆõ╗źÕŹĢń║»ńÜäÕłåµö»ń╗ōµ×ä’╝łõĖŹÕīģÕɽգ©ÕŠ¬ńÄ»ń╗ōµ×äõĖŁ’╝ē’╝īÕģȵŚČķŚ┤ÕżŹµØéÕ║”õ╣¤µś»O(1)ŃĆé
┬Ā
2.9.4┬Āń║┐µĆ¦ķśČ
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā ÕŠ¬ńÄ»ń╗ōµ×äÕ░▒õ╝ÜÕżŹµØéÕŠłÕżÜŃĆéĶ”üńĪ«Õ«Üµ¤ÉõĖ¬ń«Śµ│ĢńÜäķśČµ¼Ī’╝īµłæõ╗¼ÕĖĖÕĖĖķ£ĆĶ”üńĪ«Õ«Üµ¤ÉõĖ¬ńē╣Õ«ÜĶ»ŁÕÅźµł¢µ¤ÉõĖ¬Ķ»ŁÕÅźķøåĶ┐ÉĶĪīńÜäµ¼ĪµĢ░ŃĆéÕøĀµŁż’╝īµłæõ╗¼Ķ”üÕłåµ×Éń«Śµ│ĢńÜäÕżŹµØéÕ║”’╝īÕģ│ķö«Õ░▒µś»Ķ”üÕłåµ×ÉÕŠ¬ńÄ»ń╗ōµ×äńÜäĶ┐ÉĶĪīµāģÕåĄŃĆé
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā õĖŗķØóĶ┐Öµ«Ąõ╗ŻńĀü’╝īÕ«āńÜäÕŠ¬ńÄ»ńÜ䵌ČķŚ┤ÕżŹµØéÕ║”õĖ║O(n)ŃĆéÕøĀõĖ║ÕŠ¬ńÄ»õĮōõĖŁńÜäõ╗ŻńĀüķĪ╗Ķ”üµē¦ĶĪīnµ¼ĪŃĆé
┬Ā
┬Ā
┬Ā
- int┬Āi;┬Ā┬Ā
- for(i┬Ā=┬Ā0;┬Āi┬Ā<┬Ān;┬Āi++)┬Ā┬Ā
- {┬Ā┬Ā
- ┬Ā┬Ā┬Ā/*µŚČķŚ┤ÕżŹµØéÕ║”õĖ║O(1)ńÜäń©ŗÕ║ŵŁźķ¬żÕ║ÅÕłŚ*/┬Ā┬Ā
- }┬Ā┬Ā
┬Ā
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā ķéŻõ╣łõĖŗķØóńÜäĶ┐Öµ«Ąõ╗ŻńĀü’╝īµŚČķŚ┤ÕżŹµØéÕ║”ÕÅłµś»ÕżÜÕ░æÕæó’╝¤
┬Ā
┬Ā
┬Ā
- int┬Ācount┬Ā=┬Ā1;┬Ā┬Ā
- while┬Ā(count┬Ā<┬Ān)┬Ā┬Ā
- {┬Ā┬Ā
- ┬Ā┬Ā┬Ācount┬Ā=┬Ācount┬Ā*┬Ā2;┬Ā┬Ā
- ┬Ā┬Ā┬Ā/*µŚČķŚ┤ÕżŹµØéÕ║”õĖ║O(1)ńÜäń©ŗÕ║ŵŁźķ¬żÕ║ÅÕłŚ*/┬Ā┬Ā
- }┬Ā┬Ā
┬Ā
┬Ā
2.9.6┬ĀÕ╣│µ¢╣ķśČ
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā õĖŗķØóńÜäõŠŗÕŁÉµś»õĖĆõĖ¬ÕŠ¬ńÄ»ÕĄīÕźŚ’╝īÕ«āńÜäÕåģÕŠ¬ńÄ»ÕłÜµēŹµłæõ╗¼ÕĘ▓ń╗ÅÕłåµ×ÉĶ┐ć’╝īµŚČķŚ┤ÕżŹµØéÕ║”õĖ║O(n)ŃĆé
┬Ā
┬Ā
┬Ā
- int┬Āi,j;┬Ā┬Ā
- for(i┬Ā=┬Ā0;┬Āi┬Ā<┬Ān;┬Āi++)┬Ā┬Ā
- {┬Ā┬Ā
- ┬Ā┬Ā┬Āfor┬Ā(j┬Ā=┬Ā0;┬Āj┬Ā<┬Ān;j++)┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā
- ┬Ā┬Ā┬Ā{┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā
- ┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā/*µŚČķŚ┤ÕżŹµØéÕ║”õĖ║O(1)ńÜäń©ŗÕ║ŵŁźķ¬żÕ║ÅÕłŚ*/┬Ā┬Ā
- ┬Ā┬Ā┬Ā}┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā
- }┬Ā┬Ā
┬Ā
┬Ā
┬Ā
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā Õ”éµ×£Õż¢ÕŠ¬ńÄ»ńÜäÕŠ¬ńÄ»µ¼ĪµĢ░µö╣õĖ║õ║åm’╝īµŚČķŚ┤ÕżŹµØéÕ║”Õ░▒ÕÅśõĖ║O(m├Śn)ŃĆé
┬Ā
┬Ā
┬Ā
- int┬Āi,j;┬Ā┬Ā
- for(i┬Ā=┬Ā0;┬Āi┬Ā<┬Ām;┬Āi++)┬Ā┬Ā
- {┬Ā┬Ā
- ┬Ā┬Ā┬Āfor┬Ā(j┬Ā=┬Ā0;┬Āj┬Ā<┬Ān;┬Āj++)┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā
- ┬Ā┬Ā┬Ā{┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā
- ┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā/*µŚČķŚ┤ÕżŹµØéÕ║”õĖ║O(1)ńÜäń©ŗÕ║ŵŁźķ¬żÕ║ÅÕłŚ*/┬Ā┬Ā
- ┬Ā┬Ā┬Ā}┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā
- }┬Ā┬Ā
┬Ā
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā ķéŻõ╣łõĖŗķØóĶ┐ÖõĖ¬ÕŠ¬ńÄ»ÕĄīÕźŚ’╝īÕ«āńÜ䵌ČķŚ┤ÕżŹµØéÕ║”µś»ÕżÜÕ░æÕæó’╝¤
┬Ā
┬Ā
┬Ā
- int┬Āi,j;┬Ā┬Ā
- for(i┬Ā=┬Ā0;┬Āi┬Ā<┬Ān;┬Āi++)┬Ā┬Ā
- {┬Ā┬Ā
- ┬Ā┬Ā┬Ā┬Āfor┬Ā(j┬Ā=┬Āi;┬Āj┬Ā<┬Ān;┬Āj++)┬Ā┬Ā/*µ│©µäÅint┬Āj┬Ā=┬ĀiĶĆīõĖŹµś»0*/┬Ā┬Ā
- ┬Ā┬Ā┬Ā┬Ā{┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā
- ┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā/*µŚČķŚ┤ÕżŹµØéÕ║”õĖ║O(1)ńÜäń©ŗÕ║ŵŁźķ¬żÕ║ÅÕłŚ*/┬Ā┬Ā
- ┬Ā┬Ā┬Ā┬Ā}┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā
- }┬Ā┬Ā
┬Ā
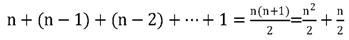
┬Ā
┬Ā
┬Ā
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā
┬Ā
┬Ā
┬Ā
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā ńö©µłæõ╗¼µÄ©Õ»╝Õż¦OķśČńÜäµ¢╣µ│Ģ’╝īń¼¼õĖƵØĪ’╝īµ▓Īµ£ēÕŖĀµ│ĢÕĖĖµĢ░õĖŹõ║łĶĆāĶÖæ’╝øń¼¼õ║īµØĪ’╝īÕŬõ┐ØńĢÖµ£Ćķ½śķśČķĪ╣’╝īÕøĀµŁżõ┐ØńĢÖn2/2’╝øń¼¼õĖēµØĪ’╝īÕÄ╗ķÖżĶ┐ÖõĖ¬ķĪ╣ńøĖõ╣śńÜäÕĖĖµĢ░’╝īõ╣¤Õ░▒µś»ÕÄ╗ķÖż1/2’╝īµ£Ćń╗łĶ┐Öµ«Ąõ╗ŻńĀüńÜ䵌ČķŚ┤ÕżŹµØéÕ║”õĖ║O(n2)ŃĆé
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā õ╗ÄĶ┐ÖõĖ¬õŠŗÕŁÉ’╝īµłæõ╗¼õ╣¤ÕÅ»õ╗źÕŠŚÕł░õĖĆõĖ¬ń╗Åķ¬ī’╝īÕģČÕ«×ńÉåĶ¦ŻÕż¦OµÄ©Õ»╝õĖŹń«ŚķÜŠ’╝īķÜŠńÜ䵜»Õ»╣µĢ░ÕłŚńÜäõĖĆõ║øńøĖÕģ│Ķ┐Éń«Ś’╝īĶ┐Öµø┤ÕżÜńÜ䵜»ĶĆāÕ»¤õĮĀńÜäµĢ░ÕŁ”ń¤źĶ»åÕÆīĶāĮÕŖø’╝īµēĆõ╗źµā│ĶĆāńĀöńÜäµ£ŗÕÅŗ’╝īĶ”üµā│Õ£©µ▒éń«Śµ│ĢµŚČķŚ┤ÕżŹµØéÕ║”Ķ┐ÖķćīõĖŹÕż▒Õłå’╝īÕÅ»ĶāĮķ£ĆĶ”üÕ╝║Õī¢õĮĀńÜäµĢ░ÕŁ”’╝īńē╣Õł½µś»µĢ░ÕłŚµ¢╣ķØóńÜäń¤źĶ»åÕÆīĶ¦ŻķóśĶāĮÕŖøŃĆé
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā µłæõ╗¼ń╗¦ń╗Łń£ŗõŠŗÕŁÉ’╝īÕ»╣õ║ĵ¢╣µ│ĢĶ░āńö©ńÜ䵌ČķŚ┤ÕżŹµØéÕ║”ÕÅłÕ”éõĮĢÕłåµ×ÉŃĆé
┬Ā
┬Ā
┬Ā
- int┬Āi,j;┬Ā┬Ā
- for(i┬Ā=┬Ā0;┬Āi┬Ā<┬Ān;┬Āi++)┬Ā┬Ā
- {┬Ā┬Ā
- ┬Ā┬Ā┬Āfunction(i);┬Ā┬Ā
- }┬Ā┬Ā
┬Ā
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā õĖŖķØóĶ┐Öµ«Ąõ╗ŻńĀüĶ░āńö©õĖĆõĖ¬ÕćĮµĢ░functionŃĆé
┬Ā
- void┬Āfunction(int┬Ācount)┬Ā┬Ā
- {┬Ā┬Ā
- ┬Ā┬Ā┬Āprint(count);┬Ā┬Ā
- }┬Ā┬Ā
┬Ā
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā ÕüćÕ”éfunctionµś»õĖŗķØóĶ┐ÖµĀĘńÜä’╝Ü
┬Ā
┬Ā
┬Ā
- void┬Āfunction(int┬Ācount)┬Ā┬Ā
- {┬Ā┬Ā
- ┬Ā┬Ā┬Āint┬Āj;┬Ā┬Ā
- ┬Ā┬Ā┬Āfor┬Ā(j┬Ā=┬Ācount;┬Āj┬Ā<┬Ān;j++)┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā
- ┬Ā┬Ā┬Ā{┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā
- ┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā/*µŚČķŚ┤ÕżŹµØéÕ║”õĖ║O(1)ńÜäń©ŗÕ║ŵŁźķ¬żÕ║ÅÕłŚ*/┬Ā┬Ā
- ┬Ā┬Ā┬Ā}┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā
- }┬Ā┬Ā┬Ā
┬Ā
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā õĖŗķØóĶ┐Öµ«ĄńøĖÕ»╣ÕżŹµØéńÜäĶ»ŁÕÅź’╝Ü
┬Ā
┬Ā
┬Ā
- n++;┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā/*µē¦ĶĪīµ¼ĪµĢ░õĖ║1*/┬Ā┬Ā
- function(n);┬Ā┬Ā┬Ā┬Ā┬Ā/*µē¦ĶĪīµ¼ĪµĢ░õĖ║n*/┬Ā┬Ā
- int┬Āi,j;┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā
- for(i┬Ā=┬Ā0;┬Āi┬Ā<┬Ān;┬Āi++)┬Ā┬Ā/*µē¦ĶĪīµ¼ĪµĢ░õĖ║n2*/┬Ā┬Ā
- {┬Ā┬Ā
- ┬Ā┬Ā┬Āfunction┬Ā(i);┬Ā┬Ā
- }┬Ā┬Ā
- for(i┬Ā=┬Ā0;┬Āi┬Ā<┬Ān;┬Āi++)┬Ā┬Ā/*µē¦ĶĪīµ¼ĪµĢ░õĖ║n(n┬Ā+┬Ā1)/2*/┬Ā┬Ā
- {┬Ā┬Ā
- ┬Ā┬Ā┬Āfor┬Ā(j┬Ā=┬Āi;j┬Ā<┬Ān;┬Āj++)┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā
- ┬Ā┬Ā┬Ā{┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā
- ┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā/*µŚČķŚ┤ÕżŹµØéÕ║”õĖ║O(1)ńÜäń©ŗÕ║ŵŁźķ¬żÕ║ÅÕłŚ*/┬Ā┬Ā
- ┬Ā┬Ā┬Ā}┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā
- }┬Ā┬Ā
┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā┬Ā Õ«āńÜäµē¦ĶĪīµ¼ĪµĢ░![]() ’╝īµĀ╣µŹ«µÄ©Õ»╝Õż¦OķśČńÜäµ¢╣µ│Ģ’╝īµ£Ćń╗łĶ┐Öµ«Ąõ╗ŻńĀüńÜ䵌ČķŚ┤ÕżŹµØéÕ║”õ╣¤µś»O(n2)ŃĆé
’╝īµĀ╣µŹ«µÄ©Õ»╝Õż¦OķśČńÜäµ¢╣µ│Ģ’╝īµ£Ćń╗łĶ┐Öµ«Ąõ╗ŻńĀüńÜ䵌ČķŚ┤ÕżŹµØéÕ║”õ╣¤µś»O(n2)ŃĆé
┬Ā
µ£¼µ¢ćĶĮ¼Ķ欒╝Ühttp://dsr-22.iteye.com/blog/1139218








ńøĖÕģ│µÄ©ĶŹÉ
Õģ│õ║ÄķĆÆÕĮÆń«Śµ│ĢµŚČķŚ┤ÕżŹµØéÕ║”Õłåµ×ÉńÜäµÄóĶ«©’╝īµś»õĖĆõĖ¬µĘ▒ÕģźńÉåĶ¦Żń«Śµ│ĢµĢłńÄćÕÆīõ╝śÕī¢ńÜäÕģ│ķö«Ķ««ķóśŃĆéķĆÆÕĮÆ’╝īõĮ£õĖ║Ķ¦ŻÕå│ķŚ«ķóśńÜäõĖĆń¦ŹÕ╝║Õż¦ÕĘźÕģĘ’╝īÕģȵ£¼Ķ┤©µś»Õ░åÕżŹµØéķŚ«ķóśÕłåĶ¦ŻõĖ║µø┤ń«ĆÕŹĢńÜäÕŁÉķŚ«ķóś’╝īķĆÜĶ┐ćµ▒éĶ¦ŻĶ┐Öõ║øÕŁÉķŚ«ķóśµØźĶŠŠÕł░µ£Ćń╗łĶ¦ŻÕå│µ¢╣µĪłńÜäńø«ńÜäŃĆéńäČĶĆī’╝ī...
µĀ╣µŹ«ń╗Öիܵ¢ćõ╗ČńÜäõ┐Īµü»’╝īµłæõ╗¼ÕÅ»õ╗źĶ»”ń╗åÕ£░µÄóĶ«©ŌĆ£ń«Śµ│ĢµŚČķŚ┤ÕżŹµØéÕ║”ŌĆØńÜäńøĖÕģ│ń¤źĶ»åńé╣ŃĆ鵌ČķŚ┤ÕżŹµØéÕ║”µś»ĶĪĪķćÅń«Śµ│ĢĶ┐ÉĶĪīµŚČķŚ┤ķÜÅĶŠōÕģźĶ¦äµ©ĪÕó×ķĢ┐ĶĆīÕÅśÕī¢ńÜäÕćĮµĢ░’╝īÕ«āÕ£©Ķ«Īń«Śµ£║ń¦æÕŁ”õĖÄń╝¢ń©ŗķóåÕ¤¤µē«µ╝öńØĆĶć│Õģ│ķćŹĶ”üńÜäĶ¦ÆĶē▓ŃĆéµÄźõĖŗµØź’╝īµłæõ╗¼Õ░åÕø┤ń╗Ģõ╗źõĖŗÕćĀõĖ¬...
Õ£©Ķ«Īń«Śµ£║ń¦æÕŁ”õĖŁ’╝īń«Śµ│ĢńÜä...µ£¼µ¢ćĶ»”ń╗åõ╗ŗń╗Źõ║åµŚČķŚ┤ÕżŹµØéÕ║”Õłåµ×ÉńÜäķćŹĶ”üµĆ¦ÕÆīµ¢╣µ│Ģ’╝īķĆÜĶ┐ćÕģĘõĮōńż║õŠŗÕ▒Ģńż║õ║åÕ”éõĮĢÕ»╣õĖŹÕÉīµĢ░µŹ«ń╗ōµ×äÕÆīń«Śµ│ĢĶ┐øĶĪīµŚČķŚ┤ÕżŹµØéÕ║”Õłåµ×ÉŃĆéÕĖīµ£øĶ┐ÖĶāĮÕĖ«ÕŖ®Ķ»╗ĶĆģµø┤ÕźĮÕ£░ńÉåĶ¦ŻµŚČķŚ┤ÕżŹµØéÕ║”ńÜäµ”éÕ┐Ą’╝īµÅÉķ½śń«Śµ│ĢÕłåµ×ÉÕÆīĶ«ŠĶ«ĪńÜäĶāĮÕŖøŃĆé
µĀ╣ÕÅĘnµ«ĄÕĮÆÕ╣ȵÄÆÕ║Åń«Śµ│Ģµś»õĖĆń¦Źõ╝śÕī¢Ķ┐ćńÜäÕĮÆÕ╣ȵÄÆÕ║ÅńŁ¢ńĢź’╝īÕ«āńÜäõĖ╗Ķ”üńø«µĀ浜»ÕćÅÕ░æµ»öĶŠāÕÆīõ║żµŹóµōŹõĮ£ńÜäµ¼ĪµĢ░’╝īõ╗ÄĶĆīÕ£©ÕżäńÉåÕż¦µĢ░µŹ«ķøåµŚČµÅÉķ½śµĢłńÄćŃĆé...ńÉåĶ¦ŻÕģČÕĘźõĮ£ÕĤńÉåÕÆīµŚČķŚ┤ÕżŹµØéÕ║”Õłåµ×ɵ£ēÕŖ®õ║ĵłæõ╗¼Õ£©Õ«×ķÖģÕ║öńö©õĖŁķĆēµŗ®ÕÉłķĆéńÜäµÄÆÕ║Åń«Śµ│ĢŃĆé
Õ║öńö©ķ®¼Õ░öń¦æÕż½ķōŠµ©ĪÕ×ŗĶ»üµśÄõ║åķüŚõ╝Āń”üÕ┐īµÉ£ń┤óń«Śµ│Ģµś»õ╗źµ”éńÄć1µöȵĢøÕł░Õģ©Õ▒Ƶ£Ćõ╝śĶ¦ŻńÜä,Õ╣ČÕ║öńö©µ▒éĶ¦ŻķÜŵ£║ń«Śµ│ĢµŚČķŚ┤ÕżŹµØéÕ║”ńÜäµ¢╣µ│Ģ,ÕŹ│µ▒éĶ¦Żń«Śµ│ĢńÜäµ£¤µ£øµöȵĢøµŚČķŚ┤,õ╝░ń«Śõ║åĶ»źń«Śµ│ĢńÜ䵌ČķŚ┤ÕżŹµØéÕ║”,ń╗ōµ×£Ķ»üµśÄĶ»źń«Śµ│ĢńÜ䵌ČķŚ┤ÕżŹµØéÕ║”õĖĵēĆÕŠŚĶ¦ŻńÜäÕżÜµĀʵƦŃĆü...
Õ£©Ķ«Īń«Śµ£║ń¦æÕŁ”õĖŁ’╝īµÄÆÕ║Åń«Śµ│Ģµś»µĢ░µŹ«ÕżäńÉåńÜäķćŹĶ”üń╗䵳Éķā©Õłå’╝īÕ«āõ╗¼ńö©õ║ÄÕ░åõĖĆń╗䵌ĀÕ║ÅńÜäµĢ░µŹ«µīēńģ¦ńē╣Õ«ÜńÜäķĪ║Õ║ŵÄÆÕłŚŃĆéÕ£©Javań╝¢ń©ŗĶ»ŁĶ©ĆõĖŁ’╝īÕ«×ńÄ░...ńäČĶĆī’╝īõ║åĶ¦ŻÕ¤║µ£¼µÄÆÕ║Åń«Śµ│ĢńÜäÕĤńÉåÕÆīµŚČķŚ┤ÕżŹµØéÕ║”Õłåµ×ÉÕ»╣õ║Äõ╝śÕī¢õ╗ŻńĀüÕÆīĶ¦ŻÕå│ńē╣Õ«ÜķŚ«ķóśõ╗ŹńäČĶć│Õģ│ķćŹĶ”üŃĆé
ńÉåĶ¦ŻÕ╣ČÕłåµ×Éń«Śµ│ĢńÜ䵌ČķŚ┤ÕżŹµØéÕ║”µ£ēÕŖ®õ║Äõ╝śÕī¢ń©ŗÕ║ÅµĆ¦ĶāĮŃĆé µÄźńØƵś»**0-1ĶāīÕīģķŚ«ķóś**’╝īĶ┐Öµś»õĖĆõĖ¬ń╗ÅÕģĖńÜäń╗äÕÉłõ╝śÕī¢ķŚ«ķóśŃĆéÕ£©0-1ĶāīÕīģķŚ«ķóśõĖŁ’╝īµłæõ╗¼µ£ēõĖĆõĖ¬Õ«╣ķćŵ£ēķÖÉńÜäĶāīÕīģ’╝īķćīķØóĶŻģµ£ēõĖŹÕÉīķćŹķćÅÕÆīõ╗ĘÕĆ╝ńÜäńē®Õōü’╝īńø«µĀ浜»Õ£©õĖŹĶČģĶ┐ćĶāīÕīģµĆ╗Õ«╣ķćÅńÜä...
Õ£©ń«Śµ│ĢµŚČķŚ┤ÕżŹµØéÕ║”ńÜäĶ«Īń«ŚõĖŁ’╝īµłæõ╗¼ķ£ĆĶ”üÕłåµ×Éń«Śµ│ĢńÜäķóæÕ║”’╝īÕŹ│µ»ÅõĖ¬Ķ»ŁÕÅźńÜäµē¦ĶĪīµ¼ĪµĢ░ŃĆéķĆÜÕĖĖµāģÕåĄõĖŗ’╝īµłæõ╗¼ÕÅ»õ╗źõĮ┐ńö©ÕŠ¬ńÄ»õĖŹÕÅśķćÅńÜäµ¢╣µ│ĢµØźĶ«Īń«ŚķóæÕ║”’╝īńäČÕÉĵĀ╣µŹ«ķóæÕ║”Ķ«Īń«Śń«Śµ│ĢńÜ䵌ČķŚ┤ÕżŹµØéÕ║”ŃĆé õŠŗÕ”é’╝īÕ£©õŠŗ 2.1 õĖŁ’╝īµłæõ╗¼ÕÅ»õ╗źń£ŗÕł░’╝īĶ»ŁÕÅź 1 ...
ÕÉäń¦ŹÕåģķā©µÄÆÕ║Åń«Śµ│ĢńÜ䵌ČķŚ┤ÕżŹµØéÕ║”Õłåµ×Éń╗ōµ×£ÕŬń╗ÖÕć║õ║åń«Śµ│Ģµē¦ĶĪīµŚČķŚ┤ńÜäķśČ’╝īµł¢Õż¦µ”éµē¦ĶĪīµŚČķŚ┤ŃĆéĶ»ĢķĆÜĶ┐ćķÜŵ£║ńÜäµĢ░µŹ«µ»öĶŠāÕÉäń«Śµ│ĢńÜäÕģ│ķö«ÕŁŚµ»öĶŠāµ¼ĪµĢ░ÕÆīÕģ│ķö«ÕŁŚń¦╗ÕŖ©µ¼ĪµĢ░’╝īõ╗źÕÅ¢ÕŠŚńø┤Ķ¦éµä¤ÕÅŚŃĆé
### ń«Śµ│ĢńÜ䵌ČķŚ┤ÕżŹµØéÕ║”õĖÄń®║ķŚ┤ÕżŹµØéÕ║”Ķ»”Ķ¦Ż #### õĖĆŃĆüń«Śµ│ĢÕżŹµØéÕ║”µ”éĶ┐░ Õ£©Ķ«Īń«Śµ£║ń¦æÕŁ”ķóåÕ¤¤’╝īń«Śµ│ĢńÜ䵌ČķŚ┤ÕżŹµØéÕ║”õĖÄń®║ķŚ┤ÕżŹµØéÕ║”µś»ĶĪĪķćÅõĖĆõĖ¬ń«Śµ│ĢµĢłńÄćńÜäķćŹĶ”üµīćµĀćŃĆ鵌ČķŚ┤ÕżŹµØéÕ║”Õģ│µ│©ńÜ䵜»ń«Śµ│Ģµē¦ĶĪīµŚČķŚ┤ńÜäÕó×ķĢ┐ķƤńÄć’╝īĶĆīń®║ķŚ┤ÕżŹµØéÕ║”ÕłÖõŠ¦ķćŹ...
1. ķ”¢Õģłõ║¦ńö¤Ķ”üĶ┐øĶĪīµÄÆÕ║ÅńÜäµĢ┤ÕĮóµĢ░ń╗ä’╝łÕÅ»õ╗źõ┐ØÕŁśÕ£©µ¢ćõ╗ČõĖŁ...2. Ķ░āńö©ÕÉäń¦ŹµÄÆÕ║ŵ¢╣µ│ĢÕ»╣µĢ░ń╗äµÄÆÕ║Å’╝īÕ╣ČĶ«░ÕĮĢĶŖ▒Ķ┤╣µŚČķŚ┤ Õ»╣õ║ĵø┤ÕżÜµø┤ķ½śń║¦ńÜäµÄÆÕ║Åń«Śµ│Ģ’╝īõ╗źÕÉÄõ╝ÜÕ«×ńÄ░’╝īÕÅ”Õż¢’╝īÕ»╣õ║ÄÕżŹµØéÕŁŚń¼”õĖ▓µÄÆÕ║Å’╝īĶ┐Öõ║øń«ĆÕŹĢµÄÆÕ║ÅÕ╣ČõĖŹķĆéÕÉł’╝īĶ»Ęķććńö©µø┤ķ½śµĢłńÜäµ¢╣µ│Ģ
µ¢ćń½ĀõĖŁńÜäõĖēõĖ¬µÄ©Ķ«║ÕÅ»ĶāĮµČēÕÅŖõ║åń▒╗õ╝╝õ║ÄõĖŖĶ┐░ńÜäµĢ░ÕŁ”µÄ©Õ»╝Ķ┐ćń©ŗ’╝īÕ▒Ģńż║õ║åµ»ŹÕćĮµĢ░ńÉåĶ«║Õ£©ķĆÆÕĮÆń«Śµ│ĢµŚČķŚ┤ÕżŹµØéÕ║”Õłåµ×ÉõĖŁńÜäÕ║öńö©ŃĆéĶ┐Öń¦ŹÕłåµ×ɵ¢╣µ│ĢõĖŹõ╗ģĶāĮń╗ÖÕć║µŚČķŚ┤ÕżŹµØéÕ║”ńÜäõĖŖńĢīµł¢õĖŗńĢī’╝īĶ┐śÕÅ»õ╗źÕ£©µ¤Éõ║øµāģÕåĄõĖŗµÅÉõŠøń▓ŠńĪ«ńÜ䵌ČķŚ┤ÕżŹµØéÕ║”ĶĪ©ĶŠŠÕ╝ÅŃĆéĶ┐Öõ║ø...
ń«Śµ│ĢÕżŹµØéÕ║”Õłåµ×ɵś»Ķ»äõ╝░ń«Śµ│ĢµĢłńÄćńÜäķćŹĶ”üÕĘźÕģĘ’╝īõĖ╗Ķ”üµČēÕÅŖµŚČķŚ┤ÕżŹµØéÕ║”ÕÆīń®║ķŚ┤ÕżŹµØéÕ║”õĖżõĖ¬µ¢╣ķØóŃĆéĶ┐ÖķŚ©Õ¤║ńĪĆĶ»Šń©ŗµŚ©Õ£©µĢÖµÄłÕ”éõĮĢÕłåµ×Éń«Śµ│ĢÕ£©ÕżäńÉåÕż¦Ķ¦äµ©ĪµĢ░µŹ«µŚČµēĆķ£ĆńÜäĶĄäµ║É’╝īÕĖ«ÕŖ®Õ╝ĆÕÅæĶĆģõ╝śÕī¢ń©ŗÕ║ÅµĆ¦ĶāĮŃĆé õĖĆŃĆüń«Śµ│ĢÕżŹµØéÕ║”ńÜäµ”éÕ┐Ą 1. µŚČķŚ┤...
Õ┐½ķƤµÄÆÕ║ÅńÜ䵌ČķŚ┤ÕżŹµØéÕ║”Õ£©µ£ĆÕźĮµāģÕåĄõĖŗõĖ║O(n log n)’╝īµ£ĆÕØŵāģÕåĄõĖŗõĖ║O(n^2)’╝īÕ╣│ÕØćµāģÕåĄõ╣¤µś»O(n log n)ŃĆéńö▒õ║ÄÕ£©µ»ÅõĖĆĶĮ«ÕłÆÕłåõĖŁ’╝īÕģāń┤ĀńÜäń¦╗ÕŖ©µ¼ĪµĢ░ÕÅ»ĶāĮÕ░Åõ║ĵ»öĶŠāµ¼ĪµĢ░’╝īµēĆõ╗źÕ┐½ķƤµÄÆÕ║ÅķĆÜÕĖĖĶó½Ķ«żõĖ║µś»Õ«×ķÖģÕ║öńö©õĖŁµĢłńÄćĶŠāķ½śńÜäµÄÆÕ║Åń«Śµ│ĢŃĆéõĮåÕģČ...
Õ£©Õłåµ×Éń«Śµ│ĢµŚČķŚ┤ÕżŹµØéÕ║”ńÜäõĖŖõĖŗµ¢ćõĖŁ’╝īĶ┐Öõ║øµ¢ćõ╗ČÕÅ»ĶāĮÕīģÕɽńż║õŠŗõ╗ŻńĀüµł¢µĄŗĶ»Ģńö©õŠŗ’╝īńö©µØźµ╝öńż║õĖŹÕÉīń«Śµ│ĢńÜ䵌ČķŚ┤ÕżŹµØéÕ║”Õłåµ×ÉŃĆé ".idea"ńø«ÕĮĢķĆÜÕĖĖÕŁśÕé©IntelliJ IDEAµł¢Android StudiońŁēIDEńÜäķĪ╣ńø«ķģŹńĮ«õ┐Īµü»’╝īĶ┐ÖÕÅ»ĶāĮµäÅÕæ│ńØĆĶ┐ÖõĖ¬ÕÄŗń╝®Õīģµś»...
µ£¼Õ«×ķ¬īµĄŗĶ»ĢńÜäõĖ╗ķóśĶüÜńä”õ║ÄÕĀåµÄÆÕ║Åń«Śµ│ĢńÜ䵌ČķŚ┤ÕżŹµØéÕ║”Õłåµ×É’╝īńö▒ĶāĪõ╣”µÖŚĶ┐øĶĪīńĀöń®ČŃĆéÕĀåµÄÆÕ║ŵś»õĖĆń¦ŹÕ¤║õ║ĵ»öĶŠāńÜäµÄÆÕ║Åń«Śµ│Ģ’╝īÕģČÕ¤║µ£¼µĆصā│µś»Õ░åÕŠģµÄÆÕ║ÅńÜäµĢ░µŹ«µ×äķĆĀµłÉõĖĆõĖ¬Õż¦ķĪČÕĀåµł¢Õ░ÅķĪČÕĀå’╝īńäČÕÉÄķĆÜĶ┐ćõ║żµŹóÕĀåķĪČÕģāń┤ĀõĖĵ£½Õ░ŠÕģāń┤Ā’╝īÕ░åµ£ĆÕż¦’╝łµł¢µ£ĆÕ░Å’╝ē...