二维码又称QR Code,QR全称Quick Response,是一个近几年来移动设备上超流行的一种编码方式,它比传统的Bar Code条形码能存更多的信息,也能表示更多的数据类型:比如:字符,数字,日文,中文等等。这两天学习了一下二维码图片生成的相关细节,觉得这个玩意就 是一个密码算法,在此写一这篇文章 ,揭露一下。供好学的人一同学习之。
关于QR Code Specification,可参看这个PDF:http://raidenii.net/files/datasheets/misc/qr_code.pdf
基础知识
首先,我们先说一下二维码一共有40个尺寸。官方叫版本Version。Version 1是21 x 21的矩阵,Version 2是 25 x 25的矩阵,Version 3是29的尺寸,每增加一个version,就会增加4的尺寸,公式是:(V-1)*4 + 21(V是版本号) 最高Version 40,(40-1)*4+21 = 177,所以最高是177 x 177 的正方形。
下面我们看看一个二维码的样例:
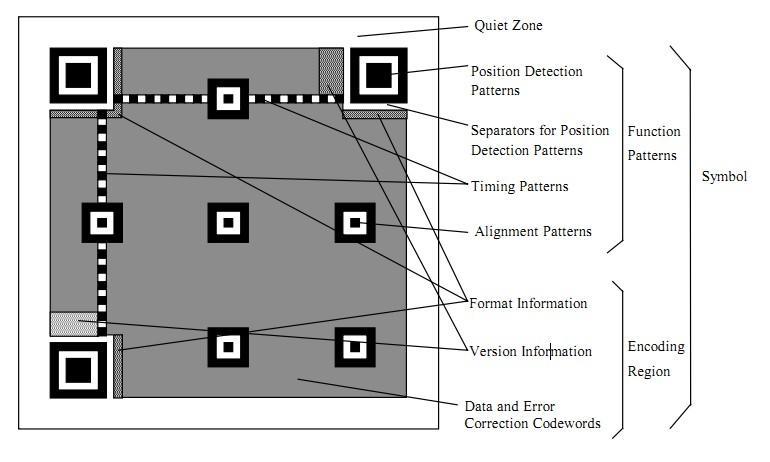
定位图案
- Position Detection Pattern是定位图案,用于标记二维码的矩形大小。这三个定位图案有白边叫Separators for Postion Detection Patterns。之所以三个而不是四个意思就是三个就可以标识一个矩形了。
- Timing Patterns也是用于定位的。原因是二维码有40种尺寸,尺寸过大了后需要有根标准线,不然扫描的时候可能会扫歪了。
- Alignment Patterns 只有Version 2以上(包括Version2)的二维码需要这个东东,同样是为了定位用的。
功能性数据
- Format Information 存在于所有的尺寸中,用于存放一些格式化数据的。
- Version Information 在 >= Version 7以上,需要预留两块3 x 6的区域存放一些版本信息。
数据码和纠错码
- 除了上述的那些地方,剩下的地方存放 Data Code 数据码 和 Error Correction Code 纠错码。
数据编码
我们先来说说数据编码。QR码支持如下的编码:
Numeric mode 数字编码,从0到9。如果需要编码的数字的个数不是3的倍数,那么,最后剩下的1或2位数会被转成4或7bits,则其它的每3位数字会被编成 10,12,14bits,编成多长还要看二维码的尺寸(下面有一个表Table 3说明了这点)
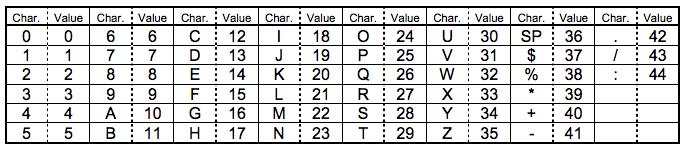
Alphanumeric mode 字符编码。包括 0-9,大写的A到Z(没有小写),以及符号$ % * + – . / : 包括空格。这些字符会映射成一个字符索引表。如下所示:(其中的SP是空格,Char是字符,Value是其索引值) 编码的过程是把字符两两分组,然后转成下表的45进制,然后转成11bits的二进制,如果最后有一个落单的,那就转成6bits的二进制。而编码模式和 字符的个数需要根据不同的Version尺寸编成9, 11或13个二进制(如下表中Table 3)
Byte mode, 字节编码,可以是0-255的ISO-8859-1字符。有些二维码的扫描器可以自动检测是否是UTF-8的编码。
Kanji mode 这是日文编码,也是双字节编码。同样,也可以用于中文编码。日文和汉字的编码会减去一个 值。如:在0X8140 to 0X9FFC中的字符会减去8140,在0XE040到0XEBBF中的字符要减去0XC140,然后把前两位拿出来乘以0XC0,然后再加上后两位,最 后转成13bit的编码。如下图示例:

Extended Channel Interpretation (ECI) mode 主要用于特殊的字符集。并不是所有的扫描器都支持这种编码。
Structured Append mode 用于混合编码,也就是说,这个二维码中包含了多种编码格式。
FNC1 mode 这种编码方式主要是给一些特殊的工业或行业用的。比如GS1条形码之类的。
简单起见,后面三种不会在本文 中讨论。
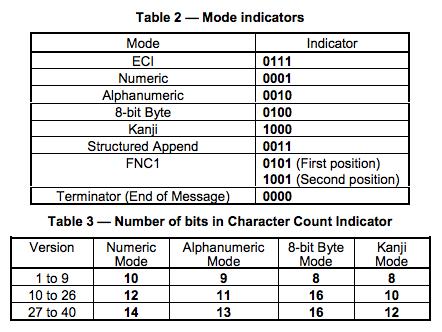
下面两张表中,
- Table 2 是各个编码格式的“编号”,这个东西要写在Format Information中。注:中文是1101
- Table 3 表示了,不同版本(尺寸)的二维码,对于,数字,字符,字节和Kanji模式下,对于单个编码的2进制的位数。(在二维码的规格说明书中,有各种各样的编码规范表,后面还会提到)
下面我们看几个示例,
示例一:数字编码
在Version 1的尺寸下,纠错级别为H的情况下,编码: 01234567
- 把上述数字分成三组: 012 345 67
- 把他们转成二进制: 012 转成 0000001100; 345 转成 0101011001; 67 转成 1000011。
- 把这三个二进制串起来: 0000001100 0101011001 1000011
- 把数字的个数转成二进制 (version 1-H是10 bits ): 8个数字的二进制是 0000001000
- 把数字编码的标志0001和第4步的编码加到前面: 0001 0000001000 0000001100 0101011001 1000011
示例二:字符编码
在Version 1的尺寸下,纠错级别为H的情况下,编码: AC-42
1. 从字符索引表中找到 AC-42 这五个字条的索引 (10,12,41,4,2)
2. 两两分组: (10,12) (41,4) (2)
3.把每一组转成11bits的二进制:
(10,12) 10*45+12 等于 462 转成 00111001110
(41,4) 41*45+4 等于 1849 转成 11100111001
(2) 等于 2 转成 000010
4. 把这些二进制连接起来:00111001110 11100111001 000010
5. 把字符的个数转成二进制 (Version 1-H为9 bits ): 5个字符,5转成 000000101
6. 在头上加上编码标识 0010 和第5步的个数编码: 0010 000000101 00111001110 11100111001 000010
结束符和补齐符
假如我们有个HELLO WORLD的字符串要编码,根据上面的示例二,我们可以得到下面的编码,
| 0010 | 000001011 | 01100001011 01111000110 10001011100 10110111000 10011010100 001101 |
我们还要加上结束符:
| 0010 | 000001011 | 01100001011 01111000110 10001011100 10110111000 10011010100 001101 | 0000 |
按8bits重排
如果所有的编码加起来不是8个倍数我们还要在后面加上足够的0,比如上面一共有78个bits,所以,我们还要加上2个0,然后按8个bits分好组:
00100000 01011011 00001011 01111000 11010001 01110010 11011100 01001101 01000011 01000000
补齐码(Padding Bytes)
最后,如果如果还没有达到我们最大的bits数的限制,我们还要加一些补齐码(Padding Bytes),Padding Bytes就是重复下面的两个bytes:11101100 00010001 (这两个二进制转成十进制是236和17,我也不知道为什么,只知道Spec上是这么写的)关于每一个Version的每一种纠错级别的最大Bits限 制,可以参看QR Code Spec的第28页到32页的Table-7一表。
假设我们需要编码的是Version 1的Q纠错级,那么,其最大需要104个bits,而我们上面只有80个bits,所以,还需要24个bits,也就是需要3个Padding Bytes,我们就添加三个,于是得到下面的编码:
00100000 01011011 00001011 01111000 11010001 01110010 11011100 01001101 01000011 01000000 11101100 00010001 11101100
纠错码
上面我们说到了一些纠错级别,Error Correction Code Level,二维码中有四种级别的纠错,这就是为什么二维码有残缺还能扫出来,也就是为什么有人在二维码的中心位置加入图标。
| L水平 | 7%的字码可被修正 |
| M水平 | 15%的字码可被修正 |
| Q水平 | 25%的字码可被修正 |
| H水平 | 30%的字码可被修正 |
那么,QR是怎么对数据码加上纠错码的?首先,我们需要对数据码进行分组,也就是分成不同的Block,然后对各个Block进行纠错编码,对于如何分组,我们可以查看QR Code Spec的第33页到44页的Table-13到Table-22的定义表。注意最后两列:
- Number of Error Code Correction Blocks :需要分多少个块。
- Error Correction Code Per Blocks:每一个块中的code个数,所谓的code的个数,也就是有多少个8bits的字节。
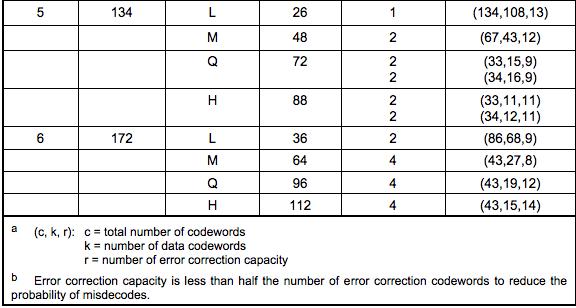
举个例子:上述的Version 5 + Q纠错级:需要4个Blocks(2个Blocks为一组,共两组),头一组的两个Blocks中各15个bits数据 + 各 9个bits的纠错码(注:表中的codewords就是一个8bits的byte)(再注:最后一例中的(c, k, r )的公式为:c = k + 2 * r,因为后脚注解释了:纠错码的容量小于纠错码的一半)
下图给一个5-Q的示例(因为二进制写起来会让表格太大,所以,我都用了十进制)
| 1 | 1 | 67 85 70 134 87 38 85 194 119 50 6 18 6 103 38 | 213 199 11 45 115 247 241 223 229 248 154 117 154 111 86 161 111 39 |
| 2 | 246 246 66 7 118 134 242 7 38 86 22 198 199 146 6 | 87 204 96 60 202 182 124 157 200 134 27 129 209 17 163 163 120 133 | |
| 2 | 1 | 182 230 247 119 50 7 118 134 87 38 82 6 134 151 50 7 | 148 116 177 212 76 133 75 242 238 76 195 230 189 10 108 240 192 141 |
| 2 | 70 247 118 86 194 6 151 50 16 236 17 236 17 236 17 236 | 235 159 5 173 24 147 59 33 106 40 255 172 82 2 131 32 178 236 |
注:二维码的纠错码主要是通过Reed-Solomon error correction(里 德-所罗门纠错算法)来实现的。对于这个算法,对于我来说是相当的复杂,里面有很多的数学计算,比如:多项式除法,把1-255的数映射成2的n次方 (0<=n<=255)的伽罗瓦域Galois Field之类的神一样的东西,以及基于这些基础的纠错数学公式,因为我的数据基础差,对于我来说太过复杂,所以我一时半会儿还有点没搞明白,还在学习 中,所以,我在这里就不展开说这些东西了。还请大家见谅了。(当然,如果有朋友很明白,也繁请教教我)
最终编码
穿插放置
如果你以为我们可以开始画图,你就错了。二维码的混乱技术还没有玩完,它还要把数据码和纠错码的各个codewords交替放在一起。如何交替呢,规则如下:
对于数据码:把每个块的第一个codewords先拿出来按顺度排列好,然后再取第一块的第二个,如此类推。如:上述示例中的Data Codewords如下:
| 块 1 | 67 | 85 | 70 | 134 | 87 | 38 | 85 | 194 | 119 | 50 | 6 | 18 | 6 | 103 | 38 | |
| 块 2 | 246 | 246 | 66 | 7 | 118 | 134 | 242 | 7 | 38 | 86 | 22 | 198 | 199 | 146 | 6 | |
| 块 3 | 182 | 230 | 247 | 119 | 50 | 7 | 118 | 134 | 87 | 38 | 82 | 6 | 134 | 151 | 50 | 7 |
| 块 4 | 70 | 247 | 118 | 86 | 194 | 6 | 151 | 50 | 16 | 236 | 17 | 236 | 17 | 236 | 17 | 236 |
我们先取第一列的:67, 246, 182, 70
然后再取第二列的:67, 246, 182, 70, 85,246,230 ,247
如此类推:67, 246, 182, 70, 85,246,230 ,247 ……… ……… ,38,6,50,17,7,236
对于纠错码,也是一样:
| 块 1 | 213 | 199 | 11 | 45 | 115 | 247 | 241 | 223 | 229 | 248 | 154 | 117 | 154 | 111 | 86 | 161 | 111 | 39 |
| 块 2 | 87 | 204 | 96 | 60 | 202 | 182 | 124 | 157 | 200 | 134 | 27 | 129 | 209 | 17 | 163 | 163 | 120 | 133 |
| 块 3 | 148 | 116 | 177 | 212 | 76 | 133 | 75 | 242 | 238 | 76 | 195 | 230 | 189 | 10 | 108 | 240 | 192 | 141 |
| 块 4 | 235 | 159 | 5 | 173 | 24 | 147 | 59 | 33 | 106 | 40 | 255 | 172 | 82 | 2 | 131 | 32 | 178 | 236 |
和数据码取的一样,得到:213,87,148,235,199,204,116,159,…… …… 39,133,141,236
然后,再把这两组放在一起(纠错码放在数据码之后)得到:
67, 246, 182, 70, 85, 246, 230, 247, 70, 66, 247, 118, 134, 7, 119, 86, 87, 118, 50, 194, 38, 134, 7, 6, 85, 242, 118, 151, 194, 7, 134, 50, 119, 38, 87, 16, 50, 86, 38, 236, 6, 22, 82, 17, 18, 198, 6, 236, 6, 199, 134, 17, 103, 146, 151, 236, 38, 6, 50, 17, 7, 236, 213, 87, 148, 235, 199, 204, 116, 159, 11, 96, 177, 5, 45, 60, 212, 173, 115, 202, 76, 24, 247, 182, 133, 147, 241, 124, 75, 59, 223, 157, 242, 33, 229, 200, 238, 106, 248, 134, 76, 40, 154, 27, 195, 255, 117, 129, 230, 172, 154, 209, 189, 82, 111, 17, 10, 2, 86, 163, 108, 131, 161, 163, 240, 32, 111, 120, 192, 178, 39, 133, 141, 236
Remainder Bits
最后再加上Reminder Bits,对于某些Version的QR,上面的还不够长度,还要加上Remainder Bits,比如:上述的5Q版的二维码,还要加上7个bits,Remainder Bits加零就好了。关于哪些Version需要多少个Remainder bit,可以参看QR Code Spec的第15页的Table-1的定义表。
画二维码图
Position Detection Pattern
首先,先把Position Detection图案画在三个角上。
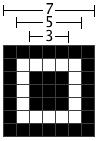
Alignment Pattern
然后,再把Alignment图案画上
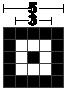
关于Alignment的位置,可以查看QR Code Spec的第81页的Table-E.1的定义表(下表是不完全表格)
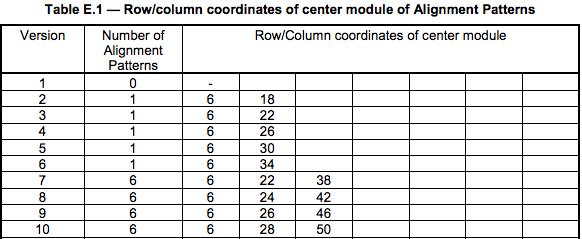
下图是根据上述表格中的Version8的一个例子(6,24,42)
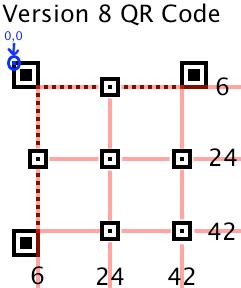
Timing Pattern
接下来是Timing Pattern的线(这个不用多说了)
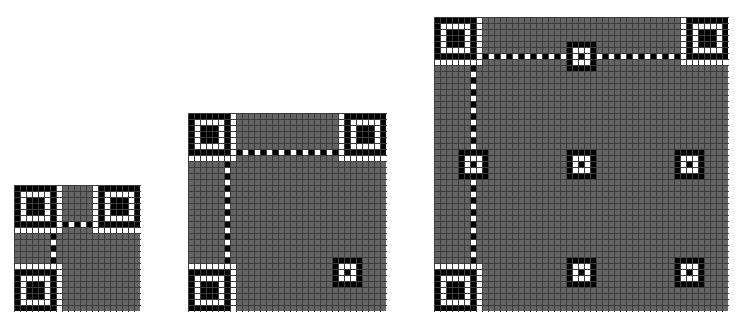
Format Information
再接下来是Formation Information,下图中的蓝色部分。
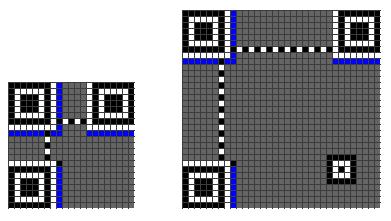
Format Information是一个15个bits的信息,每一个bit的位置如下图所示:(注意图中的Dark Module,那是永远出现的)
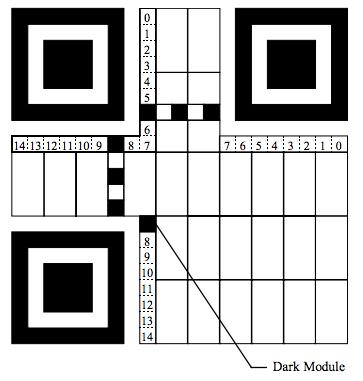
这15个bits中包括:
- 5个数据bits:其中,2个bits用于表示使用什么样的Error Correction Level, 3个bits表示使用什么样的Mask
- 10个纠错bits。主要通过BCH Code来计算
然后15个bits还要与101010000010010做XOR操作。这样就保证不会因为我们选用了00的纠错级别,以及000的Mask,从重造成全部为白色,这会增加我们的扫描器的图像识别的困难。
下面是一个示例:

关于Error Correction Level如下表所示:
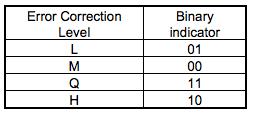
关于Mask图案如后面的Table 23所示。
Version Information
再接下来是Version Information(版本7以后需要这个编码),下图中的蓝色部分。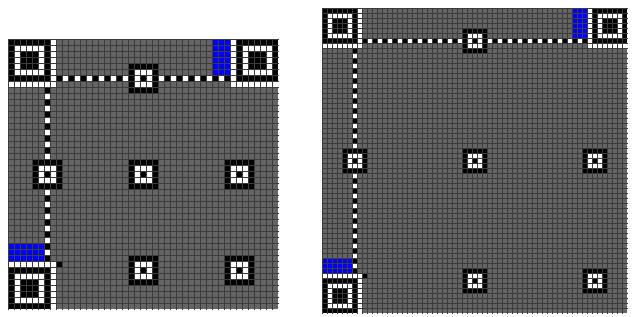
Version Information一共是18个bits,其中包括6个bits的版本号以及12个bits的纠错码,下面是一个示例:

而其填充位置如下:
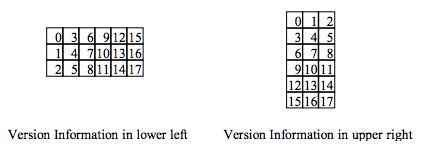
数据和数据纠错码
然后是填接我们的最终编码,最终编码的填充方式如下:从左下角开始沿着红线填我们的各个bits,1是黑色,0是白色。如果遇到了上面的非数据区,则绕开或跳过。

掩码图案
这样下来,我们的图就填好了,但是,也许那些点并不均衡,所以,我们还要做Masking操作(靠,还嫌不复杂)QR的Spec中说了,QR有8个 Mask你可以使用,如下所示:其中,各个mask的公式在各个图下面。所谓mask,说白了,就是和上面生成的图做XOR操作。Mask只会和数据区进 行XOR,不会影响功能区。

其Mask的标识码如下所示:(其中的i,j分别对应于上图的x,y)
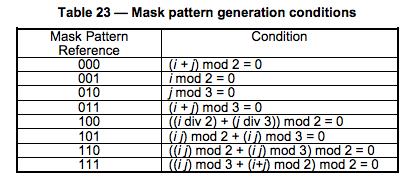
下面是Mask后的一些样子,我们可以看到被某些Mask XOR了的数据变得比较零散了。
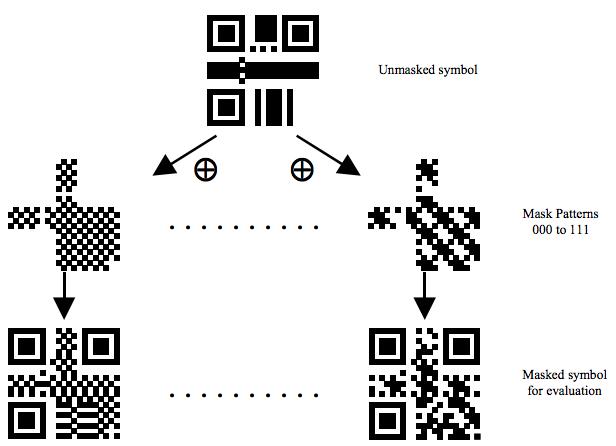
Mask过后的二维码就成最终的图了。









相关推荐
总的来说,Delphi二维码生成源码及程序的资源对于学习和开发具有二维码功能的Delphi应用非常有价值。通过研究和理解这些源码,开发者不仅可以掌握二维码的生成原理,还能学习到如何在Delphi环境中整合第三方库,提高...
【帝国CMS二维码生成插件】是一款专为帝国CMS系统设计的实用工具,旨在帮助网站管理员在不依赖外部API,如Google API的情况下,快速便捷地生成和集成二维码功能。这款插件简化了二维码生成的流程,使得在自己的网站...
理解这两个库的工作原理和API使用方法,对于开发C++二维码相关的应用至关重要。在实际开发过程中,你可能还需要关注性能优化、错误处理以及与其他系统组件(如图形界面或网络通信)的集成等问题。
通过解压并打开这个项目,你可以看到具体实现的细节,学习如何将二维码生成功能与Office应用无缝结合。 总之,"VSTO二维码生成源码(VB版)"涉及到的技术点包括VB.NET编程、ZXing.Net或其他二维码库的使用、VSTO...
对于开发者来说,通过阅读和分析源码,可以深入理解二维码生成的实现细节,提高编程技能,并在此基础上进行二次开发,例如添加更多高级功能,如自定义logo、二维码颜色等。 总之,"二维码生成器C#源码"是一个实用的...
Java QRCode二维码生成与识别是Java编程领域中的一个重要技术,主要应用于数据编码和快速信息交换。QRCode(Quick Response Code)是一种二维条码,能够存储大量的文本信息,包括字母、数字、汉字等,并且可以被各种...
二维码生成和加密程序是IT领域中一种常见的技术应用,它结合了编码与安全...理解其工作原理和编程实现,对于提升IT技能和解决实际问题具有重要意义。开发者可以通过掌握相关知识,创建更安全、高效的二维码解决方案。
如果它是源代码,我们可以预期看到相关的编程语言(如Java、Python或C#)、类库引用、函数调用等,这些都涉及到二维码生成和扫描的具体实现细节。如果是执行文件,它可能包含了编译后的程序,可以直接运行体验二维码...
通过对二维码生成与识别技术的研究,我们不仅深入了解了二维码的工作原理和技术细节,还实际实现了二维码的生成与识别功能。未来,随着技术的进步,二维码的应用将会更加广泛,对其研究也将不断深入。
总结来说,这个项目提供了一个基于VC6的二维码生成工具源码,利用了qrencode、libpng和zlib这三个开源库,实现了二维码的生成和相关数据处理功能。对于需要在Windows平台下开发二维码应用的开发者来说,这是一个很好...
【Delphi简易二维码生成器】是一款使用Delphi 7编程环境开发的应用程序,它具备生成二维码的功能,并且特别强调对中文字符的支持。在无需依赖任何第三方控件或动态链接库(DLL)的情况下,该生成器提供了简洁而实用...
【标题】:“vs2010二维码生成软件” 在信息技术领域,二维码(Quick Response Code...源代码的提供为学习和扩展这个功能提供了便利,使得开发者可以深入理解二维码生成的原理,并可能根据自己的需求进行定制化开发。
总的来说,这个压缩包提供的源码涵盖了二维码生成和解析的核心流程,对于理解二维码的工作原理和实现方式非常有帮助。开发者可以依据这些源码进行二次开发,定制自己的二维码工具,或者深入研究二维码的细节,如优化...
二维码在线生成网页源码是一种基于特定编码规则,能够将各种数据转化为可被手机扫描识别的图形化代码。这种源码通常包含HTML、...通过学习和理解这些源码,开发者可以自定义自己的二维码生成器,满足不同场景的需求。
在C语言中编写二维码生成器通常涉及到低级别的内存管理和数据结构操作,而MicroPython通过其简洁的语法和丰富的标准库,让这一过程变得更为直观。 描述中的“比之前的c的更容易用”暗示了这个项目可能提供了更友好...
二维码生成器是一款基于小程序开发的源码应用,它允许用户快速、...同时,也能掌握二维码生成的原理和实现方法,这在移动应用开发、营销推广等领域都大有裨益。对于想要提升技能的开发者而言,这是一个极好的实践案例。
.NET QRCode二维码生成小工具是基于C#编程语言和.NET框架开发的一款实用程序,它能够帮助用户快速便捷地创建和生成二维码。此工具的核心技术在于QRCode编码算法,这是一种广泛应用于移动设备和物联网中的二维条形码...