任务处理——最优化问题

问题描述：

Student A took 5 courses this semester. Below table lists due time to submit his homework from now on. It also lists the time to finish those works.

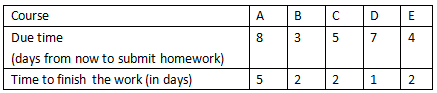
As the time is limited, some homework cannot be finished on time. What he can do is arranging his time in a smart way so that he can finish more homework on time. Please do bellowing work:

1) Write C program to get the right arrangement

2) Write makefile for this program

3) Write detail description of this program (in Microsoft Word format).

问题分析：

该问题等价于最优化问题，即现在有N个任务，每个任务需要一个时间区间t_i来处理。每个任务i可以灵活处理，只要在规定的截止时间d_i之间完成处理就行，即任务i在时间段0～d_i -t_i的任意一个时刻，并且要求一个长度为t_i连续的时间区间。虽然如此，但是因为只有一个资源来完成任务，所以不同的任务要求被分在完全不重叠的区间。    在这种情况下，根据想要优化的目标，应该存在许多的优化方法。简单而有效优化方法，考虑一个非常自然的通过贪心算法可以被优化的目标。有几种自然的贪心方法，在这些方法中我考虑任务的数据有(t_i,d_i)，并且按照某种简单的规则对他们排序。

1. 一种方法是把任务按长度t_i增长的次序安排，使得较短的任务尽快结束。但是它完全忽略了任务的截止时间。例如，题目中提供的作业D，完成它所需的时间为1，最短，但是它的截止时间为7，而其他的作业虽然完成他们所需的时间较长，但是截止时间较短。如果要想尽可能多得完成任务，显然安排先完成作业D不巧当，而安排先完成其他的作业比较合适。因此该规则的最优化规则失效。

2. 根据1的分析我们应该可以考虑先完成(d_i-t_i)非常小的任务，这种任务是那种需要用最小松弛时间开始的任务，即先安排完成可调整时间最短的作业。因此将按照d_i-t_i增长的次序对任务排序。但是，这种贪心规则也不是最优的。考虑两个任务的实例，假设有3个任务，他们的截止时间和完成任务所需的时间分别为（1）8和7，（2）4和2，（3）5和3，那么按照2的规则，先选择任务（1），那么最终完成的任务只有任务（1），完成的任务数量也只有1；而选择任务（2）或者（3），那么可以在规定的时间内可以完成任务（2）和（3），完成的任务数量为2.因此该规则也失效。

3. 综合考虑d_i和t_i。因为每个任务只要在它的截止时间之前完成即可，而不需要该什么时候开始，那么要想完成更多的任务，先完成截止时间较短的任务，并放弃已超过截止时间的任务。一般来说，截止时间小的作业暗示着完成该作业所需的时间也少，反之不一定成立。因此要想完成更多的作业，那么需要在作业的截止时间之前一个一个的完成它。总之，优化的思路为：a.在未完成的任务中，选择截止时间较早的任务，记为 i，若完成其所需的时间t_i小于它的截止时间d_i，那么放弃完成该任务，继续a步骤，否则，就选择完成该任务，并且更新剩下未完成任务的截止时间，即将它们的截止时间减去完成前一个任务所需的时间，继续a步骤。根据该规则写出该算法：

i.初始化定义  

  i1. 定义一个2维数组 Task[3][NUMOFTASK]。其中第一行的元素表示任务i的截止时间，第二行的元素表示完成任务i所需时间，第三行表示任务i的代号（因为排序，所以需要记住其任务代号1.. NUMOFTASK）。这里NUMOFTASK表示任务数量。为了简单表示符号，用三个一维数组Task0 [NUMOFTASK] ， Task1 [NUMOFTASK]， Task2[NUMOFTASK]表示 Task[3][NUMOFTASK] 对应的第0、1、2行；   

  i2. 完成任务代号数组FinishedTask[NUMOFTASK],初始化全为0（如果FinishedTask[]数组元素值为任务代号i，表示完成了任务i）。    

  i3. 已完成任务数量SumOfFinishedTask=0.

       a.将所有的任务按照截止时间从小到大排序。若存在截止时间相同的情况，那么进一步按照其对应的完成所需时间从小到大排序。根据第一行排好序为： Task1[0]<= Task1[1]...<= Task1[NUMOFTASK-1](对应的Task1[]、Task2[]对应的元素位置也更改好)。

               b. 按照Task0[]的次序考虑任务i，i从1到NUMOFTASK(或者是0～NUMOFTASK-1)   将Task0[i]与Task1[i]进行比较，    

                    b1.若小于，那么跳过，重复b；    

                    b2.若大于等于，那么执行该任务，并且         

                          b21.将Task2[i]录入以完成任务的数组，同时SumOfFinishedTask加1.         

                          b22.j从i+1到NUMOFTASK（这里表示未完成的任务），              

                                 b221.更新截止时间，即用当前的截止时间减去完成任务i所需要的时间，Task1[j]=Task1[j]-Task2[i]

              c.打印完成任务总数SumOfFinishedTask，并根据它打印出完成的任务的顺序即其代号,结束。

代码实现：

#include <stdio.h>
#define NUMOFTASK 5
void swap(int *a,int *b)
{
    int temp=*a;
    *a=*b;
    *b=temp;
    return;
}
int partition(int *r, int first, int end)
{
    int i=first;
    int j=end;
    while (i<j) 
    {
        while (i<j&&*(r+i)<=*(r+j)) 
        {    
			if(*(r+i)==*(r+j))//如果两者的截止时间相等，那么需要接着比较完成他们所需要的时间
				if(*(r+i+2*NUMOFTASK)>*(r+j+2*NUMOFTASK))
					break;
			j--;
        }
		if(i<j)
        {
            swap((r+i),(r+j));
            swap((r+i)+NUMOFTASK,(r+j)+NUMOFTASK);
			swap((r+i)+2*NUMOFTASK,(r+j)+2*NUMOFTASK);
            i++;
        }
        while (i<j&&*(r+i)<=*(r+j))
		{
			if(*(r+i)==*(r+j))//如果两者的截止时间相等，那么需要接着比较完成他们所需要的时间
				if(*(r+i+2*NUMOFTASK)>*(r+j+2*NUMOFTASK))
					break;
            i++;
        }
		if(i<j)
        {
            swap((r+i),(r+j));
            swap((r+i)+NUMOFTASK,(r+j)+NUMOFTASK);
			swap((r+i)+2*NUMOFTASK,(r+j)+2*NUMOFTASK);
            j--;
        }
    }
    return i;
}
void QuickSort(int *r,int first,int end)
{
    if(first<end)
    {
        int pivot=partition(r, first, end);
        QuickSort(r, first, pivot-1);
        QuickSort(r, pivot+1, end);
    }
}

int main (int argc, const char * argv[])
{
    int DueTime[][NUMOFTASK]={{8,3,3,7,4},{1,2,3,4,5},{5,2,2,1,2}};//DueTime数组元素第一行代表一个任务的截止时间，第二行代表任务的代号,第三行代表完成任务所需的时间，仅供排序用
    int TimeToFinish[NUMOFTASK]={5,2,2,1,2};//TimeToFinish数组元素代表任务所需的时间
    int FinishedTask[NUMOFTASK]={0};//FinishedTask用来表示完成的任务代号，元素值为0表示没没完成任务
    int SumOfFinishedTask=0;//记录完成任务的数量
    //对DueTime数组元素的第一行元素进行快速排序，当DueTime中的截止时间有相同的情况时，按照对应的TimeToFinish元素从小到大排序，
    //如果一个任务的截止时间与完成任务所需的时间一样，那么随机排序
    QuickSort(*DueTime, 0, NUMOFTASK-1);
    int i=0;//老的编译器不支持在for语句中定义变量
    for(i=0;i<NUMOFTASK;i++)
    {
        if(DueTime[0][i]>=TimeToFinish[DueTime[1][i]-1])//截止时间大于等于任务所需时间，那么就可以顺利执行完该任务
        {
            FinishedTask[SumOfFinishedTask++]=DueTime[1][i];
            int j=i+1;
            for(;j<NUMOFTASK;j++)
            {
                DueTime[0][j]=DueTime[0][j]-TimeToFinish[DueTime[1][i]-1];//将剩下的任务的截止时间减下完成前一个任务所花的时间
            }
        }
    }
    //打印出完成的任务数量
    printf("completed:%d tasks!\n",SumOfFinishedTask);
    //打印出完成的任务的顺序即其代号
    for (i=0; i<SumOfFinishedTask; i++) {
        //if(FinishedTask[i]!=0)
        printf("step %d:\tFinished No.%d Task。\n",i+1,FinishedTask[i]);
    }
    return 0;
}

更多详细信息请查看java教程网 http://www.itchm.com/forum-59-1.html