【算法复习二】传统基本算法（迭代、递归、分治）

一，迭代与递推

1）迭代法也称“辗转法”，是一种不断用变量的旧值递推出新值的解决问题的方法。迭代算法一般用于数值计算。迭代法应该是我们早已熟悉的算法策略，程序设计语言课程中所学的累加、累乘都是迭代算法策略的基础应用。例如：斐波那契数列

例子：兔子繁殖问题

一对兔子从出生后第三个月开始，每月生一对小兔子。小兔子到第三个月又开始生下一代小兔子。假若兔子只生不死，一月份抱来一对刚出生的小兔子，问一年中每个月各有多少只兔子。

•问题分析

因为一对兔子从出生后第三个月开始每月生产一对小兔子，则每月新下生的小兔子的对儿数显然由前两个月的小兔子的对儿数决定。则繁殖过程如下：

一月 二月 三月四月 五月 六月……

1 11+1=2 2+1=3 3+2=5 5+3=8 ……

•数学建模（斐波那契数列）

y1=y2=1，yn=yn-1+yn-2，n=3，4，5，……

2）倒推法的概念

•倒推法：是对某些特殊问题所采用的违反通常习惯的，从后向前推解问题的方法。例如，在不知前提条件的情况下，由结果倒过来推解它的前提条件，从而求解问题。又如，由于存储的要求，而必须从后向前进行推算。另外，在对一些问题进行分析或建立数学模型时，从前向后分析问题感到比较棘手，而采用倒推法，则问题容易理解和解决。

例子：穿越沙漠问题

用一辆吉普车穿越1000公里的沙漠。吉普车的总装油量为500加仑，耗油率为1加仑/公里。由于沙漠中没有油库，必须先用这辆车在沙漠中建立临时油库。该吉普车以最少的耗油量穿越沙漠，应在什么地方建油库，以及各处的贮油量。

•问题分析

贮油点问题要求要以最少的耗油量穿越沙漠，即到达终点时，沙漠中的各临时油库和车的装油量均为0。这样只能从终点开始向前倒着推解贮油点和贮油量。

•数学模型

根据耗油量最少目标的分析，下面从后向前分段讨论。

第一段长度为500公里且第一个加油点贮油为500加仑。

第二段中为了贮备油，吉普车在这段的行程必须有往返。

下面讨论怎样走效率高：

1）首先不计方向这段应走奇数次（保证最后向前走）。

2）每次向前行进时吉普车是满载。

3）要能贮存够下一加油点的贮油量，路上耗油又最少。

•综上分析

从终点开始分别间隔 500，500/3，500/5，500/7，……（公里）设立贮油点，直到总距离超过1000公里。每个贮油点的油量为500，1000，1500，……。

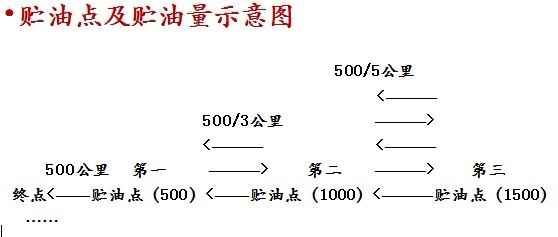
•终极解释：

1）从终点推，到终点必须正好没油，且中途加油站也耗光。所以距离终点500公里有一个500加仑储油点

2）第二个，要想把第一个储油点，储500加仑，最少需要三次，且汽车需要满载油，则距离为500*2 - 3X=500 得距离X=500/3 储油量：500*2=1000

3）第三个，距离计算公式：500*3 -5x =1000 -->x=500/7 储油量：3*500=1500

二，分治与递归

1）分治法在每一层递归上都有三个步骤：

（1）划分：把输入的问题实例划分为若干子问题，尽量使子问题的规模大致相同。

（2）求解：若子问题规模较小而容易被解决则直接解，否则，当问题的规模大于某个预定义的阀值时，求解步骤由个递归调用组成。

（3）合并：将各个子问题的解合并为原问题的解。

分治和递归的关系

分治与递归像一对孪生兄弟，经常同时应用在算法设计之中。因为从分治法的算法框架中可以看出，分治法设计出的算法一般是一个递归过程。

2）二分治的基本思想

在算法设计中每次一个问题分解成的子问题个数一般是固定的，每个子问题的规模也是平均分配的。当每次都将问题分解为原问题规模的一半时，称为二分治法。二分法是分治法较常用的分解策略，数据结构课程中的折半查找、归并排序等算法都是采用此策略实现的。

例题：二分治法求最大、最小值

#include <iostream>
using namespace std;
void FindMaxAndMin(int a[], int begin, int end, int* pmax,int* pmin)
{
	if(end-begin <=1) //递归出口 
	{
		if(a[begin] <= a[end])
 		{
			*pmax = a[end];
			*pmin = a[begin];
			return;
		}
		else
		{
			*pmin = a[end];
			*pmax = a[begin];
			return;
		}
}
	int min1, min2, max1, max2;
	int mid = (begin+end)/2;
	FindMaxAndMin(a, begin, mid, &max1, &min1);
	FindMaxAndMin(a,mid+1, end,&max2, &min2);
	*pmin = min1 < min2 ? min1 : min2;
	*pmax = max1 < max2 ? max2 : max1;
}
int main()
{
	int a[] = {1,2,3,4,5,9,41,8,12,20,98};
	int max,min;
	FindMaxAndMin(a,0,10,&max,&min);
	cout<<"the max num is:"<<max<<"，  the min num is:"<<min<<endl;
	return 0;
}
 

例题：线性时间求数组，第k小元素

• 问题分析

这个问题可以通过排序来解决，最好的排序算法的复杂性是O（n*log(n)），下面我们要利用分治法，找到复杂性为O（n）的算法。但这个问题不能用简单的二分法分解成完全独立、相似的两个子问题。因为在选出分解后第一组的第k小的数据和第二组的第k小的数据，不能保证在这两个数据之一是原问题的解。

• 例如：

求一组数据中的第2小数据：(-2,11,-4,13,-5,-3）

若用二分法将实例中的数据分解为两组(-2,11,-4),（13,-5,-3），第一个子问题的解是-2，第二个子问题的解是-3，两个子问题的解不能简单地得到原问题的解。原问题的解是-4。

• 解决方法

方案一，新建一个k数组，对k数组排序，然后每次将最大数跟余下数组中每一个数比较，“余下数”小则删除k数组中最大，然后将“余下数”插入k数组，遍历到最后，k数组中最大数为所求。

方案二，分治算法求解（******）

#include <iostream>
using namespace std;

class QuickSort
{
private:
	int *arr;//待排序数组
	int length;//数组长度
public:
	//构造函数
	QuickSort(int length)
	{
		arr=new int[length+1];
		this->length=length;
	}
	//交换函数
	void swap(int i,int j)
	{
		int temp=arr[i];
		arr[i]=arr[j];
		arr[j]=temp;
	}
	//输入数据
	void input()
	{
		int i=1;
		cout<<"please input 10 number:"<<endl;
		while(i<=length)
		{
			cin>>arr[i];
			++i;
		}
	}
	//输出函数
	void display()
	{
		int i=1;
		while(i<=length)
		{
			cout<<arr[i]<<" ";
			++i;
		}
		cout<<endl;
	}
	//随机化划分函数
	int randomizedPartition(int start,int end)
	{
		int i=start+rand()%(end-start+1);//产生随机数start~end
		swap(i,start);//交换元素
		return partition(start,end);//返回划分位置
	}

	//划分函数
	int partition(int start,int end)
	{
		int key=arr[start];//arr[start]作为划分关键字
		int i=start;
		int j=end;
		//交换元素
		while(true)
		{
			while(arr[i]<key)
			{
				++i;
			}
			while(arr[j]>key)
			{
				--j;
			}
			//寻找两个可以交换的元素
			//如果j<=i，说明arr[j]在左半域，arr[i]在右半域,划分完成，在j,j+1之间划分
			if(i<j)
			{
				swap(i,j);
				++i;
				--j;
			}
			else
			{
				return j;
			}
		}
	}  
	//快速排序
	void quickSort(int start,int end)
	{
		if(start<end)//起码有2个元素
		{
			int middle;
			middle=randomizedPartition(start,end);
			quickSort(start,middle);
			quickSort(middle+1,end);
		}
	}
	//线性时间选择第k小元素
	int randomizedSelect(int start,int end,int k)
	{
		if(start==end)//如果有两个元素的段被随机化划分之后，则应该有此等式成立，即找到了第K小元素
		{
			return arr[start];
		}
		else
		{
			int middle=randomizedPartition(start,end);
			int left=middle-start+1;
			if(k<=left)//
			{
				return randomizedSelect(start,middle,k);//在划分后的左侧寻找第k小元素
			}
			else
			{
				return randomizedSelect(middle+1,end,k-left);//在划分后的右侧寻找第k-左段长度小的元素
			}
		}
	}
};

int main()
{
	QuickSort test(10);
	test.input();
	test.display();
	cout<<test.randomizedSelect(1,10,3)<<endl;//寻找第3小元素
	test.quickSort(1,10);//随机化快速排序
	test.display();//打印结果
	
	return 0; 
}