【算法复习二】传统基本算法（分治----残缺棋盘问题）

• 问题描述：

残缺棋盘是一个有2k×2k（k≥1）个方格的棋盘，其中恰有一个方格残缺。如图给出k=1时各种可能的残缺棋盘，其中残缺的方格用阴影表示。

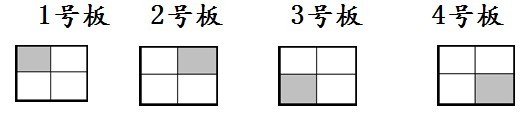
• 残缺棋盘问题就是要用这四种三格板覆盖更大的残缺棋盘。在此覆盖中要求：

1）两个三格板不能重叠

2）三格板不能覆盖残缺方格，但必须覆盖其他所有的方格。

小格子数（2k×2k -1）三格板中小格子数3。所以所需要的三格板总数为(2k×2k -1 )/3。

• 例如，一个4*4的残缺棋盘2k*2k

以k=2时的问题为例，用二分法进行分解，得到的四个k=1的棋盘。但要注意这四个棋盘，并不都是与原问题相似且独立的子问题。

因为当如图中的残缺方格在左上部时，第1个子问题与原问题相似，而右上角、左下角和右下角三个子棋盘（也就是图中标识为2、3、4号子棋盘），并不是原问题的相似子问题，自然也就不能独立求解了。当使用一个①号三格板覆盖2、3、4号三个子棋盘的各一个方格后，我们把覆盖后的方格，也看作是残缺方格（称为“伪”残缺方格），这时的2、3、4号子问题就是独立且与原问题相似的子问题了。

• 问题分析

从以上例子还可以发现

当残缺方格在第1个子棋盘，用①号三格板覆盖其余三个子棋盘的交界方格，可以使另外三个子棋盘转化为独立子问题；

当残缺方格在第2个子棋盘时，则首先用②号三格板进行棋盘覆盖

当残缺方格在第3个子棋盘时，则首先用③号三格板进行棋盘覆盖

当残缺方格在第4个子棋盘时，则首先用④号三格板进行棋盘覆盖，这样就使另外三个子棋盘转化为独立子问题。

程序代码思路：

表示方法：每个三格板需要用同一个数字表示，不同三格板编号不同。

源码：

#include <iostream>
#include <iomanip>
using namespace std;

int board[100][100];  //存放棋盘L型的标号数组；
int tile=1;    // L型骨牌号
void chessBoard(int tr, int tc, int dr, int dc, int size)
{ 
	  if (size==1)
		  return;
      int t = tile++;     // L型骨牌号
	  int s = size/2;     // 分割棋盘
      //________________________________________________ 覆盖左上角子棋盘
      if (dr<tr+s&&dc<tc+s)     // 特殊方格在此棋盘中
		  chessBoard(tr, tc, dr, dc, s);
      else                               // 此棋盘中无特殊方格
	  {           
         board[tr+s-1][tc+s-1]=t; // 用 t 号L型骨牌覆盖右下角
         chessBoard(tr,tc,tr+s-1, tc+s-1, s);// 覆盖其余方格
	  } 
      
	  //________________________________________________ 覆盖右上角子棋盘
      if (dr < tr + s && dc >= tc + s)     // 特殊方格在此棋盘中
		  chessBoard(tr, tc+s, dr, dc, s);
      else                                  // 此棋盘中无特殊方格
	  {
		  board[tr + s - 1][tc + s] = t;   //用t号L型骨牌覆盖左下角
          chessBoard(tr, tc+s, tr+s-1, tc+s, s);// 覆盖其余方格
	  }
     
	 //_______________________________________________ 覆盖左下角子棋盘
      if (dr >= tr + s && dc < tc + s)  // 特殊方格在此棋盘中
		  chessBoard(tr+s, tc, dr, dc, s);
      else                               // 此棋盘中无特殊方格                       
	  {
         board[tr + s][tc + s - 1] = t;  // 用 t 号L型骨牌覆盖右上角
        chessBoard(tr+s, tc, tr+s, tc+s-1, s);// 覆盖其余方格
	  } 
      
	  //__________________________________________________ 覆盖右下角子棋盘
      if (dr >= tr + s && dc >= tc + s)  // 特殊方格在此棋盘中
		  chessBoard(tr+s, tc+s, dr, dc, s);
      else 
	  {
         board[tr + s][tc + s] = t;     // 用 t 号L型骨牌覆盖左上角       
         chessBoard(tr+s, tc+s, tr+s, tc+s, s); // 覆盖其余方格
	  }
}
int main()
{

	int size,dr,dc;
	cout<<"\t\t\t棋盘覆盖问题\n";
	cout<<"2^k×2^k 个方格变长size(size=2,4,8,16,32,64)：";
	cin>>size;
	cout<<"分别输入特殊块的行下标dr,列下标dc(0-"<<(size-1)<<"):";
	cin>>dr>>dc;
	board[dr][dc]=0;
	cout<<"棋盘覆盖图：\n";
	chessBoard(0, 0, dr, dc, size);
	
	int i,j;
	for( i=0;i<size;i++)
	{
		for( j=0;j<size;j++)
			cout<<setw(6)<<board[i][j];//setw(6)//输出量不足6个字符时在左面填充空白 
		cout<<endl<<endl;
	}
	return 0;
}

分治递归执行步骤：

1）chessBoard(0, 0, 0, 0, 4);

{ t=1; s=2;

chessBoard(0, 0, 0, 0, 2);

{ t=2; s=1;

chessBoard(0, 0, 0, 0, 1);

{ s==1

return

}

以下三步

将左上角 三格板 用t=2覆盖

}

return

以下三步 对右上递归 先 用t=1 覆盖左下

左下递归 先 用t=1 覆盖右上

右下递归 先 用t=1 覆盖左上

递归处理类似。

}