【算法复习三】算法设计技巧与优化----算法设计技巧

一，例题：找出n个自然数(1,2,3,…,n)中r个数的组合。

•例如，当n=５,r=3时，所有组合为：

12 3 1 2 4

12 5 13 4

13 5 14 5

23 4 23 5

24 5 34 5

total=10 {组合的总数}

•算法设计

1）n个数中r的组合，其中每r个数中，数不能相同；

2）任何两组组合的数，所包含的数也不应相同。例如，５、４、３与３、４、５。为此，约定前一个数应小于后一个数。将上述两条作为约束条件；

3）当r=3时，可用三重循环进行枚举。

【解法一】穷举法

#include <iostream>
using namespace std;
int main()
{
	int n=6;
	int t=0; 
	for(int i=1;i<n;++i)
	{
		for(int j=i+1;j<n;++j)
		{
			for(int k=j+1;k<n;++k)
			{
				t++;
				cout<<i<<"  "<<j<<"  "<<k<<"  "<<endl;
			}	
		}
	}
	
	cout<<"total: "<<t<<endl;
}

【解法二】穷举中加入限界（第一个输出的最多是3，第二个最多是4，第三个最多5）

#include <iostream>
using namespace std;
int main()
{
	int n=5;
	int r=3;
	int t=0; 
	for(int i=1;i<=3;++i)
	{
		for(int j=i+1;j<=4;++j)
		{
			for(int k=j+1;k<=5;++k)
			{
				t++;
				cout<<i<<"  "<<j<<"  "<<k<<"  "<<endl;
			}	
		}
	}
	
	cout<<"total: "<<t<<endl;
}<span style="color: #c00000;">
</span>

【解法三】递归法求解

在循环算法设计中，对n=5的实例，每个组合中的数据从小到大排列或从大到小排列一样可以设计出相应的算法。但用递归思想进行设计时，每个组合中的数据从大到小排列却是必须的；因为递归算法设计是要找出大规模问题与小规模问题之间的关系。

•分析n=5,r=3时的10组组合数。

1）首先固定第一个数５，其后就是n=4,r=2的组合数，共6个组合。

2）其次固定第一个数4，其后就是n=3,r=2的组合数，共3个组合。

3）最后固定第一个数3，其后就是n=2,r=2的组合数，共1个组合。

至此找到了“５个数中３个数的组合”与“４个数中２个数的组合、3个数中２个数的组合、2个数中２个数的组合”的递归关系。

算法：（两种递归写法）

#include <iostream>
using namespace std;
int a[100]; 
void comb(int m,int k) 
{ 
	int i,j; 
  	for (i=m;i>=k;i--) //循环的关键
  	{ 
    	a[k]=i; 
    	if (k>1) 
           comb(i-1,k-1); 
        else 
        { 
	   		for (j=1;a[j]>0;j++) 
               cout<<a[j]<<" "; 
       	   
       	    cout<<endl;
		}
	}
}
void   com(int   n,   int   r) 
{ 
	int   num=r; 
	int   i=0; 
	for(i=n;i>=r;i--) 
	{ 
		a[r]=i; 
		if(r==1) 
		{ 
			int   j=0; 
			for(j=1;a[j]>0;j++) 
				printf( "%d   ",a[j]); 
                   printf( "\n "); 
             continue; 
        } 
       else 
          com(i-1,r-1);   //应该这样写 
          //com(n-1,r-1);//这样会造成每次重复取数，是错误的                                                  
} 
} 
int main()
{
	comb(5,3);
	return 0;
}

【解法四】回溯法求解

#include <iostream>
using namespace std;
int a[100]; 

void   comb_back(int   m,int   r) 
{
	int   i,j,k=0; 
    i=0,a[i]=1; 
	do{ 
        if(a[i]-i <=m-r+1)
		{   
  			if(i==r-1)
  			{   //已找到一个组合 
				printf( "第%d组： ",++k); 
    			for(j=0;j <r;j++)
					printf( "%d ",a[j]);printf( "\n "); 
      			a[i]++;                   
        		continue;
			} 

			i++;   //向前试探 
   			a[i]=a[i-1]+1;
         } 
     	else
		{//回溯 
  			if(i==0)   
				return;//已找到了全部解 
    		a[--i]++;
		} 
	}while(1); 
}
int   main() 
{ 
	comb_back(5,3); 
	return   0; 
} <span style="color: #c00000;">
</span>

二，例题：警察局抓了a，b，c，d四名偷窃嫌疑犯，其中只有一人是小偷。审问中

a说：“我不是小偷。”
b说：“c是小偷。”
c说：“小偷肯定是d。”
d说：“c在冤枉人。”
现在已经知道四个人中三人说的是真话，一人说的是假话，问到底谁是小偷？

•算法设计

将a,b,c,d将四个人进行编号，号码分别为1，2，3，4。则问题可用枚举尝试法来解决。

用变量x存放小偷的编号，则x的取值范围从1取到4，就假设了他们中的某人是小偷的所有情况。四个人所说的话就可以分别写成：

a说的话：x！=1

b说的话：x==3

c说的话：x==4

d说的话：x！=4

源码：

#include <iostream>
using namespace std;
int main( )
{   
  for(int x=1;x<=4;x++)
   {
    	if((x!=1)+(x==3)+(x==4)+(x!=4)==3)
            cout<<char(64+x)<<" is a thief";
        
   } 
   return 0;
 }

三，例题：循环赛日程编排

• 问题定义

设有n=2k个运动员进行的单循环赛，要求设计一个满足一下条件的比赛日程表：

1、每个选手必须与其他n-1个选手各赛一次；

2、每个选手一天只能参赛一次；

3、循环赛在n-1天内结束。

• 二分治策略递归算法

将所有选手分为两半，则n个选手的比赛日程表可以通过n/2个选手的比赛日程表来决定，递归的进行二分治划分，直到只剩下两个选手时，比赛日程表的制定就很简单了。

时间复杂度为O(n`2)。

• 递归算法1设计

递归函数dimidiata(intI,intj,int n)

i—起始行号

j—终止行号

n—问题规模

用二分治分解二维表，可分解出左上、左下、右上、右下4个部分。

算法的递归方程为：T(n)=2T(n/2)+O(n2/2)

算法的空间复杂度：3*k个整型栈辅助空间。

时间复杂度为：O(n`2)。

• 算法4—二维递推算法

分析数据，找出递推关系：n=8为例。

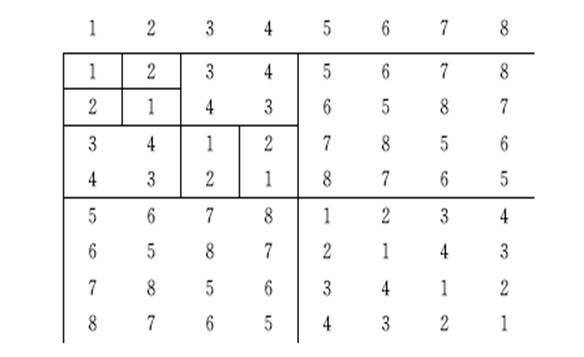
分析如下：

1、先做出规模为1的问题的解，即左上角的1*1的方阵，递推规模为k=2`0、2`1、2`2(2*2)…的方阵。

2、左下角新增加的每一行列的数据是其“对应行列”数据+规模/2。

“对应行列”的含义：

行号=当前行号–规模/2

列号=当前列号

3、右上角与左下角数据一样。

“对应行列”的含义：

列号=当前列号–规模/2

行号=当前行号

4、右下角与左上角数据一样。

“对应行列”的含义：

行号=当前行号–规模/2，列号=当前列号

或

列号=当前列号–规模/2，行号=当前行号

• 算法4分析

时间复杂度为O(n2)。

算法

#include <iostream>
using namespace std;
#define N 8
int table[N][N];
void copytable(int x1,int y1,int x2,int y2,int n)
{
	int i,j;
	for(i=0;i<n;i++)
   		for(j=0;j<n;j++)
    		table[x2+i][y2+j]=table[x1+i][y1+j];
}
void copytableadd(int x,int y,int n)
{
    int i,j;
	for(i=0;i<n;i++)
   		for(j=0;j<n;j++)
   		{
    		table[i][j+n]=table[i][j]+n;
   		}
}
void maketable(int x,int y,int n)
{
	if(n==2)
	{
   		return;
	}
	else
	{
   		n=n/2;
   		maketable(0,0,n);
   		copytableadd(0,n,n);
   		copytable(0,0,n,n,n);//拷贝右下角 
   		copytable(0,n,n,0,n);//拷贝左下角 
	}
}
int main()
{
	int i,j;
	table[0][0]=1;
	table[0][1]=2;
	table[1][0]=2;
	table[1][1]=1;
	maketable(0,0,N);
	for(i=0;i<N;i++)
	{
  		 for(j=0;j<N;j++)
    		cout<<table[i][j]<<" ";
   		cout<<endl;
	}
	cin>>i;
	return 0;
}

如果队伍数为奇数算法

#include<stdio.h>
#define MAXSIZA 32			//最大参赛队伍个数
int main()
{
	int m,n,i;
	int a[MAXSIZA][MAXSIZA];		//用于日程表存储
	//输入处理
	printf("请输入参赛队伍个数（2-%d）：",MAXSIZA);
	scanf("%d",&m);
	while(m>MAXSIZA || m<2)
	{
		printf("输入数据有误，请重新输入参赛队伍个数（2-%d）：",MAXSIZA);
		scanf("%d",&m);
	}
	//奇数个选手，虚拟一个选手，使之成为偶数
	n=m+m%2;
	//给选手编号，存储在数组第一列
	for(i=0;i<n;i++)
		a[i][0]=i+1;
	//生成日程表，将比赛安排存储在数组中
	for(i=1;i<n;i++)
	{
		for(int j=0;j<n/2;j++)
		{
			a[a[j][0]-1][i]=a[(n-1-j)%n][0];
			a[a[(n-1-j)%n][0]-1][i]=a[j][0];
		}
		//将数组第一列按将除n外的选手按顺时针（或逆时针旋转）n/2-1个位置		  
		int k=0,t;t=a[k][0];
		for(;k<n-2;k++)
			a[(k*(n/2-1))%(n-1)][0]=a[(k+1)*(n/2-1)%(n-1)][0];
		a[(k*(n/2-1))%(n-1)][0]=t;
	}
	for(i=0;i<n;i++)		//输出表头
	{
		if(i==0)printf("队号\t");
		else
			printf("第%d天\t",i);
	}
	printf("\n"); 
	for(i=0;i<m;i++)			//输出日程表
	{
		for(int j=0;j<n;j++)
		{
			if(m!=n && a[i][j]==n)			//用输出'-'表示轮空
				printf("  -\t");
			else
				printf("  %d\t",a[i][j]);
		}
		printf("\n");
	}
	
	return 0;
}