一,组合数学问题
1)排列定义
• 从n个不同的元素中,取r个不重复的元素,按次序排列,称为从n个中取r个的无重排列。
•排列的全体组成的集合用P(n,r)表示。当r=n时称为全排列。
组合定义
• 定义从n个不同元素中取r个不重复的元素组成一个子集,而不考虑其元素的顺序,称为从n个中取r个的无重组合。
• 组合的全体组成的集合用C(n,r)表示。
2)例题一:某车站有6个入口处,每个入口处每次只能进一人,一组9个人进站的方案有多少?
【解法】一进站方案表示成:
00011001010100
其中“0”表示人,“1”表示门框,其中“0”是不同元,“1”是相同元。给“1”n个门只用n-1个门框。任意进站方案可表示成上面14个元素的一个排列。
[解法1]
分析:第一个人可以有6种进站的方式,也就是从6个入口的任意一个站进站,那么第二个人也可以有6种选择入口的方法,但是假如他和第一个人选择的入口是相同的话,就有谁在前的情况,所以第二个人就有了7种进站方案;同理,第三个人进站的话就有8种进站方案,这样算下去,那么第九个人就有14种进站的方法。
故所求方案为 14!/5!=6×7×8×...×14=726485720
[解法2]
在14个元的排列中先确定“1”的位置,有C(14,5)种选择,在确定人的位置,有9!种选择。
故 C(14,5)*9! 即所求:14!/5!
注意:C(14,5)= (14! - (14-5)!)/ 5!
如:a10 a3
a40 a6 a70
a9 a100 a120
a14
方案为(2,5,8,11,13)
例题二:简单格路径数问题 (类腾讯笔试题)
从 (0,0)点出发沿x轴或y轴的正方向每步走一个单位,最终走到(m,n)点,有多少条路径?
【分析】• 无论怎样走法,在x方向上总共走m步,在y方向上总共走n步。若用一个x表示x方向上的一步,一个字母y表示y方向上的一步。
• 则(0,0)→(m,n)的每一条路径可表示为m个x与n个y的一个有重排列。将每一个有重排列的x与y分别编号,可得m!*n!个m+n元的无重全排列。
【分析】向上可以走m步,向右可以走n步。注意,必须向上走m步,向右走n步才能到达(m,n)
只需要考虑上和右依次在哪里出现,所以不难得出答案 C(m+n,n)=C(m+n,m)
3)容斥原理
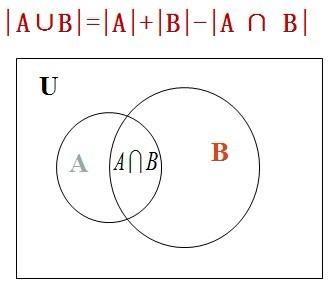
•最简单的计数问题是求有限集合A和B的并的元素数目。显然有
• 定理:即具有性质A或B的元素的个数等于具有性质A和B的元素个数。
求a,b,c,d,e,f六个字母的全排列中不允许出现ace和df图象的排列数。
解:设A为ace作为一个元素出现的排列集,B为df作为一个元素出现的排列集,
A∩B为同时出现ace、df的排列数。
•
|A|=4!|B|=5! |A∩B|=3!
|A∩B|= 6!- (5!+4!)+3!=582
4)容斥与鸽巢原理
鸽巢原理之一:鸽巢原理是组合数学中最简单也是最基本的原理,也叫抽屉原理。即“若有n个鸽子巢,n+1个鸽子,则至少有一个巢内有至少有两个鸽子。”
• 367人中至少有2人的生日相同。
• 10双手套中任取11只,其中至少有两只是完整配对的。
• 参加一会议的人中至少有2人认识的别的参加者的人数相等。
鸽巢原理之二:m1 , m2 , … , mn都是正整数,并有m1 + m2 +… +mn-n + 1个鸽子住进n个鸽巢,则至少对某个 i有第 i个巢中至少有mi个鸽子,i = 1 , 2 , … , n.
•显然,鸽巢原理之一是鸽巢原理之二的特殊情况,即m1 = m2 = … = mn= 2,如若不然,则对任意 i, 都有第i个巢中的鸽子数≤mi-1 则,鸽子总数≤ m1 + m2 +… +mn-n,与假设相矛盾.
例题一:拉蒙赛(Ramsey)问题
6 个人中至少存在3人相互认识或者相互不认识
•证:这个问题与凸六边形完全图的内边着二色,存在同色三角形等价.假定用红蓝着色.
• 设凸六边形完全图的顶点集为{v1,
v2 , ··· , v6 },dr(v)表示与顶点v
关联的红色边的条数,db(v)表示与v
关联的蓝色边的条数.在凸六边形完全图中,有dr(v)+db(v)=5,由鸽巢原理可知,至少有3条边同色.
例题二:拉丁方
•有1,2,3..,n构成的n╳n方阵,(aij)n╳n
要求:每行每列1,2,3..,n各出现一次。称为拉丁方。

二,生成函数
生成函数定义
•
对于序列a0,a1,a2,a3,a4……构造一函数:G(x) = a0 + a1x + a2x`2 + ……称函数G(x)是序列a0,a1,a2,a3,a4……的生成函数。
•例如:(1+x)`n是C(n,0),C(n,1),C(n,2)……C(n,n)的生成函数。
•如若已知序列a0,a1,a2,a3,a4……则对应的生成函数G(x)便可根据定义给出。反之亦然。
例题:由红球两个,白球、黄球各一个,试求有多少种不同的组合方案
一个球:3
二个球:4
三个球:3
四个球:1 总共:12种
三,指数型生成函数
指数型生成函数的概念
•设有n个元素,其中元素a1重复了n1
次,元素a2重复了n2 次,…,ak重复了nk次,从中取r个排列,求不同的排列数.
• 如果n1 = n2 = n3 = …… nk = 1,则是一般的排列问题。
现在由于出现重复,故不同的排列计数便比较复杂。先考虑n个元素的全排列,若n个元素没有完全一样的元素,则应有n!种排列。若考虑ni
个元素ai 的全排列数为ni!,则真正不同的排列数为
n! /(n1!*n2!*……nk!)
分享到:



相关推荐
### 巴斯著《计算机算法—设计与分析导论》知识点提炼 #### 一、算法的概念及重要性 - **算法定义**:算法是非正式的一套清晰简单的指令集合,能够解决特定的问题或计算特定的函数。 - **算法的可解性**:如果一个...
接着,第十三和十四章转向整数规划,特别是Gorory的割平面算法,将整数规划与图论有效结合,展示了组合最优化与复杂性理论在实际问题中的应用。 书中的后半部分更多地涉及NP完全性理论。与传统依赖图灵机理论的阐述...
本篇复习资料涵盖了广东工业大学课程“算法设计与分析基础”中的一些关键知识点,它们是期末考试的复习重点。 ### 第二章 算法效率分析基础 在算法效率分析中,我们通常使用大O表示法来描述算法的时间复杂度。例如...
可计算性与计算复杂性是计算机科学中的核心理论领域,主要研究的是问题的解决可能性以及所需资源的量度。这两个概念对于理解计算机系统的局限性和优化算法有着至关重要的作用。 首先,我们来了解一下“可计算性”。...
在计算机科学中,它具有极其重要的地位,因为很多算法设计和复杂性分析都离不开组合数学的理论支持。杨振生教授的课程可能深入浅出地介绍了这一领域的核心概念和算法。 首先,我们要理解基础概念。组合数学主要包括...
组合数学的算法与分析不仅涉及数学理论,还包括对应的算法实现,以及对算法效率的深入探讨。本知识点将梳理组合数学的一些核心算法和理论,以及它们在不同领域的应用。 首先,基本的计数原理是组合数学的核心内容。...
### 知识点详解:“算法-最优化和复杂性” #### 一、最优化理论 最优化是指在特定约束条件下,寻找目标函数的最佳值的过程。这个目标函数通常用于量化某个性能指标,比如最大化利润或最小化成本。在IT领域,最优化...
第十一章 组合优化算法与计算的时间复杂度理论 11.1 dijkstra算法 11.2 floyd算法 11.3 kruskal算法 11.4 求最优树的破圈法和统观法 11.5 二分图中最大匹配与最佳匹配的算法 11.6 fleury算法 11.7 ...
计算机算法设计与分析总复习-PPT.ppt
移动笔试知识点之--计算机类-数据结构与算法分析练习题.pdf 移动笔试知识点之--计算机类-数据结构与算法知识点总结.pdf 移动笔试知识点之--计算机类-计算机组成与体系结构总结.pdf 移动笔试知识点之--计算机类-...
计算机算法设计与分析第2~4章算法复习题 本文将详细解释计算机算法设计与分析第2~4章的相关知识点,并对给定的文件内容进行详细分析。 分治算法 分治算法是一种常用的算法设计策略,它将问题分解为子问题,然后...
计算机-算法分析与设计复习资料 本资源摘要信息是关于算法分析与设计的复习资料,涵盖了算法分析与设计的基本概念、方法和技术。该资源包括填空题、简答题、选择题等多种形式的题目,涵盖了算法分析与设计的各个...
课程主要讨论和介绍计算机算法的复杂性理论,结合对一些熟悉的算法进行分析和总结,强化基础理论知识,对一些大型工程软件的分析,会有一定的辅助作用。它主要介绍计算机科学及应用领域常见的有代表性的非数值算法及...
从给定的文件信息中,我们可以提炼出一系列关于算法与复杂性的关键知识点: ### 基本概念 - **问题、实例与规模**:在算法分析中,问题是指需要解决的任务,实例是问题的具体表现形式,而规模通常指的是实例的大小...
### 东南大学算法设计与分析复习题解析 #### 基本概念 1. **基本运算**:在解决特定问题时,通常会有一种或偶尔两种运算占据主导地位,这些运算称为基本运算。当我们评估算法效率时,主要是关注这些基本运算的执行...
算法设计与分析是计算机科学的基础,旨在创建高效、清晰的算法,并研究其性能和效率。 1. **算法概念** - 算法不仅仅是一串计算机指令,它是程序的灵魂,提供了解决问题的逻辑流程。 - 算法的五个基本特征包括:...
《计算机算法设计与分析》是计算机科学领域的一门核心课程,它主要研究如何高效地解决计算问题,并对算法的效率进行理论分析。这门课程在国科大由刘玉贵老师讲授,涵盖了大量的理论知识和实践应用。刘玉贵老师的讲义...