【组合数学】卡特兰数

关于扩展的卡特兰数：
1.(n-m+1)/(n+1)*c(n+m,n)
2.c[n+m][n]-c[n+m][m-1]
Catalan，Eugene，Charles，卡特兰（1814～1894）比利时数学家，生于布鲁日（Brugge），早年在巴黎综合工科学校就读。1856年任列日（Liege）大学数学教授，并被选为比利时布鲁塞尔科学院院士。

卡特兰一生共发表200多种数学各领域的论著。在微分几何中，他证明了下述所谓的卡特兰定理：当一个直纹曲线是平面和一般的螺旋面时，他只能是实的极小曲面。他还和雅可比（Jacobi，C·G·J）同时解决了多重积分的变量替换问题，建立了有关的公式。

1842年，他提出了一种猜想：方程x^z－y^t＝1没有大于1的正整数解，除非平凡情形3²－2³＝1。这一问题至今尚未解决。

（mathoe注：即除了8、9这两个连续正整数都是正整数的方幂外，没有其他。1962年我国数学家柯召以极其精湛的方法证明了不存在三个连续正整数，它们都是正整数的方幂，以及方程x²－yⁿ＝1，n＞1，xy≠0无正整数解。并且还证明了如果卡特兰猜想不成立，其最小的反例也得大于10¹⁶。）

此外，卡特兰还在函数论、伯努利数和其他领域也做出了一定的贡献。

卡特兰通过解决凸n边形的剖分得到了数列C_n。

凸n＋2边形用其n－1条对角线把此凸n＋2边形分割为互不重叠的三角形，这种分法的总数为C_n。

为纪念卡特兰，人们使用“卡特兰数”来命名这一数列。

据说有几十种看上去毫不相干的组合计数问题的最终表达式都是卡特兰数的形式。

卡特兰数在数学竞赛、信息学竞赛、组合数学、计算机编程等都会有其不同侧面的介绍。

前几个卡特兰数：规定C₀＝1，而

C₁＝1，C₂＝2，C₃＝5，C₄＝14，C₅＝42，

C₆＝132，C₇＝429，C₈＝1430，C₉＝4862，C₁₀＝16796，

C₁₁＝58786，C₁₂＝208012，C₁₃＝742900，C₁₄＝2674440，C₁₅＝9694845。

递推公式

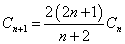
圆周上有标号为1，2，3，4，……，2n的共计2n个点，这2n个点配对可连成n条弦，且这些弦两两不相交的方式数为卡特兰数C_n。

2003年浙江省小学数学夏令营竞赛考了这个题：圆周上10个点可以连成既不相交，也没有公共端点的5条线段，不同的连法共有_____种。

答：方法的种数是卡特兰数C₅＝42，此题被收录进单墫主编的知识出版社出版的《华数奥赛强化训练》小学六年级册的“计数问题”专题。

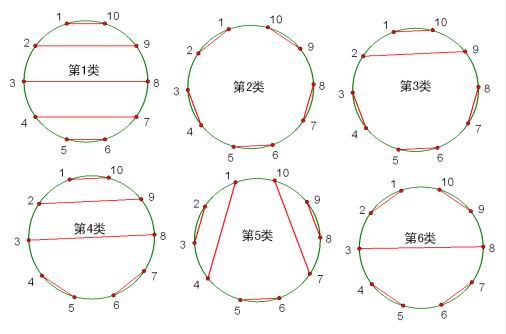
共六种类型，第1类有5种连法，第2类有2种连法，第3类有10种连法，第4类有10种连法，第5类有10种连法，第6类有5种连法。共有42种连法。

1994年《小学数学》有奖征答竞赛：游乐园门票1元一张，每人限购一张。现在有10个小朋友排队购票，其中5个小朋友每人只有1元的钞票一张，另5个小朋友每人只有2元的钞票一张，售票员没有准备零钱。问：有多少种排队方法，使售票员总能找的开零钱？

（此题也被许多奥数资料收录为例题或习题，《华罗庚学校数学课本》小学六年级册的思维训练也收有此题）

答：现把拿1元的5个小朋友看成是相同的，把拿2元的5个小朋友也看成是相同的，使用我们常用的“逐点累加法”：

图中每条小横段表示拿1元的小朋友，每条小竖段表示拿2元的小朋友，要求从A走到B的过程中网格中任何点均有横段数不小于竖段数：拿1元的要先，且人数不能少于拿2元的，即不能越过对角线AB：每个点所标的数即为从A走到此点的方法数。求从A到B的走法的方法数。逐点累加可求出为42，即卡特兰数C₅＝42。

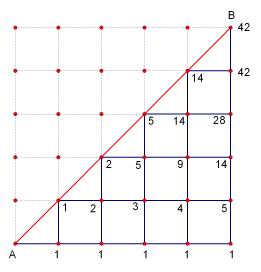
又由于每个小朋友是不相同的，所以共有42×5！×5！＝42×120×120＝604800种情况。

若把此题的10个人，拿1元的有5人，拿2元的有5人改为共有2n个人，拿1元的n人，拿2元的n人，则符合要求的排队方法数为：

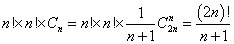
再一个卡特兰数的例子：

甲乙两人比赛乒乓球，最后结果为20∶20，问比赛过程中甲始终领先乙的计分情形的种数。

即甲在得到1分到19分的过程中始终领先乙，其种数是卡特兰数

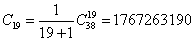
再一个卡特兰数的例子

饭后，姐姐洗碗，妹妹把姐姐洗过的碗一个一个放进碗橱摞成一摞。一共有n个不同的碗，洗前也是摞成一摞的，也许因为小妹贪玩而使碗拿进碗橱不及时，姐姐则把洗过的碗摞在旁边，问：小妹摞起的碗有多少种可能的方式？

答：得数是第n个卡特兰数C_n。

再一个卡特兰数的例子

一个汽车队在狭窄的路面上行驶，不得超车，但可以进入一个死胡同去加油，然后再插队行驶，共有n辆汽车，问共有多少种不同的方式使得车队开出城去？

答：得数是第n个卡特兰数C_n。

卡特兰数

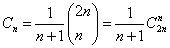
求证：卡特兰数C_n是整数。

证明：

①取整函数不等式：对任意实数x，y有[x＋y]≥[x]＋[y]。这里[x]表示不大于实数x的最大整数。

解：由定义x≥[x]……（1）

y≥[y]……（2）以上两式相加，得：x＋y≥[x]＋[y]，

把上式再取整，得：[x＋y]≥[[x]＋[y]]＝[x]＋[y]，即[x＋y]≥[x]＋[y]。

②1000！的末尾0的个数249个。（现在有的小学奥数书上出现了100！末尾有几个零的题目：24个）

解：1000÷5＝200，

200÷5＝40，

40÷5＝8，

8÷5＝1……3

以上各商相加，即得1000！末尾0的个数＝200＋40＋8＋1＝249个。

③n！的质因数分解式中质因子p的幂次数：

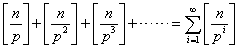…………（1）

k！的质因数分解式中质因子p的幂次数

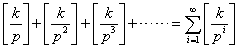…………（2）

(n－k)!的质因数分解式中质因子p的幂次数

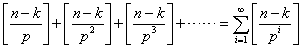…………（3）

这里写成西格马求和式时使用了无穷的形式，但是从某一确定项之后的每项都是0，为了统一，都写成了“∞”形式。

④组合数是整数

解：

⑤卡特兰数是整数

⑥卡特兰数是整数的另外一个证明

④组合数是整数

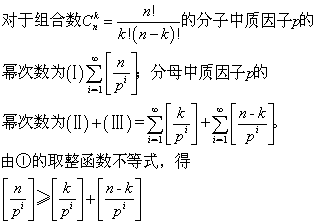
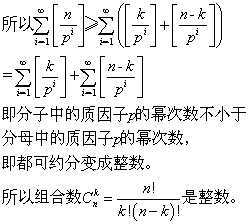
⑤卡特兰数是整数

⑥卡特兰数是整数的另一个证明

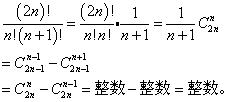
凸六边形剖分成三角形的14种方法，是卡特兰数C₄

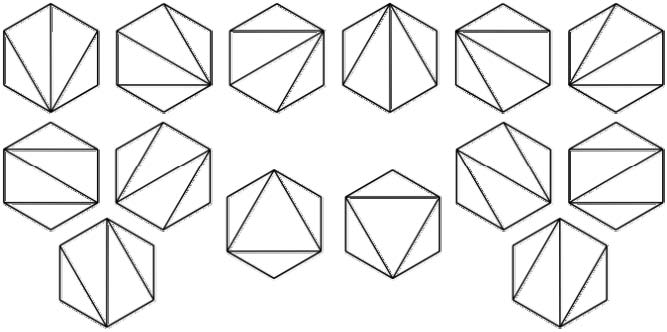
从左下角（0，0）走到右上角（4，4），只允许向上、向右走，但不允许穿过对角线的方法数是14种，是卡特兰数C₄

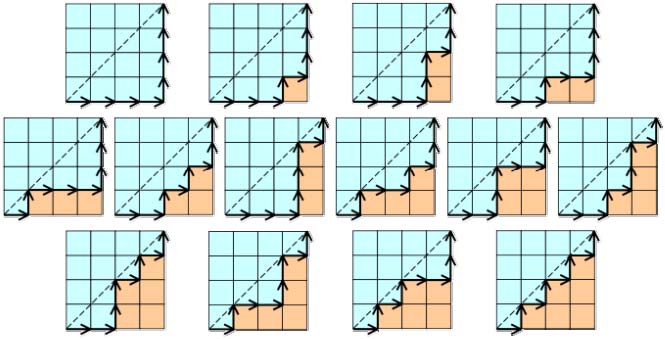
1936第40届匈牙利奥林匹克数学竞赛第1题考了Catalan恒等式的证明。

1979第21届国际数学奥林匹克第1题考了一个卡特兰恒等式的应用的题目






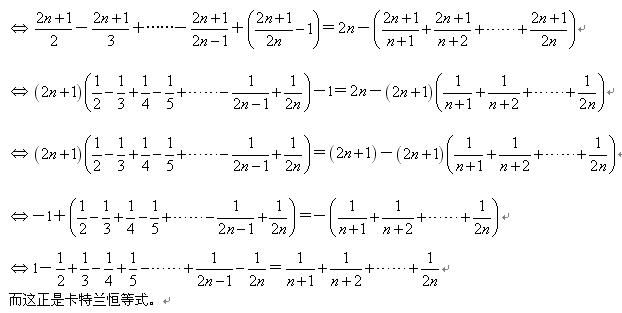
此题由1989年第1届匈牙利-以色列数学竞赛题改编。