ç²¾é€ڑه…«ه¤§وژ’ه؛ڈç®—و³•ç³»هˆ—ï¼ڑن؛Œم€په †وژ’ه؛ڈç®—و³•
ن½œè€…:July م€پن؛Œé›¶ن¸€ن¸€ه¹´ن؛Œوœˆن؛Œهچپو—¥
وœ¬و–‡هڈ‚考ï¼ڑIntroduction To Algorithms,second editionم€‚
-------------------
و¤ç²¾é€ڑوژ’ه؛ڈç®—و³•ç³»هˆ—,ه‰چن¸€èٹ‚,ه·²è®²è؟‡ن؛†ن¸€م€په؟«é€ںوژ’ه؛ڈç®—و³•ï¼Œه…¶ن¸ï¼Œه؟«é€ںوژ’ه؛ڈو¯ڈن¸€è¶ںو¯”较用و—¶O(n),è¦پè؟›è،Œlgnو¬،و¯”较,و‰چوœ€ç»ˆه®Œوˆگو•´ن¸ھوژ’ه؛ڈم€‚و‰€ن»¥ه؟«وژ’çڑ„ه¤چو‚ه؛¦و‰چن¸؛O(n*lgn)م€‚而وœ¬èٹ‚,وˆ‘ن»¬è¦پ讲çڑ„وک¯ه †وژ’ه؛ڈç®—و³•م€‚وچ®وˆ‘و‰€çں¥ï¼Œè¦پçœںو£ه½»ه؛•è®¤è¯†ن¸€ن¸ھç®—و³•ï¼Œوœ€ه¥½وک¯هژ»وں¥و‰¾و¤ç®—و³•çڑ„هژںهڈ‘وکژ者çڑ„è®؛و–‡وˆ–相ه…³و–‡çŒ®م€‚
ok,و¤èٹ‚,ه’±ن»¬ه¼€ه§‹هگ§م€‚
ن¸€م€په †وژ’ه؛ڈç®—و³•çڑ„هں؛وœ¬ç‰¹و€§
و—¶é—´ه¤چو‚ه؛¦ï¼ڑO(nlgn)...
//ç‰هگŒن؛ژه½’ه¹¶وژ’ه؛ڈ
وœ€هڈï¼ڑO(nlgn)
ç©؛é—´ه¤چو‚ه؛¦ï¼ڑO(1).
ن¸چ稳ه®ڑم€‚
ن؛Œم€په †ن¸ژوœ€ه¤§ه †çڑ„ه»؛ç«‹
è¦پن»‹ç»چه †وژ’ه؛ڈç®—و³•ï¼Œه’±ن»¬ه¾—ه…ˆن»ژن»‹ç»چه †ه¼€ه§‹ï¼Œç„¶هگژهˆ°ه»؛ç«‹وœ€ه¤§ه †ï¼Œوœ€هگژو‰چ讲هˆ°ه †وژ’ه؛ڈç®—و³•م€‚
ه †çڑ„ن»‹ç»چ
ه¦‚ن¸‹ه›¾ï¼Œ
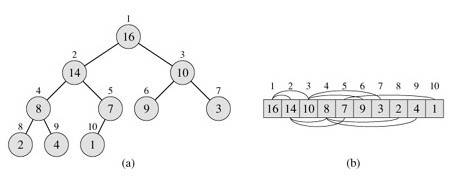
a),ه°±وک¯ن¸€ن¸ھه †ï¼Œه®ƒهڈ¯ن»¥è¢«è§†ن¸؛ن¸€و£µه®Œه…¨ن؛Œهڈ‰و ‘م€‚
و¯ڈن¸ھه †ه¯¹ه؛”ن؛ژن¸€ن¸ھو•°ç»„b),هپ‡è®¾ن¸€ن¸ھه †çڑ„و•°ç»„A,
وˆ‘ن»¬ç”¨length[A]è،¨è؟°و•°ç»„ن¸çڑ„ه…ƒç´ ن¸ھو•°ï¼Œheap-size[A]è،¨ç¤؛وœ¬è؛«هکو”¾هœ¨Aن¸çڑ„ه †çڑ„ه…ƒç´ ن¸ھو•°م€‚
ه½“然,ه°±وœ‰ï¼Œheap-size[A]<=length[A]م€‚
و ‘çڑ„و ¹ن¸؛A[1],iè،¨ç¤؛وںگن¸€ç»“点çڑ„ن¸‹و ‡ï¼Œ
هˆ™çˆ¶ç»“点ن¸؛PARENT(i),ه·¦ه„؟هگLEFT[i],هڈ³ه„؟هگRIGHT[i]çڑ„ه…³ç³»ه¦‚ن¸‹ï¼ڑ
PARENT(i)
return |_i/2_|
LEFT(i)
return 2i
RIGHT(i)
return 2i + 1
ن؛Œهڈ‰ه †و ¹وچ®و ¹ç»“点ن¸ژه…¶هگ结点çڑ„ه¤§ه°ڈو¯”较ه…³ç³»ï¼Œهˆ†ن¸؛وœ€ه¤§ه †ه’Œوœ€ه°ڈه †م€‚
وœ€ه¤§ه †ï¼ڑ
و ¹ن»¥ه¤–çڑ„و¯ڈن¸ھ结点i都ن¸چه¤§ن؛ژه…¶و ¹ç»“点,هچ³و ¹ن¸؛وœ€ه¤§ه…ƒç´ ,هœ¨é،¶ç«¯ï¼Œوœ‰
A[PARENT(i)] ≥ A[i] ,
وœ€ه°ڈه †ï¼ڑ
و ¹ن»¥ه¤–çڑ„و¯ڈن¸ھ结点i都ن¸چه°ڈن؛ژه…¶و ¹ç»“点,هچ³و ¹ن¸؛وœ€ه°ڈه…ƒç´ ,هœ¨é،¶ç«¯ï¼Œوœ‰
A[PARENT(i)] ≤ A[i] .
هœ¨وœ¬èٹ‚çڑ„ه †وژ’ه؛ڈç®—و³•ن¸ï¼Œوˆ‘ن»¬é‡‡ç”¨çڑ„وک¯وœ€ه¤§ه †ï¼›وœ€ه°ڈه †ï¼Œé€ڑه¸¸هœ¨و„é€ وœ€ه°ڈن¼که…ˆéکںهˆ—و—¶ن½؟用م€‚
ç”±ه‰چé¢ï¼Œهڈ¯çں¥ï¼Œه †هڈ¯ن»¥çœ‹وˆگن¸€و£µو ‘,و‰€ن»¥ï¼Œه †çڑ„é«که؛¦ï¼Œهچ³ن¸؛و ‘çڑ„é«که؛¦ï¼ŒO(lgn)م€‚
و‰€ن»¥ï¼Œن¸€èˆ¬çڑ„و“چن½œï¼Œè؟گè،Œو—¶é—´éƒ½وک¯ن¸؛O(lgn)م€‚
ه…·ن½“,ه¦‚ن¸‹ï¼ڑ
The MAX-HEAPIFYï¼ڑO(lgn) è؟™وک¯ن؟وŒپوœ€ه¤§ه †çڑ„ه…³é”®.
The BUILD-MAX-HEAP:ç؛؟و€§و—¶é—´م€‚هœ¨و— ه؛ڈ输ه…¥و•°ç»„هں؛ç،€ن¸ٹو„é€ وœ€ه¤§ه †م€‚
The HEAPSORTï¼ڑO(nlgn) time, ه †وژ’ه؛ڈç®—و³•وک¯ه¯¹ن¸€ن¸ھو•°ç»„هژںهœ°è؟›è،Œوژ’ه؛ڈ.
The MAX-HEAP-INSERT, HEAP-EXTRACT-MAX, HEAP-INCREASE-KEY, HEAP-MAXIMUMï¼ڑO(lgn)م€‚
هڈ¯ن»¥è®©ه †ن½œن¸؛وœ€ه°ڈن¼که…ˆéکںهˆ—ن½؟用م€‚
ن؟وŒپه †çڑ„و€§è´¨(O(lgn))
ن¸؛ن؛†ن؟وŒپوœ€ه¤§ه †çڑ„و€§è´¨ï¼Œوˆ‘ن»¬è؟گ用MAX-HEAPIFYو“چن½œï¼Œé€’ه½’调用و¤و“چن½œï¼Œن½؟iن¸؛و ¹çڑ„هگو ‘وˆگن¸؛وœ€ه¤§ه †م€‚
MAX-HEAPIFYç®—و³•ï¼Œه¦‚ن¸‹و‰€ç¤؛ï¼ڑ
MAX-HEAPIFY(A, i)
1 l â†گ LEFT(i)
2 r â†گ RIGHT(i)
3 if l ≤ heap-size[A] and A[l] > A[i]
4 then largest â†گ l
5 else largest â†گ i
6 if r ≤ heap-size[A] and A[r] > A[largest]
7 then largest â†گ r
8 if largest ≠i
9 then exchange A[i] <-> A[largest]
10 MAX-HEAPIFY(A, largest)
ه¦‚ن¸ٹ,首ه…ˆç¬¬ن¸€و¥ï¼Œهœ¨ه¯¹ه؛”çڑ„و•°ç»„ه…ƒç´ A[i], ه·¦ه©هگA[LEFT(i)], ه’Œهڈ³ه©هگA[RIGHT(i)]ن¸و‰¾هˆ°وœ€ه¤§çڑ„é‚£ن¸€ن¸ھ,ه°†ه…¶ن¸‹و ‡هکه‚¨هœ¨largestن¸م€‚ه¦‚وœA[i]ه·²ç»ڈه°±وک¯وœ€ه¤§çڑ„ه…ƒç´ ,هˆ™ç¨‹ه؛ڈç›´وژ¥ç»“وںم€‚هگ¦هˆ™ï¼Œiçڑ„وںگن¸ھهگ结点ن¸؛وœ€ه¤§çڑ„ه…ƒç´ ,ه°†ه…¶ï¼Œهچ³A[largest]ن¸ژA[i]ن؛¤وچ¢ï¼Œن»ژ而ن½؟iهڈٹه…¶هگه¥³éƒ½èƒ½و»،足وœ€ه¤§ه †و€§è´¨م€‚ن¸‹و ‡largestو‰€وŒ‡çڑ„ه…ƒç´ هڈکوˆگن؛†A[i]çڑ„ه€¼ï¼Œن¼ڑè؟هڈچوœ€ه¤§ه †و€§è´¨ï¼Œو‰€ن»¥ه¯¹largestو‰€وŒ‡ه…ƒç´ 调用MAX-HEAPIFYم€‚ه¦‚ن¸‹ï¼Œوک¯و¤MAX-HEAPIFYçڑ„و¼”ç¤؛è؟‡ç¨‹ï¼ڑ
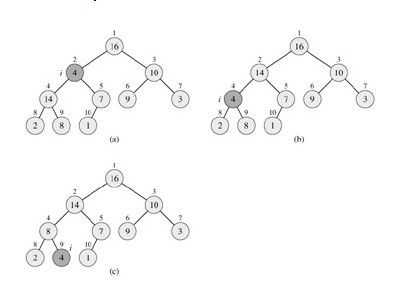
ç”±ن¸ٹه›¾ï¼Œوˆ‘ن»¬ه¾ˆه®¹وک“看ه‡؛,هˆه§‹و„é€ ه‡؛ن¸€وœ€ه¤§ه †ن¹‹هگژ,هœ¨ه…ƒç´ A[i],هچ³16,ه¤§ن؛ژه®ƒçڑ„ن؟©ن¸ھهگ结点4م€پ10,و»،足وœ€ه¤§ه †و€§è´¨م€‚و‰€ن»¥ï¼Œiن¸‹è°ƒوŒ‡هگ‘ç€4,ه°ڈن؛ژ,ه·¦هگ14,و‰€ن»¥ï¼Œè°ƒç”¨MAX-HEAPIFY,4ن¸ژه…¶هگ,14ن؛¤وچ¢ن½چç½®م€‚ن½†4ه¤„هœ¨ن؛†14هژںو¥çڑ„ن½چç½®ن¹‹هگژ,4ه°ڈن؛ژه…¶هڈ³هگ8,هڈˆè؟هڈچن؛†وœ€ه¤§ه †çڑ„و€§è´¨ï¼Œو‰€ن»¥ه†چ递ه½’调用MAX-HEAPIFY,ه°†4ن¸ژ8,ن؛¤وچ¢ن½چç½®م€‚ن؛ژوک¯ï¼Œو»،足ن؛†وœ€ه¤§ه †و€§è´¨ï¼Œç¨‹ه؛ڈ结وںم€‚
MAX-HEAPIFYçڑ„è؟گè،Œو—¶é—´
MAX-HEAPIFYن½œç”¨هœ¨ن¸€و£µن»¥ç»“点iن¸؛و ¹çڑ„م€په¤§ه°ڈن¸؛nçڑ„هگو ‘ن¸ٹو—¶ï¼Œه…¶è؟گè،Œو—¶é—´ن¸؛è°ƒو•´ه…ƒç´ A[i]م€پA[LEFT(i)],A[RIGHT(i)]çڑ„ه…³ç³»و—¶و‰€ç”¨و—¶é—´ن¸؛O(1),ه†چهٹ ن¸ٹ,ه¯¹ن»¥içڑ„وںگن¸ھهگ结点ن¸؛و ¹çڑ„هگو ‘调用MAX-HEAPIFYو‰€éœ€çڑ„و—¶é—´ï¼Œن¸”i结点çڑ„هگو ‘ه¤§ه°ڈ至ه¤ڑن¸؛2n/3,و‰€ن»¥ï¼ŒMAX-HEAPIFYçڑ„è؟گè،Œو—¶é—´ن¸؛
T (n) ≤ T(2n/3) + خک(1).
وˆ‘ن»¬ï¼Œهڈ¯ن»¥è¯په¾—و¤ه¼ڈهگçڑ„递ه½’解ن¸؛T(n)=O(lgn)م€‚ه…·ن½“è¯پو³•ï¼Œهڈ¯هڈ‚考算و³•ه¯¼è®؛第6ç« ن¹‹6.2èٹ‚,è؟™é‡Œï¼Œç•¥è؟‡م€‚
ه»؛ه †(O(N))
BUILD-MAX-HEAP(A)
1 heap-size[A] â†گ length[A]
2 for i â†گ |_length[A]/2_| downto 1
3 do MAX-HEAPIFY(A, i) //ه»؛ه †ï¼Œو€ژن¹ˆه»؛هˆ—?هژںو¥ه°±وک¯ن¸چو–çڑ„调用MAX-HEAPIFY(A, i)و¥ه»؛ç«‹وœ€ه¤§ه †م€‚
BUILD-MAX-HEAPé€ڑè؟‡ه¯¹و¯ڈن¸€ن¸ھه…¶ه®ƒç»“点,都调用ن¸€و¬،MAX-HEAPIFY,
و¥ه»؛ç«‹ن¸€ن¸ھن¸ژو•°ç»„A[1...n]相ه¯¹ه؛”çڑ„وœ€ه¤§ه †م€‚A[(|_n/2_|+1) ‥ n]ن¸çڑ„ه…ƒç´ 都وک¯و ‘ن¸çڑ„هڈ¶هگم€‚
ه› و¤ï¼Œè‡ھ然而然,و¯ڈن¸ھ结点,都هڈ¯ن»¥çœ‹ن½œن¸€ن¸ھهڈھهگ«ن¸€ن¸ھه…ƒç´ çڑ„ه †م€‚
ه…³ن؛ژو¤è؟‡ç¨‹BUILD-MAX-HEAP(A)çڑ„و£ç،®و€§ï¼Œهڈ¯هڈ‚考算و³•ه¯¼è®؛ 第6ç« ن¹‹6.3èٹ‚م€‚
ن¸‹ه›¾ï¼Œوک¯ن¸€ن¸ھو¤è؟‡ç¨‹çڑ„ن¾‹هگï¼ڑ
BUILD-MAX-HEAPçڑ„è؟گè،Œو—¶é—´
ه› ن¸؛و¯ڈو¬،调用MAX-HEAPPIFYçڑ„و—¶é—´ن¸؛O(lgn),而ه…±وœ‰O(n)و¬،调用,و‰€ن»¥BUILD-MAX-HEAPçڑ„简هچ•ن¸ٹç•Œن¸؛O(nlgn)م€‚ç®—و³•ه¯¼è®؛ن¸€ن¹¦وڈگهˆ°ï¼Œه°½ç®،è؟™ن¸ھو—¶é—´ç•Œوک¯ه¯¹çڑ„,ن½†ن»ژو¸گè؟›و„ڈن¹‰ن¸ٹ,è؟کن¸چه¤ںç²¾ç،®م€‚
é‚£ن¹ˆï¼Œو›´ç²¾ç،®çڑ„و—¶é—´ç•Œï¼Œوک¯ه¤ڑه°‘هˆ—?
ç”±ن؛ژ,MAX-HEAPIFYهœ¨و ‘ن¸ن¸چهگŒé«که؛¦çڑ„结点ه¤„è؟گè،Œçڑ„و—¶é—´ن¸چهگŒï¼Œن¸”ه¤§éƒ¨هˆ†ç»“点çڑ„é«که؛¦éƒ½و¯”较ه°ڈ,
而وˆ‘ن»¬çں¥éپ“,ن¸€nن¸ھه…ƒç´ çڑ„ه †çڑ„é«که؛¦ن¸؛|_lgn_|(هگ‘ن¸‹هڈ–و•´),ن¸”هœ¨ن»»و„ڈé«که؛¦hن¸ٹ,至ه¤ڑوœ‰|-n/2^h+1-|(هگ‘ن¸ٹهڈ–و•´)ن¸ھ结点م€‚
ه› و¤ï¼ŒMAX-HEAPIFYن½œç”¨هœ¨é«که؛¦ن¸؛hçڑ„结点ن¸ٹçڑ„و—¶é—´ن¸؛O(h),و‰€ن»¥ï¼ŒBUILD-MAX-HEAPçڑ„ن¸ٹç•Œن¸؛ï¼ڑO(n)م€‚ه…·ن½“وژ¨ه¯¼è؟‡ç¨‹ï¼Œç•¥م€‚
ن¸‰م€په †وژ’ه؛ڈç®—و³•
و‰€è°“çڑ„ه †وژ’ه؛ڈ,ه°±وک¯è°ƒç”¨ن¸ٹè؟°ن؟©ن¸ھè؟‡ç¨‹ï¼ڑن¸€ن¸ھه»؛ه †çڑ„و“چن½œم€پBUILD-MAX-HEAP,ن¸€ن¸ھن؟وŒپوœ€ه¤§ه †çڑ„و“چن½œم€پMAX-HEAPIFYم€‚详细算و³•ه¦‚ن¸‹ï¼ڑ
HEAPSORT(A) //n-1و¬،调用MAX-HEAPIFY,و‰€ن»¥ï¼ŒO(n*lgn)
1 BUILD-MAX-HEAP(A) //ه»؛وœ€ه¤§ه †ï¼ŒO(n)
2 for i â†گ length[A] downto 2
3 do exchange A[1] <-> A[i]
4 heap-size[A] â†گ heap-size[A] - 1
5 MAX-HEAPIFY(A, 1) //ن؟وŒپه †çڑ„و€§è´¨ï¼ŒO(lgn)
ه¦‚ن¸ٹ,هچ³وک¯ه †وژ’ه؛ڈç®—و³•çڑ„ه®Œو•´è،¨è؟°م€‚ن¸‹é¢ï¼Œه†چè´´ن¸€ن¸‹ن¸ٹè؟°ه †وژ’ه؛ڈç®—و³•ن¸çڑ„ن؟©ن¸ھه»؛ه †م€پن¸ژن؟وŒپوœ€ه¤§ه †و“چن½œï¼ڑ
BUILD-MAX-HEAP(A) //ه»؛ه †
1 heap-size[A] â†گ length[A]
2 for i â†گ |_length[A]/2_| downto 1
3 do MAX-HEAPIFY(A, i)
MAX-HEAPIFY(A, i)//ن؟وŒپوœ€ه¤§ه †
1 l â†گ LEFT(i)
2 r â†گ RIGHT(i)
3 if l ≤ heap-size[A] and A[l] > A[i]
4 then largest â†گ l
5 else largest â†گ i
6 if r ≤ heap-size[A] and A[r] > A[largest]
7 then largest â†گ r
8 if largest ≠i
9 then exchange A[i] <-> A[largest]
10 MAX-HEAPIFY(A, largest)
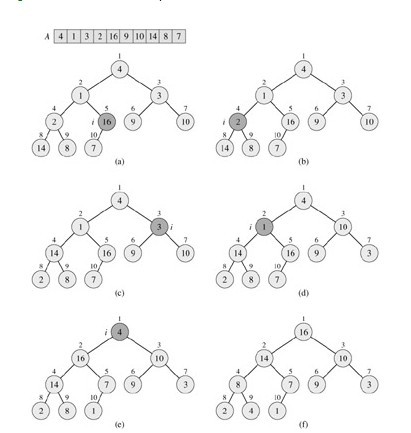
ن»¥ن¸‹وک¯ï¼Œه †وژ’ه؛ڈç®—و³•çڑ„و¼”ç¤؛è؟‡ç¨‹ï¼ˆé€ڑè؟‡ï¼Œé،¶ç«¯وœ€ه¤§çڑ„ه…ƒç´ ن¸ژوœ€هگژن¸€ن¸ھه…ƒç´ ن¸چو–çڑ„ن؛¤وچ¢ï¼Œن؛¤وچ¢هگژهڈˆن¸چو–çڑ„调用MAX-HEAPIFYن»¥é‡چو–°ç»´وŒپوœ€ه¤§ه †çڑ„و€§è´¨ï¼Œوœ€هگژ,ن¸€ن¸ھن¸€ن¸ھçڑ„,ن»ژه¤§هˆ°ه°ڈçڑ„,وٹٹه †ن¸çڑ„و‰€وœ‰ه…ƒç´ 都و¸…çگ†وژ‰ï¼Œن¹ںه°±ه½¢وˆگن؛†ن¸€ن¸ھوœ‰ه؛ڈçڑ„ه؛ڈهˆ—م€‚è؟™ه°±وک¯ه †وژ’ه؛ڈçڑ„ه…¨éƒ¨è؟‡ç¨‹م€‚)ï¼ڑ

ن¸ٹه›¾ن¸ï¼Œa->b,b->c,....ن¹‹é—´ï¼Œéƒ½وœ‰ن¸€ن¸ھé،¶ç«¯وœ€ه¤§ه…ƒç´ ن¸ژوœ€ه°ڈه…ƒç´ ن؛¤وچ¢هگژ,调用MAX-HEAPIFYçڑ„è؟‡ç¨‹ï¼Œوˆ‘ن»¬çں¥éپ“,و¤MAX-HEAPIFYçڑ„è؟گè،Œو—¶é—´ن¸؛O(lgn),而è¦په®Œوˆگو•´ن¸ھه †وژ’ه؛ڈçڑ„è؟‡ç¨‹ï¼Œه…±è¦پç»ڈè؟‡O(n)و¬،è؟™و ·çڑ„MAX-HEAPIFYو“چن½œم€‚و‰€ن»¥ï¼Œو‰چوœ‰ه †وژ’ه؛ڈç®—و³•çڑ„è؟گè،Œو—¶é—´ن¸؛O(n*lgn)م€‚
ه®Œم€‚
وœ¬ن؛؛Julyه¯¹وœ¬هچڑه®¢و‰€وœ‰ن»»ن½•و–‡ç« م€په†…ه®¹ه’Œèµ„و–™ن؛«وœ‰ç‰ˆوƒم€‚
转载هٹ،ه؟…و³¨وکژن½œè€…وœ¬ن؛؛هڈٹه‡؛ه¤„,ه¹¶é€ڑçں¥وœ¬ن؛؛م€‚ن؛Œé›¶ن¸€ن¸€ه¹´ن؛Œوœˆن؛Œهچپن¸€و—¥م€‚
هˆ†ن؛«هˆ°ï¼ڑ














相ه…³وژ¨èچگ
هœ¨م€ٹç²¾é€ڑه…«ه¤§وژ’ه؛ڈç®—و³•ç³»هˆ—ï¼ڑن¸€م€په؟«é€ںوژ’ه؛ڈç®—و³•م€‹ن¸ï¼Œو–‡ç« 详细解é‡ٹن؛†ه؟«é€ںوژ’ه؛ڈçڑ„è؟‡ç¨‹ï¼ŒهŒ…و‹¬ه¦‚ن½•é€‰و‹©هں؛ه‡†ه…ƒç´ ,ن»¥هڈٹه¦‚ن½•è؟›è،Œهˆ†هŒ؛و“چن½œم€‚هگŒو—¶ï¼Œوڈگن¾›ن؛†ن¼ھن»£ç په’Œه®çژ°ن»£ç پ,ه¸®هٹ©è¯»è€…و›´ه¥½هœ°çگ†è§£ه’Œه؛”用ه؟«é€ںوژ’ه؛ڈم€‚ 2. **ه†’و³،...
- **وژ’ه؛ڈç®—و³•**ï¼ڑهŒ…و‹¬ه†’و³،وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈم€په †وژ’ه؛ڈç‰ï¼Œه®ƒن»¬وک¯و•°وچ®ه¤„çگ†çڑ„هں؛ç،€ï¼Œçگ†è§£ه’ŒوژŒوڈ،هگ„ç§چوژ’ه؛ڈç®—و³•çڑ„و—¶é—´ه¤چو‚ه؛¦ه’Œç©؛é—´ه¤چو‚ه؛¦ه¯¹ن¼کهŒ–程ه؛ڈو€§èƒ½è‡³ه…³é‡چè¦پم€‚ - **وں¥و‰¾ç®—و³•**ï¼ڑه¦‚ç؛؟و€§...
1. **وژ’ه؛ڈç®—و³•**ï¼ڑن¹¦ن¸هڈ¯èƒ½هŒ…و‹¬ن؛†ه†’و³،وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈم€په †وژ’ه؛ڈç‰ç»ڈه…¸çڑ„وژ’ه؛ڈç®—و³•ï¼Œè؟™ن؛›ç®—و³•هœ¨ه®é™…ه؛”用ن¸ه¹؟و³›ن½؟用,وک¯و¯ڈن¸€ن½چ程ه؛ڈه‘که؟…ه¤‡çڑ„هں؛ç،€çں¥è¯†م€‚و؛گç پن¸ï¼Œن½ هڈ¯ن»¥çœ‹هˆ°و¯ڈç§چوژ’ه؛ڈç®—و³•هœ¨Cم€پ...
1. **وژ’ه؛ڈç®—و³•**ï¼ڑه†’و³،وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈم€په †وژ’ه؛ڈç‰م€‚ن؛†è§£ه®ƒن»¬çڑ„هژںçگ†م€پو€§èƒ½هˆ†وگن»¥هڈٹ适用هœ؛و™¯ه¯¹ن؛ژن¼کهŒ–ن»£ç پ至ه…³é‡چè¦پم€‚ 2. **وں¥و‰¾ç®—و³•**ï¼ڑé،؛ه؛ڈوں¥و‰¾م€پن؛Œهˆ†وں¥و‰¾م€په“ˆه¸Œوں¥و‰¾ç‰م€‚ن؛Œهˆ†وں¥و‰¾هœ¨وœ‰ه؛ڈ...
1. **وژ’ه؛ڈç®—و³•**ï¼ڑهŒ…و‹¬ه؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈم€په †وژ’ه؛ڈم€په†’و³،وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈç‰م€‚ه؟«é€ںوژ’ه؛ڈن»¥ه…¶ه¹³ه‡و—¶é—´ه¤چو‚ه؛¦ن¸؛O(n log n)而著هگچ,ه½’ه¹¶وژ’ه؛ڈهˆ™ه› ه…¶ç¨³ه®ڑو€§è€Œهڈ—é’çگم€‚ه †وژ’ه؛ڈهˆ©ç”¨ن؛†ه †و•°وچ®ç»“و„çڑ„特و€§ï¼Œè€Œه†’و³،ه’Œوڈ’ه…¥وژ’ه؛ڈهˆ™é€‚用...
1. **وژ’ه؛ڈç®—و³•**ï¼ڑوژ’ه؛ڈوک¯هں؛ç،€ن¸çڑ„هں؛ç،€ï¼Œه¦‚ه†’و³،وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈه’Œه †وژ’ه؛ڈç‰م€‚و¯ڈç§چوژ’ه؛ڈç®—و³•éƒ½وœ‰ه…¶ç‰¹ه®ڑçڑ„ه؛”用هœ؛و™¯ه’Œو•ˆçژ‡ç‰¹ç‚¹ï¼Œçگ†è§£è؟™ن؛›ç®—و³•وœ‰هٹ©ن؛ژوˆ‘ن»¬هœ¨é¢ه¯¹ن¸چهگŒو•°وچ®é›†و—¶هپڑه‡؛وœ€ن¼ک选و‹©م€‚ 2...
1. **وژ’ه؛ڈç®—و³•**ï¼ڑه¦‚ه†’و³،وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈه’Œه †وژ’ه؛ڈç‰م€‚è؟™ن؛›وژ’ه؛ڈç®—و³•çڑ„ن¸چهگŒن¹‹ه¤„هœ¨ن؛ژه®ƒن»¬çڑ„و•ˆçژ‡م€پ稳ه®ڑو€§ن»¥هڈٹه¦‚ن½•ن؛¤وچ¢ه’Œو¯”较ه…ƒç´ م€‚ 2. **وں¥و‰¾ç®—و³•**ï¼ڑهŒ…و‹¬ç؛؟و€§وں¥و‰¾م€پن؛Œهˆ†وں¥و‰¾ه’Œه“ˆه¸Œوں¥و‰¾م€‚...
1. وژ’ه؛ڈç®—و³•ï¼ڑهŒ…و‹¬ه†’و³،وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈم€په †وژ’ه؛ڈç‰م€‚Javaçڑ„Collectionsو،†و¶وڈگن¾›ن؛†sortو–¹و³•ï¼Œه†…部ن½؟用ن؛†é«کو•ˆçڑ„TimSortç®—و³•م€‚ 2. وگœç´¢ç®—و³•ï¼ڑç؛؟و€§وگœç´¢م€پن؛Œهˆ†وگœç´¢ï¼ˆé€‚用ن؛ژوœ‰ه؛ڈو•°ç»„وˆ–وگœç´¢و ‘...
- وژ’ه؛ڈç®—و³•ï¼ڑه†’و³،وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈه’Œه †وژ’ه؛ڈ - ه†’و³،ه’Œé€‰و‹©وژ’ه؛ڈï¼ڑ简هچ•ن½†و•ˆçژ‡è¾ƒن½ژ - وڈ’ه…¥ه’Œه؟«é€ںوژ’ه؛ڈï¼ڑه¹³ه‡وƒ…ه†µن¸‹و•ˆçژ‡è¾ƒé«ک - ه½’ه¹¶ه’Œه †وژ’ه؛ڈï¼ڑوœ€هڈوƒ…ه†µن¸‹ن»چن؟وŒپ稳ه®ڑو•ˆçژ‡ - وگœç´¢ç®—و³•ï¼ڑ...
1. وژ’ه؛ڈç®—و³•ï¼ڑC#ن¸ه®çژ°وژ’ه؛ڈçڑ„ه…¸ه‹ç®—و³•وœ‰ه†’و³،وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈم€په †وژ’ه؛ڈç‰م€‚ن¾‹ه¦‚,Arrayç±»وڈگن¾›Sort()و–¹و³•ï¼Œهڈ¯ن»¥ه¯¹و•°ç»„è؟›è،Œه؟«é€ںوژ’ه؛ڈم€‚ 2. وگœç´¢ç®—و³•ï¼ڑç؛؟و€§وگœç´¢م€پن؛Œهˆ†وگœç´¢م€په“ˆه¸Œوگœç´¢ç‰م€‚C#çڑ„...
10. **وژ’ه؛ڈç®—و³•**ï¼ڑه†’و³،وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈم€په †وژ’ه؛ڈم€پè®،و•°وژ’ه؛ڈم€پو،¶وژ’ه؛ڈه’Œهں؛و•°وژ’ه؛ڈç‰éƒ½وک¯ه¸¸è§پçڑ„وژ’ه؛ڈç®—و³•ï¼Œه®ƒن»¬هœ¨ن¸چهگŒهœ؛و™¯ن¸‹وœ‰ن¸چهگŒçڑ„و€§èƒ½è،¨çژ°م€‚ 11. **وں¥و‰¾ç®—و³•**ï¼ڑé،؛ه؛ڈوں¥و‰¾م€پن؛Œهˆ†وں¥و‰¾م€پ...
3. **وژ’ه؛ڈه’Œوگœç´¢ç®—و³•**ï¼ڑهŒ…و‹¬ه†’و³،وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈم€پن؛Œهˆ†وں¥و‰¾م€په“ˆه¸Œوں¥و‰¾ç‰م€‚è؟™ن؛›ç®—و³•هœ¨ه¤„çگ†ه¤§é‡ڈو•°وچ®و—¶èµ·ç€ه…³é”®ن½œç”¨م€‚ 4. **ه›¾è®؛ç®—و³•**ï¼ڑه¦‚و·±ه؛¦ن¼که…ˆوگœç´¢ï¼ˆDFS)م€په¹؟ه؛¦ن¼که…ˆوگœç´¢ï¼ˆBFS)م€پ...
1. **وژ’ه؛ڈç®—و³•**ï¼ڑPythonن¸ه¸¸è§پçڑ„وژ’ه؛ڈç®—و³•وœ‰ه†’و³،وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈç‰م€‚ن؛†è§£ه®ƒن»¬çڑ„هں؛وœ¬هژںçگ†ه’Œو—¶é—´ه¤چو‚ه؛¦ه¯¹ن؛ژن¼کهŒ–ن»£ç پو€§èƒ½è‡³ه…³é‡چè¦پم€‚ 2. **ن؛Œهˆ†وں¥و‰¾**ï¼ڑن؛Œهˆ†وں¥و‰¾وک¯ن¸€ç§چهœ¨وœ‰ه؛ڈو•°ç»„ن¸وں¥و‰¾...
وژ’ه؛ڈç®—و³•ه¦‚ه†’و³،وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈه’Œه †وژ’ه؛ڈ,هگ„وœ‰ه…¶ç‰¹ç‚¹ه’Œé€‚用هœ؛و™¯ï¼Œçگ†è§£ه®ƒن»¬çڑ„ه·¥ن½œهژںçگ†وœ‰هٹ©ن؛ژهœ¨ه®é™…编程ن¸é€‰و‹©وœ€هگˆé€‚çڑ„ç®—و³•م€‚ وگœç´¢ç®—و³•و–¹é¢ï¼Œن¹¦ن¸è¯¦ç»†è®²è§£ن؛†ç؛؟و€§وگœç´¢م€پن؛Œهˆ†وگœç´¢ن»¥هڈٹه“ˆه¸Œ...
1. وژ’ه؛ڈç®—و³•ï¼ڑهŒ…و‹¬ه†’و³،وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈم€په †وژ’ه؛ڈç‰ï¼Œه®ƒن»¬ç”¨ن؛ژه°†و•°وچ®وŒ‰ç…§ç‰¹ه®ڑé،؛ه؛ڈوژ’هˆ—م€‚ 2. وگœç´¢ç®—و³•ï¼ڑه¦‚ç؛؟و€§وگœç´¢م€پن؛Œهˆ†وگœç´¢م€په“ˆه¸Œè،¨وگœç´¢ï¼Œه¸®هٹ©هœ¨و•°وچ®é›†ن¸و‰¾هˆ°ç‰¹ه®ڑه…ƒç´ م€‚ 3. ه›¾ه½¢ç®—و³•ï¼ڑ...
8. **وژ’ه؛ڈç®—و³•**ï¼ڑ除ن؛†ه‰چé¢وڈگهˆ°çڑ„وژ’ه؛ڈç®—و³•ï¼Œè؟کوœ‰ه½’ه¹¶وژ’ه؛ڈم€په¸Œه°”وژ’ه؛ڈم€په †وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈçڑ„هڈکن½“ç‰م€‚é—®é¢کهڈ¯èƒ½è¦پو±‚هˆ†وگن¸چهگŒوژ’ه؛ڈç®—و³•çڑ„و—¶é—´ه¤چو‚ه؛¦ه’Œç¨³ه®ڑو€§م€‚ 9. **وں¥و‰¾ç®—و³•**ï¼ڑن؛Œهˆ†وں¥و‰¾م€پن؛Œهڈ‰وگœç´¢و ‘وں¥و‰¾م€په“ˆه¸Œوں¥و‰¾ç‰ï¼Œ...
2.1 وژ’ه؛ڈç®—و³•ï¼ڑهŒ…و‹¬ه؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈم€په †وژ’ه؛ڈç‰م€‚C++و ‡ه‡†ه؛“ن¸çڑ„`std::sort`هڈ¯ن»¥è؟›è،Œç®€هچ•é«کو•ˆçڑ„وژ’ه؛ڈم€‚ 2.2 وں¥و‰¾ç®—و³•ï¼ڑç؛؟و€§وں¥و‰¾م€پن؛Œهˆ†وں¥و‰¾ç‰م€‚ن؛Œهˆ†وں¥و‰¾é€‚用ن؛ژه·²وژ’ه؛ڈçڑ„و•°ç»„,و•ˆçژ‡è¾ƒé«کم€‚ 2.3 هˆ†و²»ç–ç•¥ï¼ڑه°†ه¤§é—®é¢کهˆ†è§£ن¸؛...
1. **وژ’ه؛ڈç®—و³•**ï¼ڑهŒ…و‹¬ه؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€په†’و³،وژ’ه؛ڈç‰ï¼Œه®ƒن»¬وک¯è§£ه†³و•°وچ®ç»„织问é¢کçڑ„هں؛ç،€م€‚ه؟«é€ںوژ’ه؛ڈن»¥ه…¶ه¹³ه‡و—¶é—´ه¤چو‚ه؛¦O(n log n)而著هگچ,而وڈ’ه…¥وژ’ه؛ڈه’Œه†’و³،وژ’ه؛ڈهˆ™é€‚用ن؛ژه°ڈ规و¨،وˆ–部هˆ†وœ‰ه؛ڈçڑ„و•°وچ®م€‚ ...
2. **وژ’ه؛ڈن¸ژوگœç´¢ç®—و³•**ï¼ڑهŒ…و‹¬ه†’و³،وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈم€په †وژ’ه؛ڈç‰ç»ڈه…¸وژ’ه؛ڈç®—و³•ï¼Œن»¥هڈٹç؛؟و€§وگœç´¢م€پن؛Œهˆ†وگœç´¢م€په“ˆه¸Œوں¥و‰¾ç‰وگœç´¢ç®—و³•م€‚è؟™ن؛›ç®—و³•ن¸چن»…需è¦پçگ†è§£ه…¶ه·¥ن½œهژںçگ†ï¼Œè؟ک需è¦پوژŒوڈ،ه…¶و—¶é—´ه¤چو‚ه؛¦ه’Œ...
5. **وژ’ه؛ڈن¸ژوں¥و‰¾**ï¼ڑوژ’ه؛ڈç®—و³•وœ‰ه†’و³،وژ’ه؛ڈم€پ选و‹©وژ’ه؛ڈم€پوڈ’ه…¥وژ’ه؛ڈم€په؟«é€ںوژ’ه؛ڈم€په½’ه¹¶وژ’ه؛ڈç‰ï¼›وں¥و‰¾ç®—و³•وœ‰é،؛ه؛ڈوں¥و‰¾م€پن؛Œهˆ†وں¥و‰¾م€په“ˆه¸Œوں¥و‰¾ç‰م€‚وژ’ه؛ڈه’Œوں¥و‰¾ç®—و³•çڑ„و•ˆçژ‡ç›´وژ¥ه½±ه“چ程ه؛ڈو€§èƒ½م€‚ 6. **هٹ¨و€پ规هˆ’**ï¼ڑه¸¸ç”¨ن؛ژ解ه†³وœ€ن¼کهŒ–é—®é¢ک...