一之续、A*，Dijkstra，BFS算法性能比较及A*算法的应用

一之续、A*，Dijkstra，双向BFS算法性能比较及A*算法的应用

作者:July 二零一一年三月十日。
出处：http://blog.csdn.net/v_JULY_v
--------------------------------------------------

 

引言：
最短路径的各路算法A*算法、Dijkstra 算法、BFS算法，都已在本BLOG内有所阐述了。其中，Dijkstra 算法，后又写了一篇文章继续阐述：二（续）、理解Dijkstra算法。但，想必，还是有部分读者对此类最短路径算法，并非已了然于胸，或者，无一个总体大概的印象。

本文，即以演示图的形式，比较它们各自的寻路过程，让各位对它们有一个清晰而直观的印象。
我们比较，以下五种算法：
1. A* (使用曼哈顿距离)
2. A* (采用欧氏距离)
3. A* (利用切比雪夫距离)
4. Dijkstra
5. Bi-Directional Breadth-First-Search(双向广度优先搜索)

咱们以下图为例，图上绿色方块代表起始点，红色方块代表目标点，紫色的方块代表障碍物，白色的方块代表可以通行的路径。
下面，咱们随意摆放起始点绿块，目标点红块的位置，然后，在它们中间随便画一些障碍物，
最后，运行程序，比较使用上述五种算法，得到各自不同的路径，各自找寻过程中所覆盖的范围，各自的工作流程，并从中可以窥见它们的效率高低。

A*、Dijkstra、BFS算法性能比较演示：
ok，任意摆放绿块与红块的三种状态：
一、起始点绿块，与目标点红块在同一条水平线上：

各自的搜寻路径为：
1. A* (使用曼哈顿距离)

2. A* (采用欧氏距离)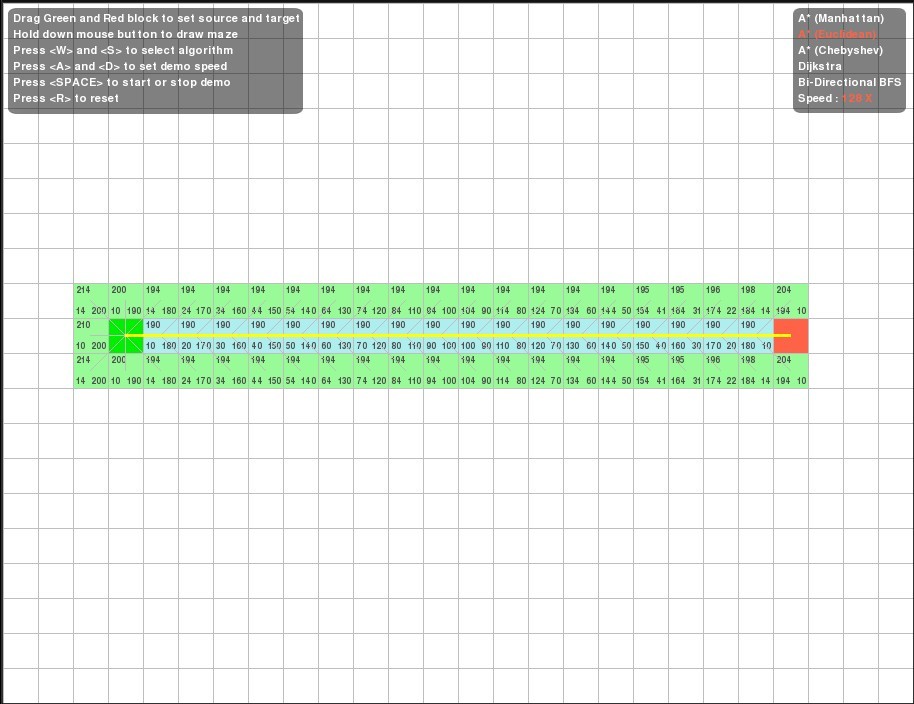

3. A* (利用切比雪夫距离)

4. Dijkstra 算法.//很明显，Dijkstra 搜寻效率明显差于上述A*算法。（看它最后找到目标点红块所走过的路径，和覆盖的范围，即能轻易看出来，下面的比较，也是基于同一个道理。看路径，看覆盖的范围，评价一个算法的效率）。

5. Bi-Directional Breadth-First-Search(双向广度优先搜索)

 

二、起始点绿块，目标点红块在一斜线上：

各自的搜寻路径为：
1. A* (使用曼哈顿距离)

2. A* (采用欧氏距离)

3. A* (利用切比雪夫距离)

4. Dijkstra 算法。 //与上述A* 算法比较，覆盖范围大，搜寻效率较低。

5. Bi-Directional Breadth-First-Search(双向广度优先搜索)

 

三、起始点绿块，目标点红块被多重障碍物阻挡：

各自的搜寻路径为（同样，还是从绿块到红块）：
1. A* (使用曼哈顿距离)

2. A* (采用欧氏距离)..

3. A* (利用切比雪夫距离)

4. Dijkstra....

5. Bi-Directional Breadth-First-Search(双向广度优先搜索) //覆盖范围同上述Dijkstra 算法一样很大，效率低下。

A*搜寻算法的高效之处
如上，是不是对A*、Dijkstra、双向BFS算法各自的性能有了个总体大概的印象列?由上述演示，我们可以看出，在最短路径搜寻效率上，一般有A*>Dijkstra、双向BFS，其中Dijkstra、双向BFS到底哪个算法更优，还得看具体情况。
由上，我们也可以看出，A*搜寻算法的确是一种比较高效的寻路算法。

A*算法最为核心的过程，就在每次选择下一个当前搜索点时，是从所有已探知的但未搜索过点中(可能是不同层，亦可不在同一条支路上)，选取f值最小的结点进行展开。
而所有“已探知的但未搜索过点”可以通过一个按f值升序的队列(即优先队列)进行排列。
这样，在整体的搜索过程中，只要按照类似广度优先的算法框架，从优先队列中弹出队首元素（f值），对其可能子结点计算g、h和f值，直到优先队列为空(无解)或找到终止点为止。

A*算法与广度、深度优先和Dijkstra 算法的联系就在于：当g(n)=0时，该算法类似于DFS，当h(n)=0时，该算法类似于BFS。且同时，如果h(n)为0，只需求出g(n)，即求出起点到任意顶点n的最短路径，则转化为单源最短路径问题，即Dijkstra算法。这一点，可以通过上面的A*搜索树的具体过程中将h(n)设为0或将g(n)设为0而得到。

BFS、DFS、Kruskal、Prim、Dijkstra算法时间复杂度
上面，既然提到了A*算法与广度、深度优先搜索算法的联系，那么，下面，也顺便再比较下BFS、DFS、Kruskal、Prim、Dijkstra算法时间复杂度吧：
一般说来，我们知道，BFS，DFS算法的时间复杂度为O（V+E），
最小生成树算法Kruskal、Prim算法的时间复杂度为O（E*lgV）。
而Prim算法若采用斐波那契堆实现的话，算法时间复杂度为O（E+V*lgV），当|V|<<|E|时，E+V*lgV是一个较大的改进。
//|V|<<|E|，=>O（E+V*lgV） << O（E*lgV），对吧。:D
Dijkstra 算法，斐波纳契堆用作优先队列时，算法时间复杂度为O（V*lgV + E）。
//看到了吧，与Prim算法采用斐波那契堆实现时，的算法时间复杂度是一样的。

所以我们，说，BFS、Prime、Dijkstra 算法是有相似之处的，单从各算法的时间复杂度比较看，就可窥之一二。

A*搜寻算法的思想
ok，既然，A*搜寻算法作为是一种好的、高效的寻路算法，咱们就来想办法实现它吧。
实现一个算法，首先得明确它的算法思想，以及算法的步骤与流程，从我之前的一篇文章中，可以了解到：
A*算法，作为启发式算法中很重要的一种，被广泛应用在最优路径求解和一些策略设计的问题中。
而A*算法最为核心的部分，就在于它的一个估值函数的设计上：

f(n)=g(n)+h(n)

其中f(n)是每个可能试探点的估值，它有两部分组成：
一部分，为g(n)，它表示从起始搜索点到当前点的代价（通常用某结点在搜索树中的深度来表示）。
另一部分，即h(n)，它表示启发式搜索中最为重要的一部分，即当前结点到目标结点的估值，

h(n)设计的好坏，直接影响着具有此种启发式函数的启发式算法的是否能称为A*算法。

一种具有f(n)=g(n)+h(n)策略的启发式算法能成为A*算法的充分条件是：

1、搜索树上存在着从起始点到终了点的最优路径。
2、问题域是有限的。
3、所有结点的子结点的搜索代价值>0。
4、h(n)=<h*(n) （h*(n)为实际问题的代价值）。

当此四个条件都满足时，一个具有f(n)=g(n)+h(n)策略的启发式算法能成为A*算法，并一定能找到最优解。
对于一个搜索问题，显然，条件1,2,3都是很容易满足的，而条件4： h(n)<=h*(n)是需要精心设计的，由于h*(n)显然是无法知道的，所以，一个满足条件4的启发策略h(n)就来的难能可贵了。

不过，对于图的最优路径搜索和八数码问题，有些相关策略h(n)不仅很好理解，而且已经在理论上证明是满足条件4的，从而为这个算法的推广起到了决定性的作用。

A*搜寻算法的应用
ok，咱们就来应用A*搜寻算法实现八数码问题，下面，就是其主体代码，由于给的注释很详尽，就不再啰嗦了，有任何问题，请不吝指正：

//节点结构体
typedef struct Node
{
int data[9];
double f,g;
struct Node * parent;
}Node,*Lnode;

//OPEN CLOSED 表结构体
typedef struct Stack
{
Node * npoint;
struct Stack * next;
}Stack,* Lstack;

//选取OPEN表上f值最小的节点，返回该节点地址
Node * Minf(Lstack * Open)
{
Lstack temp = (*Open)->next,min = (*Open)->next,minp = (*Open);
Node * minx;
while(temp->next != NULL)
{
if((temp->next ->npoint->f) < (min->npoint->f))
{
min = temp->next;
minp = temp;
}
temp = temp->next;
}
minx = min->npoint;
temp = minp->next;
minp->next = minp->next->next;
free(temp);
return minx;
}

//判断是否可解
int Canslove(Node * suc, Node * goal)
{
int a = 0,b = 0,i,j;
for(i = 1; i< 9;i++)
for(j = 0;j < i;j++)
{
if((suc->data[i] > suc->data[j]) && suc->data[j] != 0)
a++;
if((goal->data[i] > goal->data[j]) && goal->data[j] != 0)
b++;
}
if(a%2 == b%2)
return 1;
else
return 0;
}

//判断节点是否相等 ，1相等，0不相等
int Equal(Node * suc,Node * goal)
{
for(int i = 0; i < 9; i ++ )
if(suc->data[i] != goal->data[i])return 0;
return 1;
}

//判断节点是否属于OPEN表 或 CLOSED表，是则返回节点地址，否则返回空地址
Node * Belong(Node * suc,Lstack * list)
{
Lstack temp = (*list) -> next ;
if(temp == NULL)return NULL;
while(temp != NULL)
{
if(Equal(suc,temp->npoint))return temp -> npoint;
temp = temp->next;
}
return NULL;
}

//把节点放入OPEN 或CLOSED 表中
void Putinto(Node * suc,Lstack * list)
{
Stack * temp;
temp =(Stack *) malloc(sizeof(Stack));
temp->npoint = suc;
temp->next = (*list)->next;
(*list)->next = temp;
}

///////////////计算f值部分-开始//////////////////////////////
double Fvalue(Node suc, Node goal, float speed)
{//计算f值
double Distance(Node,Node,int);
double h = 0;
for(int i = 1; i <= 8; i++)
h = h + Distance(suc, goal, i);
return h*speed + suc.g; //f = h + g（speed值增加时搜索过程以找到目标为优先因此可能不会返

回最优解）
}
double Distance(Node suc, Node goal, int i)
{//计算方格的错位距离
int k,h1,h2;
for(k = 0; k < 9; k++)
{
if(suc.data[k] == i)h1 = k;
if(goal.data[k] == i)h2 = k;
}
return double(fabs(h1/3 - h2/3) + fabs(h1%3 - h2%3));
}
///////////////计算f值部分-结束//////////////////////////////

 

///////////////////////扩展后继节点部分的函数-开始/////////////////
int BelongProgram(Lnode * suc ,Lstack * Open ,Lstack * Closed ,Node goal ,float speed)
{//判断子节点是否属于OPEN或CLOSED表 并作出相应的处理
Node * temp = NULL;
int flag = 0;
if((Belong(*suc,Open) != NULL) || (Belong(*suc,Closed) != NULL))
{
if(Belong(*suc,Open) != NULL) temp = Belong(*suc,Open);
else temp = Belong(*suc,Closed);
if(((*suc)->g) < (temp->g))
{
temp->parent = (*suc)->parent;
temp->g = (*suc)->g;
temp->f = (*suc)->f;
flag = 1;
}
}
else
{
Putinto(* suc, Open);
(*suc)->f = Fvalue(**suc, goal, speed);
}
return flag;
}

void Spread(Lnode * suc, Lstack * Open, Lstack * Closed, Node goal, float speed)
{//扩展后继节点总函数
int i;
Node * child;
for(i = 0; i < 4; i++)
{
if(Canspread(**suc, i+1)) //判断某个方向上的子节点可否扩展
{
child = (Node *) malloc(sizeof(Node)); //扩展子节点
child->g = (*suc)->g +1; //算子节点的g值
child->parent = (*suc); //子节点父指针指向父节点
Spreadchild(child, i); //向该方向移动空格生成子节点
if(BelongProgram(&child, Open, Closed, goal, speed)) //判断子节点是否属

于OPEN或CLOSED表 并作出相应的处理
free(child);
}
}
}
///////////////////////扩展后继节点部分的函数-结束//////////////////////////////////

Node * Process(Lnode * org, Lnode * goal, Lstack * Open, Lstack * Closed, float speed)
{//总执行函数
while(1)
{
if((*Open)->next == NULL)return NULL; //判断OPEN表是否为空，为空则失败退出
Node * minf = Minf(Open); //从OPEN表中取出f值最小的节点
Putinto(minf, Closed); //将节点放入CLOSED表中
if(Equal(minf, *goal))return minf; //如果当前节点是目标节点，则成功退出
Spread(&minf, Open, Closed, **goal, speed); //当前节点不是目标节点时扩展当前节点的后继

节点
}
}

int Shownum(Node * result)
{//递归显示从初始状态到达目标状态的移动方法
if(result == NULL)return 0;
else
{
int n = Shownum(result->parent);
for(int i = 0; i < 3; i++)
{
printf("\n");
for(int j = 0; j < 3; j++)
{
if(result->data[i*3+j] != 0)
printf(" %d ",result->data[i*3+j]);
else printf(" ");
}
}
printf("\n");
return n+1;
}
}

后记：
日后，本BLOG将陆续实现所有经典的算法。是为记。完。

版权声明：
1、本人对本BLOG内所有任何文章和资料享有版权，转载，请注明作者本人，并以链接形式注明出处。
2、侵犯本人版权相关利益者，个人会在腾讯微博、CSDN迷你博客中永久追踪，给予谴责。
同时，保留追究法律责任的权利。向您的厚道致敬，谢谢。

July、二零一一年三月十日。