首先我们来看命题:
给定一个正整数n,需要输出一个长度为n的数组,数组元素是随机数,范围为0 – n-1,且元素不能重复。比如 n = 3 时,需要获取一个长度为3的数组,元素范围为0-2,
比如 0,2,1。
这个问题的通常解决方案就是设计一个 hashtable ,然后循环获取随机数,再到 hashtable 中找,如果hashtable 中没有这个数,则输出。下面给出这种算法的代码
public
static
int
[] GetRandomSequence0(int
total)
{
int
[] hashtable = new
int
[total];
int
[] output = new
int
[total];
Random random = new
Random();
for
(int
i = 0; i < total; i++)
{
int
num = random.Next(0, total);
while
(hashtable[num] > 0)
{
num = random.Next(0, total);
}
output[i] = num;
hashtable[num] = 1;
}
return
output;
}
.csharpcode, .csharpcode pre { font-size: small; color: black; font-family: consolas,"Courier New",courier,monospace; background-color: rgb(255, 255, 255); }.csharpcode pre { margin: 0em; }.csharpcode .rem { color: rgb(0, 128, 0); }.csharpcode .kwrd { color: rgb(0, 0, 255); }.csharpcode .str { color: rgb(0, 96, 128); }.csharpcode .op { color: rgb(0, 0, 192); }.csharpcode .preproc { color: rgb(204, 102, 51); }.csharpcode .asp { background-color: rgb(255, 255, 0); }.csharpcode .html { color: rgb(128, 0, 0); }.csharpcode .attr { color: rgb(255, 0, 0); }.csharpcode .alt { background-color: rgb(244, 244, 244); width: 100%; margin: 0em; }.csharpcode .lnum { color: rgb(96, 96, 96); }
代码很简单,从 0 到 total - 1 循环获取随机数,再去hashtable
中尝试匹配,如果这个数在hashtable中不存在,则输出,并把这个数在hashtable
中置1,否则循环尝试获取随机数,直到找到一个不在hashtable 中的数为止。这个算法的问题在于需要不断尝试获取随机数,在hashtable
接近满时,这个尝试失败的概率会越来越高。
那么有没有什么算法,不需要这样反复尝试吗?答案是肯定的。

如上图所示,我们设计一个顺序的数组,假设n = 4
第一轮,我们取 0 – 3 之间的随机数,假设为2,这时,我们把数组位置为2的数取出来输出,并把这个数从数组中删除,这时这个数组变成了

第二轮,我们再取 0-2 之间的随机数,假设为1,并把这个位置的数输出,同时把这个数从数组删除,以此类推,直到这个数组的长度为0。这时我们就可以得到一个随机的不重复的序列。
这个算法的好处是不需要用一个hashtable 来存储已获取的数字,不需要反复尝试。算法代码如下:
public
static
int
[] GetRandomSequence1(int
total)
{
List<int
> input = new
List<int
>();
for
(int
i = 0; i < total; i++)
{
input.Add(i);
}
List<int
> output = new
List<int
>();
Random random = new
Random();
int
end = total;
for
(int
i = 0; i < total; i++)
{
int
num = random.Next(0, end);
output.Add(input[num]);
input.RemoveAt(num);
end--;
}
return
output.ToArray();
}
.csharpcode, .csharpcode pre { font-size: small; color: black; font-family: consolas,"Courier New",courier,monospace; background-color: rgb(255, 255, 255); }.csharpcode pre { margin: 0em; }.csharpcode .rem { color: rgb(0, 128, 0); }.csharpcode .kwrd { color: rgb(0, 0, 255); }.csharpcode .str { color: rgb(0, 96, 128); }.csharpcode .op { color: rgb(0, 0, 192); }.csharpcode .preproc { color: rgb(204, 102, 51); }.csharpcode .asp { background-color: rgb(255, 255, 0); }.csharpcode .html { color: rgb(128, 0, 0); }.csharpcode .attr { color: rgb(255, 0, 0); }.csharpcode .alt { background-color: rgb(244, 244, 244); width: 100%; margin: 0em; }.csharpcode .lnum { color: rgb(96, 96, 96); }
这个算法把两个循环改成了一个循环,算法复杂度大大降低了,按说速度应该比第一个算法要快才对,然而现实往往超出我们的想象,当total =
100000 时,测试下来,第一个算法用时 44ms, 第二个用时 1038 ms ,慢了很多!这是为什么呢?问题的关键就在这个
input.RemoveAt
上了,我们知道如果要删除一个数组元素,我们需要把这个数组元素后面的所有元素都向前移动1,这个移动操作是非常耗时的,这个算法慢就慢在这里。到这里,
可能有人要说了,那我们不用数组,用链表,那删除不就很快了吗?没错,链表是能解决删除元素的效率问题,但查找的速度又大大降低了,无法像数组那样根据数
组元素下标直接定位到元素。所以用链表也是不行的。到这里似乎我们已经走到了死胡同,难道我们只能用hashtable
反复尝试来做吗?在看下面内容之前,请各位读者先思考5分钟。
…… 思考5分钟
算法就像一层窗户纸,隔着窗户纸,你永远无法知道里面是什么,一旦捅穿,又觉得非常简单。这个算法对于我,只用了2分钟时间想出来,因为我经常实现
算法,脑子里有一些模式,如果你的大脑还没有完成这种经验的积累,也许你要花比我长很多的时间来考虑这个问题,也许永远也找不到捅穿它的方法。不过不要
紧,我把这个方法公布出来,有了这个方法,你只需轻轻一动,一个完全不同的世界便出现在你的眼前。原来就这么简单……。
还是上面那个例子,假设 n = 4

第一轮,我们随机获得2时,我们不将 2 从数组中移除,而是将数组的最后一个元素移动到2的位置
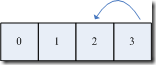
这时数组变成了

第二轮我们对 0-2 取随机数,这时数组可用的最后一个元素位置已经变成了2,而不是3。假设这时取到随机数为1
我们再把下标为2 的元素移动到下标1,这时数组变成了

以此类推,直到取出n个元素为止。
这个算法的优点是不需要用一个hashtable 来存储已获取的数字,不需要反复尝试,也不用像上一个算法那样删除数组元素,要做的只是每次把数组有效位置的最后一个元素移动到当前位置就可以了,这样算法的复杂度就降低为 O(n) ,速度大大提高。
经测试,在 n= 100000 时,这个算法的用时仅为7ms。
下面给出这个算法的实现代码
/// <summary>
/// Designed by eaglet
/// </summary>
/// <param name="total"></param>
/// <returns></returns>
public
static
int
[] GetRandomSequence2(int
total)
{
int
[] sequence = new
int
[total];
int
[] output = new
int
[total];
for
(int
i = 0; i < total; i++)
{
sequence[i] = i;
}
Random random = new
Random();
int
end = total - 1;
for
(int
i = 0; i < total; i++)
{
int
num = random.Next(0, end + 1);
output[i] = sequence[num];
sequence[num] = sequence[end];
end--;
}
return
output;
}
.csharpcode, .csharpcode pre { font-size: small; color: black; font-family: consolas,"Courier New",courier,monospace; background-color: rgb(255, 255, 255); }.csharpcode pre { margin: 0em; }.csharpcode .rem { color: rgb(0, 128, 0); }.csharpcode .kwrd { color: rgb(0, 0, 255); }.csharpcode .str { color: rgb(0, 96, 128); }.csharpcode .op { color: rgb(0, 0, 192); }.csharpcode .preproc { color: rgb(204, 102, 51); }.csharpcode .asp { background-color: rgb(255, 255, 0); }.csharpcode .html { color: rgb(128, 0, 0); }.csharpcode .attr { color: rgb(255, 0, 0); }.csharpcode .alt { background-color: rgb(244, 244, 244); width: 100%; margin: 0em; }.csharpcode .lnum { color: rgb(96, 96, 96); }
下面是n
等于1万,10万和100万时的测试数据,时间单位为毫秒。从测试数据看GetRandomSequence2的用时和n基本成正比,线性增长的,这个和
理论上的算法复杂度O(n)也是一致的,另外两个算法则随着n的增大,用时超过了线性增长。在1百万时,我的算法比用hashtable的算法要快10倍
以上。
| |
10000 |
100000 |
1000000 |
| GetRandomSequence0 |
5 |
44 |
1075 |
| GetRandomSequence1 |
11 |
1038 |
124205 |
| GetRandomSequence2 |
1 |
7 |
82 |
分享到:











相关推荐
与平方取中法相比,乘积取中法在随机数列长度和均匀性方面有所改善,但仍存在对初始值依赖较大的问题。 ##### 2. 移位法 移位法利用计算机擅长进行移位操作的特点,通过对初始值进行左移和右移操作,再进行逻辑加...
5. **算法分两部分**:包括随机数列生成器和记录器,前者负责生成不重复的随机数,后者负责记录并提供访问接口。 数据结构设计方面,文章提到了两个主要的数据结构:`shuffle_t`(顶层数据结构)和`random_t`(随机...
在IT领域,算法是解决问题的核心工具,而递归与分治策略、动态规划、贪心算法、回溯法、分支限界法以及随机化算法都是其中的重要组成部分。这些算法不仅适用于计算机科学,也在数据结构、优化问题和复杂计算中扮演着...
伪随机数生成器的核心在于一个数学算法,这个算法可以接受一个初始值(称为种子),然后根据该种子生成一串看似随机的数列。易语言中的伪随机数生成可能也遵循类似的机制。种子通常需要足够复杂,以确保生成的序列...
- **移位法**:运算速度快,但初始值选择不当可能导致较短的伪随机数列。 - **同余法(线性同余法)**:C语言中的标准方法,内存占用小,可以产生较长的周期,但同样对初始种子敏感。 5. **应用差异**:不同的...
伪随机数是由算法生成的数列,尽管它们看起来像是随机的,但实际上是由一个确定的算法决定的,可以重复生成,这与物理过程生成的真随机数有所不同。在计算机中,由于缺乏真正的随机性,我们通常使用伪随机数生成器...
伪随机函数(Pseudo-Random Function)并非真正的随机,而是通过特定的算法产生看起来随机的数列。这些数列具有不可预测性和统计均匀性,但实际上是确定性的,因为给定相同的种子(初始值),函数将始终产生相同的...
随机产生10000个浮点数,保存到a.txt文件中,再读取到内存中并分别用简单选择排序、冒泡排序、快速排序、希尔排序、归并排序、堆排序算法进行排序,显示排序过的数列的第1、10、100、1000、10000的具体数字和每个...
在计算机科学中,斐波那契数列常用于测试算法性能、数据结构优化,以及生成伪随机数等。 了解并掌握如何在Python中计算斐波那契数列的第n项,有助于提升编程能力,理解递归和迭代的概念,以及在实际问题中应用这些...
常见的伪随机数生成算法包括平方取中法、Fibonacci方法、线性同余法、混沌映射法和无理数变换法等。其中,线性同余法是一种经典的伪随机数生成算法,由Lehmer于1951年提出。线性同余法使用同余运算来产生随机数,其...
这个函数返回一个介于0(包含)和RAND_MAX(不包含)之间的伪随机整数。为了得到特定范围内的随机数,我们可以对`rand()`的结果进行适当处理,例如取模运算。同时,为了确保每次运行程序时生成相同的随机数序列,...
这个程序可能使用了伪随机数生成器,因为它可以提供无限的数列,而且在一定条件下具有可预测性和重复性,这在游戏环境中是非常实用的。随机数的范围可能是1到13,对应扑克牌的数字,也可能包括J(11)、Q(12)、K(13)...
8. **递推关系与动态规划**:在解决一些最优化问题时,动态规划算法利用递推关系(数列的一种)来避免重复计算,从而降低问题的复杂度。 9. **递归数列在密码学中的应用**:递归数列在密码学中具有应用,例如线性...
概率算法允许在计算过程中引入随机性,以提高效率或解决不可能精确解决的问题。例如,Monte Carlo方法、Las Vegas算法等。 十、近似算法 对于NP难问题,寻找精确解可能是不现实的,因此近似算法寻求接近最优解的...
冒泡排序是一种简单的排序算法,它重复地遍历待排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字...
C#通过Random类可以生成伪随机数,该类的构造函数可以接受一个种子值,不同种子值会生成不同的数列,确保每次运行程序都能得到不一样的结果。在点名程序中,可以使用当前时间作为种子,确保每次启动都产生新的点名...
4. **图论算法**:图是一种表示对象间关系的数据结构,图论算法包括最短路径算法(Dijkstra算法、Floyd-Warshall算法)、最小生成树算法(Prim算法、Kruskal算法)等。这些算法在网络设计、交通规划等领域有广泛应用...
在IT行业中,随机数生成是许多算法和应用的基础,如模拟、加密、游戏开发等。在C#编程语言中,生成随机数的过程涉及到System.Random类的使用。本项目"随机数自检-扑克检测"旨在通过一个实际的扑克牌检测案例来验证...