ه¤§éƒ¨هˆ†ن¸؛و‘که½•è‡ھwiki
آ
آ
و ‘çٹ¶ه›¾وک¯ن¸€ç§چو•°وچ®ç»“و„,ه®ƒوک¯ç”±n(n>=1)ن¸ھوœ‰é™گèٹ‚点组وˆگن¸€ن¸ھه…·وœ‰ه±‚و¬،ه…³ç³»çڑ„集هگˆم€‚وٹٹه®ƒهڈ«هپڑ“و ‘â€وک¯ه› ن¸؛ه®ƒçœ‹èµ·و¥هƒڈن¸€و£µه€’وŒ‚çڑ„و ‘,ن¹ںه°±وک¯è¯´ه®ƒوک¯و ¹وœن¸ٹ,而هڈ¶وœن¸‹çڑ„م€‚ه®ƒه…·وœ‰ن»¥ن¸‹çڑ„特点ï¼ڑ
- و¯ڈن¸ھèٹ‚点وœ‰é›¶ن¸ھوˆ–ه¤ڑن¸ھهگèٹ‚点;
- و²،وœ‰çˆ¶èٹ‚点çڑ„èٹ‚点称ن¸؛و ¹èٹ‚点;
- و¯ڈن¸€ن¸ھéو ¹èٹ‚点وœ‰ن¸”هڈھوœ‰ن¸€ن¸ھ父èٹ‚点;
- 除ن؛†و ¹èٹ‚点ه¤–,و¯ڈن¸ھهگèٹ‚点هڈ¯ن»¥هˆ†ن¸؛ه¤ڑن¸ھن¸چ相ن؛¤çڑ„هگو ‘ï¼›
آ
وœ¯è¯ï¼ڑ
- èٹ‚点çڑ„ه؛¦ï¼ڑن¸€ن¸ھèٹ‚点هگ«وœ‰çڑ„هگو ‘çڑ„ن¸ھو•°ç§°ن¸؛该èٹ‚点çڑ„ه؛¦ï¼›
- و ‘çڑ„ه؛¦ï¼ڑن¸€و£µو ‘ن¸ï¼Œوœ€ه¤§çڑ„èٹ‚点çڑ„ه؛¦ç§°ن¸؛و ‘çڑ„ه؛¦ï¼›
- هڈ¶èٹ‚点وˆ–终端èٹ‚点ï¼ڑه؛¦ن¸؛零çڑ„èٹ‚点;
- é终端èٹ‚点وˆ–هˆ†و”¯èٹ‚点ï¼ڑه؛¦ن¸چن¸؛零çڑ„èٹ‚点;
- 父ن؛²èٹ‚点وˆ–父èٹ‚点ï¼ڑè‹¥ن¸€ن¸ھèٹ‚点هگ«وœ‰هگèٹ‚点,هˆ™è؟™ن¸ھèٹ‚点称ن¸؛ه…¶هگèٹ‚点çڑ„父èٹ‚点;
- ه©هگèٹ‚点وˆ–هگèٹ‚点ï¼ڑن¸€ن¸ھèٹ‚点هگ«وœ‰çڑ„هگو ‘çڑ„و ¹èٹ‚点称ن¸؛该èٹ‚点çڑ„هگèٹ‚点;
- ه…„ه¼ںèٹ‚点ï¼ڑه…·وœ‰ç›¸هگŒçˆ¶èٹ‚点çڑ„èٹ‚点ن؛’称ن¸؛ه…„ه¼ںèٹ‚点;
- èٹ‚点çڑ„ه±‚و¬،ï¼ڑن»ژو ¹ه¼€ه§‹ه®ڑن¹‰èµ·ï¼Œو ¹ن¸؛第1ه±‚,و ¹çڑ„هگèٹ‚点ن¸؛第2ه±‚,ن»¥و¤ç±»وژ¨ï¼›
- و ‘çڑ„é«که؛¦وˆ–و·±ه؛¦ï¼ڑو ‘ن¸èٹ‚点çڑ„وœ€ه¤§ه±‚و¬،ï¼›
- ه ‚ه…„ه¼ںèٹ‚点ï¼ڑ父èٹ‚点هœ¨هگŒن¸€ه±‚çڑ„èٹ‚点ن؛’ن¸؛ه ‚ه…„ه¼ںï¼›
- èٹ‚点çڑ„祖ه…ˆï¼ڑن»ژو ¹هˆ°è¯¥èٹ‚点و‰€ç»ڈهˆ†و”¯ن¸ٹçڑ„و‰€وœ‰èٹ‚点;
- هگه™ï¼ڑن»¥وںگèٹ‚点ن¸؛و ¹çڑ„هگو ‘ن¸ن»»ن¸€èٹ‚点都称ن¸؛该èٹ‚点çڑ„هگه™م€‚
- و£®و—ï¼ڑç”±m(m>=0)و£µن؛’ن¸چ相ن؛¤çڑ„و ‘çڑ„集هگˆç§°ن¸؛و£®و—ï¼›
آ
و•°çڑ„ç§چç±»ï¼ڑ
- و— ه؛ڈو ‘ï¼ڑو ‘ن¸ن»»و„ڈèٹ‚点çڑ„هگèٹ‚点ن¹‹é—´و²،وœ‰é،؛ه؛ڈه…³ç³»ï¼Œè؟™ç§چو ‘称ن¸؛و— ه؛ڈو ‘,ن¹ں称ن¸؛è‡ھç”±و ‘ï¼›
- وœ‰ه؛ڈو ‘ï¼ڑو ‘ن¸ن»»و„ڈèٹ‚点çڑ„هگèٹ‚点ن¹‹é—´وœ‰é،؛ه؛ڈه…³ç³»ï¼Œè؟™ç§چو ‘称ن¸؛وœ‰ه؛ڈو ‘ï¼›
-
ن؛Œهڈ‰و ‘ï¼ڑو¯ڈن¸ھèٹ‚点وœ€ه¤ڑهگ«وœ‰ن¸¤ن¸ھهگو ‘çڑ„و ‘称ن¸؛ن؛Œهڈ‰و ‘ï¼›
- ه®Œه…¨ن؛Œهڈ‰و ‘ï¼ڑه¯¹ن؛ژن¸€é¢—ن؛Œهڈ‰و ‘,هپ‡è®¾ه…¶و·±ه؛¦ن¸؛d(d>1)م€‚除ن؛†ç¬¬dه±‚ه¤–,ه…¶ه®ƒهگ„ه±‚çڑ„èٹ‚点و•°ç›®ه‡ه·²è¾¾وœ€ه¤§ه€¼ï¼Œن¸”第dه±‚و‰€وœ‰èٹ‚点ن»ژه·¦هگ‘هڈ³è؟ç»هœ°ç´§ه¯†وژ’هˆ—,è؟™و ·çڑ„ن؛Œهڈ‰و ‘被称ن¸؛ه®Œه…¨ن؛Œهڈ‰و ‘ï¼›
- و»،ن؛Œهڈ‰و ‘ï¼ڑه¯¹ن؛ژن¸ٹè؟°çڑ„ه®Œه…¨ن؛Œهڈ‰و ‘,ه¦‚وœهژ»وژ‰ه…¶ç¬¬dه±‚çڑ„و‰€وœ‰èٹ‚点,那ن¹ˆه‰©ن¸‹çڑ„部هˆ†ه°±و„وˆگن¸€ن¸ھو»،ن؛Œهڈ‰و ‘(و¤و—¶è¯¥و»،ن؛Œهڈ‰و ‘çڑ„و·±ه؛¦ن¸؛d-1);
- éœچه¤«و›¼و ‘ï¼ڑه¸¦وƒè·¯ه¾„وœ€çںçڑ„ن؛Œهڈ‰و ‘称ن¸؛ه“ˆه¤«و›¼و ‘وˆ–وœ€ن¼کن؛Œهڈ‰و ‘ï¼›
- Bو ‘
-
ن؛Œهڈ‰و ‘ï¼ڑو¯ڈن¸ھèٹ‚点وœ€ه¤ڑهگ«وœ‰ن¸¤ن¸ھهگو ‘çڑ„و ‘称ن¸؛ن؛Œهڈ‰و ‘ï¼›
آ
ن؛Œهڈ‰و ‘وک¯و¯ڈن¸ھèٹ‚点وœ€ه¤ڑوœ‰ن¸¤ن¸ھهگو ‘çڑ„و ‘结و„م€‚é€ڑه¸¸هگو ‘被称ن½œâ€œه·¦هگو ‘â€ï¼ˆleft subtree)ه’Œâ€œهڈ³هگو ‘â€ï¼ˆright subtree)م€‚ن؛Œهڈ‰و ‘ه¸¸è¢«ç”¨ن؛ژه®çژ°ن؛Œهڈ‰وں¥و‰¾و ‘ه’Œن؛Œهڈ‰ه †م€‚
ن؛Œهڈ‰و ‘çڑ„و¯ڈن¸ھ结点至ه¤ڑهڈھوœ‰ن؛Œو£µهگو ‘(ن¸چهکهœ¨ه؛¦ه¤§ن؛ژ2çڑ„结点),ن؛Œهڈ‰و ‘çڑ„هگو ‘وœ‰ه·¦هڈ³ن¹‹هˆ†ï¼Œو¬،ه؛ڈن¸چèƒ½é¢ ه€’م€‚ن؛Œهڈ‰و ‘çڑ„第iه±‚至ه¤ڑوœ‰ ن¸ھ结点;و·±ه؛¦ن¸؛kçڑ„ن؛Œهڈ‰و ‘至ه¤ڑوœ‰
ن¸ھ结点;و·±ه؛¦ن¸؛kçڑ„ن؛Œهڈ‰و ‘至ه¤ڑوœ‰ ن¸ھ结点;ه¯¹ن»»ن½•ن¸€و£µن؛Œهڈ‰و ‘T,ه¦‚وœه…¶ç»ˆç«¯ç»“点و•°ن¸؛
ن¸ھ结点;ه¯¹ن»»ن½•ن¸€و£µن؛Œهڈ‰و ‘T,ه¦‚وœه…¶ç»ˆç«¯ç»“点و•°ن¸؛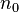 ,ه؛¦ن¸؛2çڑ„结点و•°ن¸؛
,ه؛¦ن¸؛2çڑ„结点و•°ن¸؛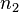 ,هˆ™
,هˆ™ م€‚
م€‚
ن¸€و£µو·±ه؛¦ن¸؛k,ن¸”وœ‰ ن¸ھèٹ‚点称ن¹‹ن¸؛و»،ن؛Œهڈ‰و ‘ï¼›و·±ه؛¦ن¸؛k,وœ‰nن¸ھèٹ‚点çڑ„ن؛Œهڈ‰و ‘,ه½“ن¸”ن»…ه½“ه…¶و¯ڈن¸€ن¸ھèٹ‚点都ن¸ژو·±ه؛¦ن¸؛kçڑ„و»،ن؛Œهڈ‰و ‘ن¸ï¼Œه؛ڈهڈ·ن¸؛1至nçڑ„èٹ‚点ه¯¹ه؛”و—¶ï¼Œç§°ن¹‹ن¸؛ه®Œه…¨ن؛Œهڈ‰و ‘م€‚(简هچ•è¯´ï¼Œه°±وک¯و¯ڈن¸€ه±‚都وک¯و»،çڑ„ن؛Œهڈ‰و ‘ن¸؛و»،ن؛Œهڈ‰و ‘ï¼›هڈھوœ‰وœ€هگژن¸€ه±‚ن¸چو»،,ه¹¶ن¸”وœ€هگژن¸€ه±‚çڑ„èٹ‚点都وک¯هچ وچ®ن؛†ه·¦è¾¹çڑ„è؟ç»ن½چç½®çڑ„ن؛Œهڈ‰و ‘ن¸؛ه®Œه…¨ن؛Œهڈ‰و ‘)
ن¸ھèٹ‚点称ن¹‹ن¸؛و»،ن؛Œهڈ‰و ‘ï¼›و·±ه؛¦ن¸؛k,وœ‰nن¸ھèٹ‚点çڑ„ن؛Œهڈ‰و ‘,ه½“ن¸”ن»…ه½“ه…¶و¯ڈن¸€ن¸ھèٹ‚点都ن¸ژو·±ه؛¦ن¸؛kçڑ„و»،ن؛Œهڈ‰و ‘ن¸ï¼Œه؛ڈهڈ·ن¸؛1至nçڑ„èٹ‚点ه¯¹ه؛”و—¶ï¼Œç§°ن¹‹ن¸؛ه®Œه…¨ن؛Œهڈ‰و ‘م€‚(简هچ•è¯´ï¼Œه°±وک¯و¯ڈن¸€ه±‚都وک¯و»،çڑ„ن؛Œهڈ‰و ‘ن¸؛و»،ن؛Œهڈ‰و ‘ï¼›هڈھوœ‰وœ€هگژن¸€ه±‚ن¸چو»،,ه¹¶ن¸”وœ€هگژن¸€ه±‚çڑ„èٹ‚点都وک¯هچ وچ®ن؛†ه·¦è¾¹çڑ„è؟ç»ن½چç½®çڑ„ن؛Œهڈ‰و ‘ن¸؛ه®Œه…¨ن؛Œهڈ‰و ‘)
ن¸ژو ‘ن¸چهگŒï¼Œو ‘çڑ„结点ن¸ھو•°è‡³ه°‘ن¸؛1,而ن؛Œهڈ‰و ‘çڑ„结点ن¸ھو•°هڈ¯ن»¥ن¸؛0ï¼›و ‘ن¸ç»“点çڑ„وœ€ه¤§ه؛¦و•°و²،وœ‰é™گهˆ¶ï¼Œè€Œن؛Œهڈ‰و ‘结点çڑ„وœ€ه¤§ه؛¦و•°ن¸؛2ï¼›و ‘çڑ„结点و— ه·¦م€پهڈ³ن¹‹هˆ†ï¼Œè€Œن؛Œهڈ‰و ‘çڑ„结点وœ‰ه·¦م€پهڈ³ن¹‹هˆ†م€‚

آ
è®؟é—®ن؛Œهڈ‰و ‘çڑ„و–¹و³•
آ
ه‰چ(ه…ˆ)ه؛ڈم€پن¸ه؛ڈم€پهگژه؛ڈéپچهژ†

آ ن؛Œهڈ‰وں¥و‰¾و ‘(英è¯ï¼ڑBinary Search Tree),ن¹ں称ن؛Œهڈ‰وگœç´¢و ‘م€پوœ‰ه؛ڈن؛Œهڈ‰و ‘(英è¯ï¼ڑordered binary tree),وژ’ه؛ڈن؛Œهڈ‰و ‘(英è¯ï¼ڑsorted binary tree),وک¯وŒ‡ن¸€و£µç©؛و ‘وˆ–者ه…·وœ‰ن¸‹هˆ—و€§è´¨çڑ„ن؛Œهڈ‰و ‘ï¼ڑ
- è‹¥ن»»و„ڈèٹ‚点çڑ„ه·¦هگو ‘ن¸چç©؛,هˆ™ه·¦هگو ‘ن¸ٹو‰€وœ‰ç»“点çڑ„ه€¼ه‡ه°ڈن؛ژوˆ–ç‰ن؛ژه®ƒçڑ„و ¹ç»“点çڑ„ه€¼ï¼›
- ن»»و„ڈèٹ‚点çڑ„هڈ³هگو ‘ن¸چç©؛,هˆ™هڈ³هگو ‘ن¸ٹو‰€وœ‰ç»“点çڑ„ه€¼ه‡ه¤§ن؛ژه®ƒçڑ„و ¹ç»“点çڑ„ه€¼ï¼›
- ن»»و„ڈèٹ‚点çڑ„ه·¦م€پهڈ³هگو ‘ن¹ںهˆ†هˆ«ن¸؛ن؛Œهڈ‰وں¥و‰¾و ‘م€‚
- و²،وœ‰é”®ه€¼ç›¸ç‰çڑ„èٹ‚点(英è¯ï¼ڑno duplicate nodes)م€‚
ن؛Œهڈ‰وں¥و‰¾و ‘相و¯”ن؛ژه…¶ن»–و•°وچ®ç»“و„çڑ„ن¼کهٹ؟هœ¨ن؛ژوں¥و‰¾م€پوڈ’ه…¥çڑ„و—¶é—´ه¤چو‚ه؛¦è¾ƒن½ژم€‚ن¸؛O(log n)م€‚ن؛Œهڈ‰وں¥و‰¾و ‘وک¯هں؛ç،€و€§و•°وچ®ç»“و„,用ن؛ژو„ه»؛و›´ن¸؛وٹ½è±،çڑ„و•°وچ®ç»“و„,ه¦‚集هگˆم€پmultisetم€په…³èپ”و•°ç»„ç‰م€‚
ن؛Œهڈ‰وں¥و‰¾و ‘çڑ„وں¥و‰¾è؟‡ç¨‹ه’Œو¬،ن¼کن؛Œهڈ‰و ‘ç±»ن¼¼ï¼Œé€ڑه¸¸é‡‡هڈ–ن؛Œهڈ‰é“¾è،¨ن½œن¸؛ن؛Œهڈ‰وں¥و‰¾و ‘çڑ„هکه‚¨ç»“و„م€‚ن¸ه؛ڈéپچهژ†ن؛Œهڈ‰وں¥و‰¾و ‘هڈ¯ه¾—هˆ°ن¸€ن¸ھه…³é”®ه—çڑ„وœ‰ه؛ڈه؛ڈهˆ—,ن¸€ن¸ھو— ه؛ڈه؛ڈهˆ—هڈ¯ن»¥é€ڑè؟‡و„é€ ن¸€و£µن؛Œهڈ‰وں¥و‰¾و ‘هڈکوˆگن¸€ن¸ھوœ‰ه؛ڈه؛ڈهˆ—,و„é€ و ‘çڑ„è؟‡ç¨‹هچ³ن¸؛ه¯¹و— ه؛ڈه؛ڈهˆ—è؟›è،Œوں¥و‰¾çڑ„è؟‡ç¨‹م€‚و¯ڈو¬،وڈ’ه…¥çڑ„و–°çڑ„结点都وک¯ن؛Œهڈ‰وں¥و‰¾و ‘ن¸ٹو–°çڑ„هڈ¶هگ结点,هœ¨è؟›è،Œوڈ’ه…¥و“چن½œو—¶ï¼Œن¸چه؟…移هٹ¨ه…¶ه®ƒç»“点,هڈھ需و”¹هٹ¨وںگن¸ھ结点çڑ„وŒ‡é’ˆï¼Œç”±ç©؛هڈکن¸؛éç©؛هچ³هڈ¯م€‚وگœç´¢م€پوڈ’ه…¥م€پهˆ 除çڑ„ه¤چو‚ه؛¦ç‰ن؛ژو ‘é«ک,وœںوœ› ,وœ€هڈ
,وœ€هڈ (و•°هˆ—وœ‰ه؛ڈ,و ‘退هŒ–وˆگç؛؟و€§è،¨ï¼‰م€‚
(و•°هˆ—وœ‰ه؛ڈ,و ‘退هŒ–وˆگç؛؟و€§è،¨ï¼‰م€‚
虽然ن؛Œهڈ‰وں¥و‰¾و ‘çڑ„وœ€هڈو•ˆçژ‡وک¯O(n),ن½†ه®ƒو”¯وŒپهٹ¨و€پوں¥è¯¢,ن¸”وœ‰ه¾ˆه¤ڑو”¹è؟›ç‰ˆçڑ„ن؛Œهڈ‰وں¥و‰¾و ‘هڈ¯ن»¥ن½؟و ‘é«کن¸؛ ,ه¦‚SBT,AVLو ‘,ç؛¢é»‘و ‘ç‰.و•…ن¸چه¤±ن¸؛ن¸€ç§چه¥½çڑ„هٹ¨و€پوں¥و‰¾و–¹و³•.
,ه¦‚SBT,AVLو ‘,ç؛¢é»‘و ‘ç‰.و•…ن¸چه¤±ن¸؛ن¸€ç§چه¥½çڑ„هٹ¨و€پوں¥و‰¾و–¹و³•.
آ
ه †ï¼ˆè‹±è¯ï¼ڑheap),وک¯è®،ç®—وœ؛科ه¦ن¸ن¸€ç±»ç‰¹و®ٹçڑ„و•°وچ®ç»“و„çڑ„ç»ں称م€‚ه †é€ڑه¸¸وک¯ن¸€ن¸ھهڈ¯ن»¥è¢«çœ‹هپڑن¸€و£µو ‘çڑ„و•°ç»„ه¯¹è±،م€‚هœ¨éکںهˆ—ن¸ï¼Œè°ƒه؛¦ç¨‹ه؛ڈهڈچه¤چوڈگهڈ–éکںهˆ—ن¸ç¬¬ن¸€ن¸ھن½œن¸ڑه¹¶è؟گè،Œï¼Œه› ن¸؛ه®é™…وƒ…ه†µن¸وںگن؛›و—¶é—´è¾ƒçںçڑ„ن»»هٹ،ه°†ç‰ه¾…ه¾ˆé•؟و—¶é—´و‰چ能结وں,وˆ–者وںگن؛›ن¸چçںه°ڈ,ن½†ه…·وœ‰é‡چè¦پو€§çڑ„ن½œن¸ڑ,هگŒو ·ه؛”ه½“ه…·وœ‰ن¼که…ˆوƒم€‚ه †هچ³ن¸؛解ه†³و¤ç±»é—®é¢ک设è®،çڑ„ن¸€ç§چو•°وچ®ç»“و„م€‚
ه †çڑ„ه®çژ°é€ڑè؟‡و„é€ ن؛Œهڈ‰ه †ï¼ˆbinary heap),ه®ن¸؛ن؛Œهڈ‰و ‘çڑ„ن¸€ç§چ;由ن؛ژه…¶ه؛”用çڑ„و™®éپچو€§ï¼Œه½“ن¸چهٹ é™گه®ڑو—¶ï¼Œه‡وŒ‡è¯¥و•°وچ®ç»“و„çڑ„è؟™ç§چه®çژ°م€‚è؟™ç§چو•°وچ®ç»“و„ه…·وœ‰ن»¥ن¸‹و€§è´¨م€‚
- ن»»و„ڈèٹ‚点ه°ڈن؛ژه®ƒçڑ„و‰€وœ‰هگژ裔,وœ€ه°ڈه…ƒهœ¨ه †çڑ„و ¹ن¸ٹ(ه †ه؛ڈو€§ï¼‰م€‚
- ه †و€»وک¯ن¸€و£µه®Œه…¨و ‘م€‚
آ
ه°†و ¹èٹ‚点وœ€ه¤§çڑ„ه †هڈ«هپڑوœ€ه¤§ه †وˆ–ه¤§و ¹ه †ï¼Œو ¹èٹ‚点وœ€ه°ڈçڑ„ه †هڈ«هپڑوœ€ه°ڈه †وˆ–ه°ڈو ¹ه †م€‚ه¸¸è§پçڑ„ه †وœ‰ن؛Œهڈ‰ه †م€پو–گو³¢é‚£ه¥‘ه †ç‰م€‚
آ
و“چن½œï¼ڑ
1.وڈ’ه…¥èٹ‚点ï¼ڑن»ژه †ه°¾éƒ¨وڈ’ه…¥م€‚然هگژè°ƒو•´é،؛ه؛ڈ,ن»ژه †ه°¾ه¼€ه§‹é€گن¸ھه’Œه…¶و ¹ه…ƒç´ و¯”较,ه¹¶è°ƒو•´م€‚
2.هˆ 除èٹ‚点ï¼ڑهˆ 除و ¹èٹ‚点م€‚然هگژ,وٹٹه †هکه‚¨çڑ„وœ€هگژé‚£ن¸ھèٹ‚点移هˆ°ه،«هœ¨و ¹èٹ‚点ه¤„م€‚ه†چن»ژن¸ٹ而ن¸‹è°ƒو•´çˆ¶èٹ‚点ن¸ژه®ƒçڑ„هگèٹ‚点ï¼ڑه¯¹ن؛ژوœ€ه¤§ه †ï¼Œçˆ¶èٹ‚点ه¦‚وœه°ڈن؛ژه…·وœ‰وœ€ه¤§ه€¼çڑ„هگèٹ‚点,هˆ™ن؛¤وچ¢ن؛Œè€…م€‚直至ه½“ه‰چèٹ‚点ن¸ژه®ƒçڑ„هگèٹ‚点و»،足ه †و€§è´¨ن¸؛و¢م€‚










相ه…³وژ¨èچگ
ه¸¸è§پçڑ„و•°وچ®ç»“و„وœ‰و•°ç»„م€پ链è،¨م€پو ˆم€پéکںهˆ—م€پو ‘م€په›¾ç‰م€‚ ن؛Œم€پç؛؟و€§و•°وچ®ç»“و„ 1. و•°ç»„ï¼ڑو•°ç»„وک¯وœ€هں؛ç،€çڑ„و•°وچ®ç»“و„,ه®ƒوک¯ن¸€ç»„相هگŒç±»ه‹ه…ƒç´ çڑ„وœ‰ه؛ڈ集هگˆï¼Œé€ڑè؟‡ن¸‹و ‡è؟›è،Œè®؟é—®م€‚و•°ç»„çڑ„ن¼ک点وک¯è®؟é—®é€ںه؛¦ه؟«ï¼Œن½†وڈ’ه…¥ه’Œهˆ 除و“چن½œو•ˆçژ‡ن½ژم€‚ 2...
ن¸œهچ—ه¤§ه¦çڑ„é«کç؛§و•°وچ®ç»“و„课程ن¸ï¼Œه¦ç”ںه’Œو•™ه¸ˆن»¬ن¸€èµ·و•´çگ†ه½’ç؛³ن؛†ه¤ڑن¸ھé«کç؛§و•°وچ®ç»“و„هڈٹه…¶ه†…هœ¨èپ”系,ه¯¹è؟™ن؛›ه†…ه®¹çڑ„و·±ه…¥çگ†è§£وœ‰هٹ©ن؛ژه¦ç”ںو›´ه¥½هœ°وژŒوڈ،و•°وچ®ç»“و„çڑ„و ¸ه؟ƒçں¥è¯†ن»¥هڈٹه¦‚ن½•هœ¨ه®é™…é—®é¢کن¸é€‰و‹©هگˆé€‚çڑ„و•°وچ®ç»“و„م€‚ هœ¨و•°وچ®ç»“و„çڑ„...
"ن¸¥ç‰ˆو•°وچ®ç»“و„é‡چ点ه½’ç؛³"وک¯ن¸€ن¸ھن¸“门针ه¯¹è؟™ن¸€ن¸»é¢کçڑ„资و–™ï¼Œه®ƒن»¥Wordو–‡و،£çڑ„ه½¢ه¼ڈوڈگن¾›ن؛†ه¯¹و•°وچ®ç»“و„ه…³é”®و¦‚ه؟µçڑ„و€»ç»“ه’Œوڈگ炼م€‚è؟™ن»½èµ„و–™ه¯¹ن؛ژه¦ن¹ 者و¥è¯´ه…·وœ‰ه¾ˆé«کçڑ„ن»·ه€¼ï¼Œه› ن¸؛ه®ƒهڈ¯ن»¥ه¸®هٹ©ن»–ن»¬ه؟«é€ںçگ†è§£ه’ŒوژŒوڈ،و•°وچ®ç»“و„çڑ„ه…³é”®çں¥è¯†ç‚¹م€‚...
و•°وچ®ç»“و„ه¸¸è§پ笔试é¢کو±‡و€» وœ¬èµ„و؛گو‘کè¦پن؟،وپ¯ن¸ï¼Œوˆ‘ن»¬ه°†ه¯¹و•°وچ®ç»“و„ه¸¸è§پ笔试é¢کè؟›è،Œو±‡و€»ï¼Œو¶µç›–ç®—و³•çڑ„هں؛وœ¬و¦‚ه؟µم€پو•°وچ®ç»“و„çڑ„ه®ڑن¹‰م€پç؛؟و€§ç»“و„ه’Œéç؛؟و€§ç»“و„م€پç؛؟و€§è،¨çڑ„é،؛ه؛ڈهکه‚¨ç»“و„م€پé،؛ه؛ڈè،¨çڑ„وڈ’ه…¥ه’Œهˆ 除è؟گç®—م€پو ˆهڈٹه…¶هں؛وœ¬è؟گç®—ç‰...
"و•°وچ®ç»“و„ه¤چن¹ é‡چ点ه½’ç؛³ç¬”è®°[و¸…هچژن¸¥è”ڑو•ڈ版]" و•°وچ®ç»“و„وک¯ن¸€é—¨هں؛ç،€çگ†è®؛课,و¶‰هڈٹهˆ°è®،ç®—وœ؛科ه¦ه’Œوٹ€وœ¯çڑ„ه¤ڑن¸ھ领هںںم€‚ن؛†è§£و•°وچ®ç»“و„çڑ„çں¥è¯†ç‚¹ه¯¹è®،ç®—وœ؛ن¸“ن¸ڑه¦ç”ںو¥è¯´وک¯éه¸¸é‡چè¦پçڑ„م€‚وœ¬و–‡ه°†ه¯¹و•°وچ®ç»“و„çڑ„ç« èٹ‚结و„ه’Œé‡چ点ه†…ه®¹è؟›è،Œه½’ç؛³...
### و•°وچ®ç»“و„è€ƒç ”ه¤چن¹ é‡چ点ه½’ç؛³ #### ن¸€م€پو•°وچ®ç»“و„çڑ„ç« èٹ‚结و„هڈٹé‡چ点و„وˆگ و•°وچ®ç»“و„وک¯ن¸€é—¨هں؛ç،€ن¸”é‡چè¦پçڑ„è®،ç®—وœ؛科ه¦è¯¾ç¨‹ï¼Œه®ƒن¸چن»…و¶‰هڈٹهˆ°هگ„ç§چو•°وچ®ç»„织ه½¢ه¼ڈçڑ„çگ†è§£ن¸ژè؟گ用,è؟کو¶‰هڈٹهˆ°ن؛†ç®—و³•çڑ„设è®،ن¸ژهˆ†وگم€‚هœ¨è€ƒç ”ه¤‡è€ƒéک¶و®µï¼Œ...
و•°وچ®ç»“و„وک¯è®،ç®—وœ؛科ه¦ن¸çڑ„و ¸ه؟ƒè¯¾ç¨‹ï¼Œه®ƒوژ¢è®¨ه¦‚ن½•وœ‰و•ˆهœ°هکه‚¨ه’Œو“چن½œو•°وچ®م€‚ن¸¥è”ڑو•ڈو•™وژˆçڑ„م€ٹو•°وچ®ç»“و„م€‹وک¯و¸…هچژه¤§ه¦ه‡؛版çڑ„ç»ڈه…¸و•™وگ,针ه¯¹Cè¯è¨€ç¼–ه†™م€‚وœ¬èµ„و–™çڑ„é‡چ点ه½’ç؛³و—¨هœ¨ه¸®هٹ©ه¦ç”ںçگ†è§£ه’ŒوژŒوڈ،ه…³é”®و¦‚ه؟µم€‚ و•°وچ®ç»“و„ن¸»è¦پهˆ†ن¸؛...
وœ¬و–‡ه°†é’ˆه¯¹â€œو•°وچ®ç»“و„ه¤چن¹ é‡چ点ه½’ç؛³ï¼ˆé€‚ن؛ژو¸…هچژن¸¥ç‰ˆو•™وگ)â€è؟›è،Œè¯¦ç»†çڑ„解وگ,و—¨هœ¨ه¸®هٹ©ه¤‡è€ƒè€…وکژç،®ه¤چن¹ è¦پ点م€‚ 首ه…ˆï¼Œو•°وچ®ç»“و„çڑ„ç« èٹ‚结و„é€ڑه¸¸هˆ†ن¸؛ï¼ڑو¦‚è®؛م€پç؛؟و€§è،¨م€پو ˆه’Œéکںهˆ—م€پن¸²م€په¤ڑç»´و•°ç»„ه’Œه¹؟ن¹‰è،¨م€پو ‘ه’Œن؛Œهڈ‰و ‘م€په›¾م€پوں¥و‰¾...
### و•°وچ®ç»“و„ه¤چن¹ é‡چ点ه½’ç؛³ و•°وچ®ç»“و„وک¯è®،ç®—وœ؛科ه¦ن¸çڑ„ن¸€ن¸ھو ¸ه؟ƒو¦‚ه؟µï¼Œه®ƒن¸»è¦پç ”ç©¶ن¸چهگŒو•°وچ®ç»„织و–¹ه¼ڈهڈٹه…¶هœ¨ç®—و³•è®¾è®،ن¸çڑ„ه؛”用م€‚وœ¬و¬،ه½’ç؛³و€»ç»“ن؛†و•°وچ®ç»“و„ه¦ن¹ ن¸çڑ„ه‡ ن¸ھه…³é”®çں¥è¯†ç‚¹ï¼Œو—¨هœ¨ه¸®هٹ©é‚£ن؛›و£هœ¨ه‡†ه¤‡è€ƒè¯•وˆ–ه¤چن¹ çڑ„هگŒه¦و›´ه¥½...
ن¸¥è”ڑو•ڈو•™وژˆçڑ„م€ٹو•°وچ®ç»“و„م€‹و•™وگوک¯è¯¥é¢†هںںçڑ„ç»ڈه…¸ن¹‹ن½œï¼Œوœ¬ه¤چن¹ é‡چ点ه½’ç؛³ç¬”è®°ن¸»è¦پé’ˆه¯¹è¯¥و•™وگçڑ„ه†…ه®¹è؟›è،Œن؛†وڈگ炼ه’Œو€»ç»“م€‚ 首ه…ˆï¼Œو•°وچ®ç»“و„çڑ„ç« èٹ‚结و„و¶µç›–ن؛†و¦‚è®؛م€پç؛؟و€§è،¨م€پو ˆه’Œéکںهˆ—م€پن¸²م€په¤ڑç»´و•°ç»„ه’Œه¹؟ن¹‰è،¨م€پو ‘ه’Œن؛Œهڈ‰و ‘م€په›¾م€پ...
ن¸¥è”ڑو•ڈو•™وژˆçڑ„م€ٹو•°وچ®ç»“و„م€‹وک¯è¯¥é¢†هںںçڑ„ç»ڈه…¸و•™وگ,وœ¬ç¯‡و–‡ç« ه°†é’ˆه¯¹è¯¥و•™وگçڑ„é‡چ点è؟›è،Œه½’ç؛³م€‚ 首ه…ˆï¼Œوˆ‘ن»¬è¦پن؛†è§£و•°وچ®ç»“و„çڑ„ç« èٹ‚و„وˆگم€‚ه®ƒé€ڑه¸¸هŒ…و‹¬و¦‚è®؛م€پç؛؟و€§è،¨م€پو ˆه’Œéکںهˆ—م€پن¸²م€په¤ڑç»´و•°ç»„ه’Œه¹؟ن¹‰è،¨م€پو ‘ه’Œن؛Œهڈ‰و ‘م€په›¾م€پوں¥و‰¾م€پوژ’ه؛ڈ...
م€گ电هگ科وٹ€ه¤§ه¦820و•°وچ®ç»“و„考ç؛²è€ƒç‚¹ه½’ç؛³م€‘ هœ¨è½¯ن»¶ه¼€هڈ‘领هںں,و•°وچ®ç»“و„وک¯è‡³ه…³é‡چè¦پçڑ„هں؛ç،€çں¥è¯†ï¼Œه®ƒو¶‰هڈٹه¦‚ن½•é«کو•ˆهœ°ç»„织ه’Œو“چن½œو•°وچ®م€‚وœ¬è€ƒç؛²ن¸»è¦پو¶µç›–ن؛†و•°وچ®ç»“و„هڈٹç®—و³•çڑ„相ه…³و¦‚ه؟µم€پ逻辑结و„ن¸ژهکه‚¨ç»“و„م€پç®—و³•ç‰¹و€§ن»¥هڈٹç؛؟و€§è،¨...
م€ٹJavaو•°وچ®ç»“و„ه½’ç؛³م€‹ و•°وچ®ç»“و„وک¯è®،ç®—وœ؛科ه¦çڑ„هں؛çں³ï¼Œه®ƒوک¯ç ”究éو•°ه€¼è®،ç®—é—®é¢کن¸و•°وچ®ه…ƒç´ ن¹‹é—´ه…³ç³»çڑ„ه¦ç§‘م€‚هœ¨ç¨‹ه؛ڈ设è®،ن¸ï¼Œو•°وچ®ç»“و„ن¸ژç®—و³•وک¯ه¯†ن¸چهڈ¯هˆ†çڑ„,ه®ƒن»¬ه…±هگŒو„وˆگن؛†ç¨‹ه؛ڈçڑ„هں؛ç،€م€‚و•°وچ®ç»“و„ه®ڑن¹‰ن؛†ن¸€ن¸ھو•°وچ®ه…ƒç´ 集هگˆï¼Œ...
م€گو•°وچ®ç»“و„ه¸¸ç”¨ç®—و³•ه½’ç؛³م€‘ هœ¨è®،ç®—وœ؛科ه¦ن¸ï¼Œو•°وچ®ç»“و„ه’Œç®—و³•وک¯è§£ه†³é—®é¢کçڑ„هں؛ç،€ï¼Œه…¶ن¸وژ’ه؛ڈç®—و³•وک¯و•°وچ®ه¤„çگ†ن¸ن¸چهڈ¯وˆ–ç¼؛çڑ„ن¸€éƒ¨هˆ†م€‚وœ¬و–‡ن¸»è¦پوژ¢è®¨ن¸¤ç§چه¸¸è§پçڑ„وژ’ه؛ڈç®—و³•ï¼ڑه†’و³،وژ’ه؛ڈه’Œوڈ’ه…¥وژ’ه؛ڈم€‚ **ه†’و³،وژ’ه؛ڈ** وک¯ن¸€ç§چ简هچ•ç›´è§‚çڑ„...
وœ¬و–‡ه°†ه¯¹و•°وچ®ç»“و„ه¤چن¹ çڑ„é‡چ点çں¥è¯†è؟›è،Œè¯¦ç»†ه½’ç؛³ï¼Œه¸®هٹ©ه¤‡è€ƒè€…é«کو•ˆوژŒوڈ،ه…³é”®و¦‚ه؟µم€‚ 首ه…ˆï¼Œو•°وچ®ç»“و„çڑ„ç« èٹ‚و„وˆگé€ڑه¸¸هŒ…و‹¬و¦‚è®؛م€پç؛؟و€§è،¨م€پو ˆه’Œéکںهˆ—م€پن¸²م€په¤ڑç»´و•°ç»„ه’Œه¹؟ن¹‰è،¨م€پو ‘ه’Œن؛Œهڈ‰و ‘م€په›¾م€پوں¥و‰¾م€پوژ’ه؛ڈم€په†…هکç®،çگ†ï¼ˆه†…وژ’ه’Œه¤–وژ’...
هœ¨è؟™ن¸ھ201310913232و•°وچ®ç»“و„ه½’ç؛³çڑ„ه®éھŒوٹ¥ه‘ٹن¸ï¼Œه¦ç”ںé€ڑè؟‡ن¸€ç³»هˆ—çڑ„ه®éھŒو¥çگ†è§£ه’ŒوژŒوڈ،و•°وچ®ç»“و„çڑ„هں؛وœ¬و¦‚ه؟µه’Œو“چن½œم€‚ن»¥ن¸‹وک¯هگ„ه®éھŒçڑ„ن¸»è¦پçں¥è¯†ç‚¹ï¼ڑ ه®éھŒن¸€ï¼ڑé،؛ه؛ڈè،¨هں؛وœ¬و“چن½œçڑ„ه®çژ° هœ¨è؟™ن¸ھه®éھŒن¸ï¼Œه¦ç”ںه¦ن¹ ن؛†é،؛ه؛ڈè،¨çڑ„ه»؛ç«‹م€پهڈ–...