最普通的字符串匹配算法就不记了,简单贴一下代码
-
int
strstr(
char
*sub, char
* str)
{
-
int
i=0
;
-
char
*p=str, *q=sub;
-
while
(
*(
p+i)
!='\0
'
&&*(
q+i)
!='\0
'
)
{
-
if
(
*(
q+i)
==*(
p+i)
)
-
i++;
-
else
{
-
p++;
-
i=0
;
-
}
-
}
-
if
(
*(
q+i)
=='\0
'
)
-
return
p-str;
-
return
-1
;
-
}
下面说说我理解的KMP算法,与普通匹配算法不一样的是,KMP算法在子串匹配失效的时候,下一步并不是重新从子串的头部开始匹配,而是根据一下next函数计算出下一步应该从子串的什么部位开始匹配。举个例子更容易说明

红色为失效位置, '^'表示的当前是指针位置,'~'表示此次匹配A串开始的位置。
若是普通的匹配算法,当失效时,C串指针要回溯到头部,A串指针也要回溯到'~'的下一位。也就是下一步应该是从A的第二字符(e.g. 'b')和C的开头(e.g. 'a')开始匹配。如此循环

直到找到A串中的某一个位置可以匹配C串。
然而从上面的匹配过程中,可以发现A和B的蓝色部分是第一步中已经确认匹配过的,上面四步的匹配其实可以看作是蓝色部分的前半段与后半段在进行比
较,而且前三步在蓝色部分就已经匹配失效了,所以这些比较是无谓的,因为它与父串A无关的,是属于子串C本身的信息。只有第四步才涉及了与父串A中的字符
('c')的比较
KMP算法正是利用这一点,它事先利用子串本身的信息就计算出当某一次匹配失效时,下一次应该继续匹配的位置。也就是当C串在最后一个'b
'匹配失效时,它省略了前三步(1,2,3)无谓的匹配,下一步比较将在'd'与'c'之间进行。这样父串A无需回溯,C串用一个next函数决定它将回溯的位置。所以next函数至关重要,也是这个算法的关键。
从上面的分析可以知道next函数是子串C本身的性质决定的
假设子串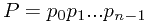
next(j)=k(k>=0): 当P的第 j+1个字符 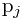 匹配失败时, 在父串指针不回溯的情况下,下一步将与
匹配失败时, 在父串指针不回溯的情况下,下一步将与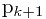 比较。next(j)的函数计算可以表达为
比较。next(j)的函数计算可以表达为
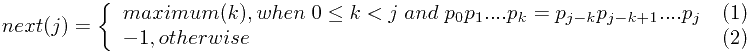
当next(j)=k (k>=0)时,子串指针回溯到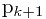 的位置,父串指针不变;
的位置,父串指针不变;
当next(j)=-1时,子串指针回溯到头,父串指针前进一步;
在设计计算next值的程序的时候,我们没有必要每一步都去计算maximum(k),可以用递归方式来做
举个例子
假设子串为P:"abacabab
", 且我们将要求的是'b
'的next值, e.g. next[7]
假设next[0~6]均为已知: next[0]=-1, next[1]=-1 , next[2]=0 , next[3]=-1 , next[4]=0 , next[5]=1 ,next[6]=2
"aba
caba
b"
next[6]=2可以说明P[0~2](蓝)与P[4~6](红)是一样的
要求next[7]的值,我们可以找前6位("abacaba")中最长的前半段与后半段相等的子串,然后比较前半段子串的下一位是否和P[7]相
等。在这个例子中, P[0~next[6]](e.g. P[0~2])就是这样的子串,接下来我们比较 c 和
b也就是P[next[6]+1]('c')和P[7]('b').
- 若相等则 next[7] = next[6]+1
- 若不等, 我们进一步找更短的前半段与后半段相等的子串,因为aba
和aba
是一样的, 要找'aba
caba
'中比'abc'短的这样的子串,相当于找'aba
' 中的next[2]值是一样的.也就是next[next[6]]的值。然后再比较P[next[next[6]]+1]和P[7]是否等,若不等则继续找更短的这样子串
在上的例子中 P[next[6]+1]=P[3]('c') ,与P[7]('b')不相等, 但是 P[next[next[6]]+1] = P[next[2]+1] = P[1]('b'), 与P[7]('b')相等
最后可以得到next[7] = next[next[6]]+1 = next[2]+1= 1;
计算next值的代码:
-
void
calnext(
char
* P, int
next[
]
)
{
-
next[
0
]
= -1
; //第一个元素的next总是-1, 因为根据(1) , 我们并找不到一个k比j=0小
-
for
(
int
i=1
; i<strlen(
P)
; i++)
{
-
int
k = next[
i-1
]
; //因为采用递归的方法, 为了计算next[i], 先记录下next[i-1] 而且假设next[i-1]已知
-
while
(
P[
k+1
]
!=P[
i]
&&k>=0
)
{
// 递归
-
k = next[
k]
;
-
}
-
if
(
P[
k+1
]
==P[
i]
)
//如果相等而结束, 则找到一对长度为k的前缀字串和后缀字串
-
next[
i]
= k+1
; //增加了一个相同项
-
else
-
next[
i]
= -1
; //其他情况
-
}
-
}
匹配的代码:
-
int
find(
char
*T, char
* pat)
{
-
int
n = strlen(
pat)
;
-
int
*next = new int
[
n]
;
-
calnet(
pat, next)
;
-
char
*p=T, *q=pat;
-
int
i=0
;
-
while
(
*p!='\0
'
&&(
*(
q+i)
!='\0
'
)
)
{
-
if
(
*p==*(
q+i)
)
{
-
p++;
-
i++;
-
}
else
{
-
if
(
i==0
)
-
p++;
-
else
-
i = next[
i-1
]
+1
;
-
}
-
}
-
if
(
*(
q+i)
=='\0
'
)
-
return
p-T-n;
-
else
-
return
-1
;
-
}
记录一下自己理解的KMP以免以后自己都忘记当时怎么理解的。
分享到:








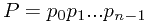
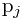 匹配失败时, 在父串指针不回溯的情况下,下一步将与
匹配失败时, 在父串指针不回溯的情况下,下一步将与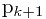 比较。next(j)的函数计算可以表达为
比较。next(j)的函数计算可以表达为


相关推荐
以Snort 2.0为例,这是一种开源的NIDS系统,通过对不同字符串匹配算法进行评测,确定在实际应用中哪些算法更有效。研究结果显示,在高速网络环境中,高效的字符串匹配算法对于提高系统的性能至关重要。 #### 六、...
8. **KMP算法**:一种高效的字符串匹配算法,用于在一个字符串中查找另一个字符串的出现位置,避免了不必要的回溯。 9. **Rabin-Karp算法**:另一种字符串匹配算法,使用哈希函数加速查找过程。 10. **Manacher's ...
4. **Z-Algorithm**:一种在线的字符串匹配算法,可以同时找到所有子串的所有非重叠匹配。Z-数组是核心,记录了每个位置最长前后缀的长度,使得查找过程变得高效。 5. **动态规划法**:在字符串问题中,动态规划常...
KMP(Knuth-Morris-Pratt)算法是一种在文本串中高效地查找子串的字符串匹配算法。它由唐纳德·克努斯、詹姆斯·莫里斯和维尔莫特·普拉特在1970年提出。KMP算法避免了在匹配过程中不必要的字符比较,通过构建一个...
2. **朴素匹配算法**:最基础的字符串匹配方法,从主字符串的第一个字符开始,逐个比较字符,如果遇到不匹配则回溯。虽然简单,但效率较低,时间复杂度为O(n*m),n为主字符串长度,m为模式字符串长度。 3. **KMP...
KMP(字符串匹配),Trie树(字典树),manacher(最长回文子串) 算法思想 代码 经典题目
8. **Z-Algorithm**:一种在线字符串匹配算法,可以在O(n)的时间内找出字符串的所有子串位置。 9. **滑动窗口**:在处理字符串中的最大/最小值问题时,滑动窗口的概念常常被用到,例如查找最长的无重复字符子串、最...
1. **KMP算法**(Knuth-Morris-Pratt Algorithm):KMP算法是一种用于在一个字符串(主串)中查找给定模式串的有效方法,它避免了在匹配过程中不必要的回溯。通过构造部分匹配表,KMP可以在主串中发现模式串的匹配...
KMP算法是一种高效的字符串匹配算法,用于在一个较大的字符串(通常称为模板串)中查找一个较小的字符串(称为子串)的所有出现位置。该算法的核心在于利用了子串自身的部分匹配性质,从而避免了在匹配过程中不必要...
在IT领域,字符串查找是一项基础且重要的操作,广泛应用于各种编程场景中,如文本处理、数据检索、模式匹配等。本文将围绕“字符串查找”这一主题,深入探讨其概念、应用以及实现方法,并通过分析提供的代码片段来...
KMP算法是一种字符串匹配算法,用于判断模式串在主串中出现的次数。该算法的优点是可以在不移动主串的情况下进行匹配,提高了匹配效率。 KMP算法的思想是,通过计算模式串的next数组,来记录模式串中的每个字符所...
字符串匹配算法通常用于文本处理,但其原理也可应用于曲线对比。动态规划(如KMP或Rabin-Karp算法)提供了一种有效的方式,通过比较两个序列的子序列来查找相似性。在曲线对比中,我们可以将曲线视为“字符串”,每...
- **BF算法**(Brute Force算法)是最简单的字符串匹配算法,它通过逐个字符比较目标串S和模式串T来寻找匹配。如果当前字符不匹配,模式串回溯到起始位置,目标串向前移动一位。这种方法效率较低,因为存在大量不必...
字符串匹配算法的任务是在文本T中找出模式P的所有出现位置。该问题有几个常用的表示符号,包括n和m分别表示模式P和文本T的长度,Σ表示字符集,Pi表示P中的第i个字符,而x,y,z表示字符串。举一个简单的例子:如果T=...
Z算法是一种线性时间复杂度的字符串匹配算法,由日本科学家Mori和Ogura提出。它能在O(n)的时间内计算出一个字符串的所有子串的最长前缀与后缀的最大长度,从而快速进行模式匹配。Z算法的基本思想是动态构建一个Z...
KMP算法是一种高效的字符串匹配算法,它可以避免在出现不匹配时回溯过多。这个算法通过构建部分匹配表,减少不必要的比较,提高搜索效率。 在这些代码实现中,你不仅可以学习到数据结构的基本操作,还能了解到如何...
除了动态规划,还有其他算法如KMP(Knuth-Morris-Pratt)算法和Z算法等,这些算法能够在线性时间复杂度内解决最长公共子串问题。这些方法通过对字符串的特定部分进行预处理,能够在不回溯的情况下快速跳过不可能构成...
BM算法是一种字符串查找的算法,其匹配速度要远远优于简单的字符匹配;在模式串较长的情况下,其效率高于KMP算法
- **KMP算法**:一种高效的字符串匹配算法,避免了不必要的回溯,时间复杂度为O(n + m)。 - **Boyer-Moore算法**:利用坏字符规则和好后缀规则提高匹配效率,尤其适用于长模式串。 - **Rabin-Karp算法**:使用...
此外,字符串处理算法如KMP、Rabin-Karp和Boyer-Moore,是文本搜索和模式匹配的关键。这些算法能有效地提高在大量文本中查找特定模式的速度。 随机化技术,如随机化排序(如快速排序的随机化版本)和概率数据结构...