1.В дёүи§’еү–еҲҶдёҺDelaunayеү–еҲҶзҡ„е®ҡд№ү
В В В В В еҰӮдҪ•жҠҠдёҖдёӘж•ЈзӮ№йӣҶеҗҲеү–еҲҶжҲҗдёҚеқҮеҢҖзҡ„дёүи§’еҪўзҪ‘ж јпјҢиҝҷе°ұжҳҜж•ЈзӮ№йӣҶзҡ„дёүи§’еү–еҲҶй—®йўҳпјҢж•ЈзӮ№йӣҶзҡ„дёүи§’еү–еҲҶпјҢеҜ№ж•°еҖјеҲҶжһҗд»ҘеҸҠеӣҫеҪўеӯҰжқҘиҜҙпјҢйғҪжҳҜжһҒдёәйҮҚиҰҒзҡ„дёҖйЎ№йў„еӨ„зҗҶжҠҖжңҜгҖӮиҜҘй—®йўҳеӣҫзӨәеҰӮдёӢпјҡ
1.1.дёүи§’еү–еҲҶе®ҡд№ү
В В В гҖҗе®ҡд№үгҖ‘дёүи§’еү–еҲҶпјҡеҒҮи®ҫVжҳҜдәҢз»ҙе®һж•°еҹҹдёҠзҡ„жңүйҷҗзӮ№йӣҶпјҢиҫ№eжҳҜз”ұзӮ№йӣҶдёӯзҡ„зӮ№дҪңдёәз«ҜзӮ№жһ„жҲҗзҡ„е°Ғй—ӯзәҝж®ө, Eдёәeзҡ„йӣҶеҗҲгҖӮйӮЈд№ҲиҜҘзӮ№йӣҶVзҡ„дёҖдёӘдёүи§’еү–еҲҶT=(V,E)жҳҜдёҖдёӘе№ійқўеӣҫGпјҢиҜҘе№ійқўеӣҫж»Ўи¶іжқЎд»¶пјҡ
В В В 1.йҷӨдәҶз«ҜзӮ№пјҢе№ійқўеӣҫдёӯзҡ„иҫ№дёҚеҢ…еҗ«зӮ№йӣҶдёӯзҡ„д»»дҪ•зӮ№гҖӮ
В В В 2.жІЎжңүзӣёдәӨиҫ№гҖӮ
В В В 3.е№ійқўеӣҫдёӯжүҖжңүзҡ„йқўйғҪжҳҜдёүи§’йқўпјҢдё”жүҖжңүдёүи§’йқўзҡ„еҗҲйӣҶжҳҜж•ЈзӮ№йӣҶVзҡ„еҮёеҢ…гҖӮ
1.2.В Delaunayдёүи§’еү–еҲҶзҡ„е®ҡд№ү
В В В еңЁе®һйҷ…дёӯиҝҗз”Ёзҡ„жңҖеӨҡзҡ„дёүи§’еү–еҲҶжҳҜDelaunayдёүи§’еү–еҲҶпјҢе®ғжҳҜдёҖз§Қзү№ж®Ҡзҡ„дёүи§’еү–еҲҶгҖӮе…Ҳд»ҺDelaunayиҫ№иҜҙиө·пјҡ
В В В гҖҗе®ҡд№үгҖ‘Delaunayиҫ№пјҡеҒҮи®ҫEдёӯзҡ„дёҖжқЎиҫ№eпјҲдёӨдёӘз«ҜзӮ№дёәa,bпјүпјҢeиӢҘж»Ўи¶ідёӢеҲ—жқЎд»¶пјҢеҲҷз§°д№ӢдёәDelaunayиҫ№пјҡеӯҳеңЁдёҖдёӘеңҶз»ҸиҝҮa,bдёӨзӮ№пјҢеңҶеҶ…(жіЁж„ҸжҳҜеңҶеҶ…пјҢеңҶдёҠжңҖеӨҡдёүзӮ№е…ұеңҶ)дёҚеҗ«зӮ№йӣҶVдёӯд»»дҪ•е…¶д»–зҡ„зӮ№пјҢиҝҷдёҖзү№жҖ§еҸҲз§°з©әеңҶзү№жҖ§гҖӮ
В В В гҖҗе®ҡд№үгҖ‘Delaunayдёүи§’еү–еҲҶпјҡеҰӮжһңзӮ№йӣҶVзҡ„дёҖдёӘдёүи§’еү–еҲҶTеҸӘеҢ…еҗ«Delaunayиҫ№пјҢйӮЈд№ҲиҜҘдёүи§’еү–еҲҶз§°дёәDelaunayдёүи§’еү–еҲҶгҖӮ
1.3.Delaunayдёүи§’еү–еҲҶзҡ„еҮҶеҲҷ
В В В иҰҒж»Ўи¶іDelaunayдёүи§’еү–еҲҶзҡ„е®ҡд№үпјҢеҝ…йЎ»з¬ҰеҗҲдёӨдёӘйҮҚиҰҒзҡ„еҮҶеҲҷпјҡ
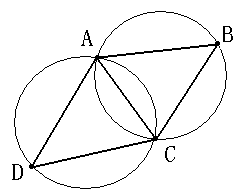
В В В 1гҖҒз©әеңҶзү№жҖ§пјҡDelaunayдёүи§’зҪ‘жҳҜе”ҜдёҖзҡ„пјҲд»»ж„ҸеӣӣзӮ№дёҚиғҪе…ұеңҶпјүпјҢеңЁDelaunayдёүи§’еҪўзҪ‘дёӯд»»дёҖдёүи§’еҪўзҡ„еӨ–жҺҘеңҶиҢғеӣҙеҶ…дёҚдјҡжңүе…¶е®ғзӮ№еӯҳеңЁгҖӮеҰӮдёӢеӣҫжүҖзӨәпјҡ
В
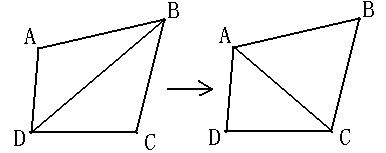
В В В 2гҖҒжңҖеӨ§еҢ–жңҖе°Ҹи§’зү№жҖ§пјҡеңЁж•ЈзӮ№йӣҶеҸҜиғҪеҪўжҲҗзҡ„дёүи§’еү–еҲҶдёӯпјҢDelaunayдёүи§’еү–еҲҶжүҖеҪўжҲҗзҡ„дёүи§’еҪўзҡ„жңҖе°Ҹи§’жңҖеӨ§гҖӮд»ҺиҝҷдёӘж„Ҹд№үдёҠи®ІпјҢDelaunay дёүи§’зҪ‘жҳҜвҖңжңҖжҺҘиҝ‘дәҺ规еҲҷеҢ–зҡ„вҖңзҡ„дёүи§’зҪ‘гҖӮе…·дҪ“зҡ„иҜҙжҳҜжҢҮеңЁдёӨдёӘзӣёйӮ»зҡ„дёүи§’еҪўжһ„жҲҗеҮёеӣӣиҫ№еҪўзҡ„еҜ№и§’зәҝпјҢеңЁзӣёдә’дәӨжҚўеҗҺпјҢе…ӯдёӘеҶ…и§’зҡ„жңҖе°Ҹи§’дёҚеҶҚеўһеӨ§гҖӮеҰӮдёӢеӣҫжүҖзӨәпјҡ
В
1.4.Delaunayдёүи§’еү–еҲҶзҡ„зү№жҖ§
В В В д»ҘдёӢжҳҜDelaunayеү–еҲҶжүҖе…·еӨҮзҡ„дјҳејӮзү№жҖ§пјҡ
В В В 1.жңҖжҺҘиҝ‘пјҡд»ҘжңҖиҝ‘дёҙзҡ„дёүзӮ№еҪўжҲҗдёүи§’еҪўпјҢдё”еҗ„зәҝж®ө(дёүи§’еҪўзҡ„иҫ№)зҡҶдёҚзӣёдәӨгҖӮ
В В В 2.е”ҜдёҖжҖ§пјҡдёҚи®әд»ҺеҢәеҹҹдҪ•еӨ„ејҖе§Ӣжһ„е»әпјҢжңҖз»ҲйғҪе°Ҷеҫ—еҲ°дёҖиҮҙзҡ„з»“жһңгҖӮ
В В В 3.жңҖдјҳжҖ§пјҡд»»ж„ҸдёӨдёӘзӣёйӮ»дёүи§’еҪўеҪўжҲҗзҡ„еҮёеӣӣиҫ№еҪўзҡ„еҜ№и§’зәҝеҰӮжһңеҸҜд»Ҙдә’жҚўзҡ„иҜқпјҢйӮЈд№ҲдёӨдёӘдёүи§’еҪўе…ӯдёӘеҶ…и§’дёӯжңҖе°Ҹзҡ„и§’еәҰдёҚдјҡеҸҳеӨ§гҖӮ
В В В 4.жңҖ规еҲҷпјҡеҰӮжһңе°Ҷдёүи§’зҪ‘дёӯзҡ„жҜҸдёӘдёүи§’еҪўзҡ„жңҖе°Ҹи§’иҝӣиЎҢеҚҮеәҸжҺ’еҲ—пјҢеҲҷDelaunayдёүи§’зҪ‘зҡ„жҺ’еҲ—еҫ—еҲ°зҡ„ж•°еҖјжңҖеӨ§гҖӮ
В В В 5.еҢәеҹҹжҖ§пјҡж–°еўһгҖҒеҲ йҷӨгҖҒ移еҠЁжҹҗдёҖдёӘйЎ¶зӮ№ж—¶еҸӘдјҡеҪұе“Қдёҙиҝ‘зҡ„дёүи§’еҪўгҖӮ
В В В 6.е…·жңүеҮёеӨҡиҫ№еҪўзҡ„еӨ–еЈіпјҡдёүи§’зҪ‘жңҖеӨ–еұӮзҡ„иҫ№з•ҢеҪўжҲҗдёҖдёӘеҮёеӨҡиҫ№еҪўзҡ„еӨ–еЈігҖӮ
1.5.еұҖйғЁжңҖдјҳеҢ–еӨ„зҗҶ
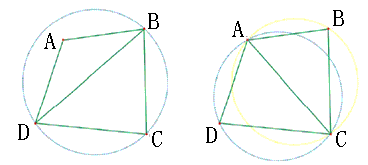
В В В зҗҶи®әдёҠдёәдәҶжһ„йҖ Delaunayдёүи§’зҪ‘пјҢLawsonжҸҗеҮәзҡ„еұҖйғЁдјҳеҢ–иҝҮзЁӢLOP(Local Optimization Procedure)пјҢдёҖиҲ¬дёүи§’зҪ‘з»ҸиҝҮLOPеӨ„зҗҶпјҢеҚіеҸҜзЎ®дҝқжҲҗдёәDelaunayдёүи§’зҪ‘пјҢе…¶еҹәжң¬еҒҡжі•еҰӮдёӢжүҖзӨәпјҡ
В В В 1.е°ҶдёӨдёӘе…·жңүе…ұеҗҢиҫ№зҡ„дёүи§’еҪўеҗҲжҲҗдёҖдёӘеӨҡиҫ№еҪўгҖӮ
В В В 2.д»ҘжңҖеӨ§з©әеңҶеҮҶеҲҷдҪңжЈҖжҹҘпјҢзңӢ其第еӣӣдёӘйЎ¶зӮ№жҳҜеҗҰеңЁдёүи§’еҪўзҡ„еӨ–жҺҘеңҶд№ӢеҶ…гҖӮ
В В В 3.еҰӮжһңеңЁпјҢдҝ®жӯЈеҜ№и§’зәҝеҚіе°ҶеҜ№и§’зәҝеҜ№и°ғпјҢеҚіе®ҢжҲҗеұҖйғЁдјҳеҢ–иҝҮзЁӢзҡ„еӨ„зҗҶгҖӮ
В В В LOPеӨ„зҗҶиҝҮзЁӢеҰӮдёӢеӣҫжүҖзӨәпјҡ
2.Delaunayеү–еҲҶзҡ„з®—жі•
В В В Delaunayеү–еҲҶжҳҜдёҖз§Қдёүи§’еү–еҲҶзҡ„ж ҮеҮҶпјҢе®һзҺ°е®ғжңүеӨҡз§Қз®—жі•гҖӮ
2.1.Lawsonз®—жі•
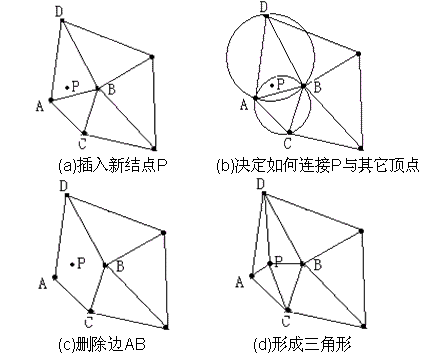
В В В йҖҗзӮ№жҸ’е…Ҙзҡ„Lawsonз®—жі•жҳҜLawsonеңЁ1977е№ҙжҸҗеҮәзҡ„пјҢиҜҘз®—жі•жҖқи·Ҝз®ҖеҚ•пјҢжҳ“дәҺзј–зЁӢе®һзҺ°гҖӮеҹәжң¬еҺҹзҗҶдёәпјҡйҰ–е…Ҳе»әз«ӢдёҖдёӘеӨ§зҡ„дёүи§’еҪўжҲ–еӨҡиҫ№еҪўпјҢжҠҠ жүҖжңүж•°жҚ®зӮ№еҢ…еӣҙиө·жқҘпјҢеҗ‘е…¶дёӯжҸ’е…ҘдёҖзӮ№пјҢиҜҘзӮ№дёҺеҢ…еҗ«е®ғзҡ„дёүи§’еҪўдёүдёӘйЎ¶зӮ№зӣёиҝһпјҢеҪўжҲҗдёүдёӘж–°зҡ„дёүи§’еҪўпјҢ然еҗҺйҖҗдёӘеҜ№е®ғ们иҝӣиЎҢз©әеӨ–жҺҘеңҶжЈҖжөӢпјҢеҗҢж—¶з”ЁLawsonи®ҫи®Ў зҡ„еұҖйғЁдјҳеҢ–иҝҮзЁӢLOPиҝӣиЎҢдјҳеҢ–пјҢеҚійҖҡиҝҮдәӨжҚўеҜ№и§’зәҝзҡ„ж–№жі•жқҘдҝқиҜҒжүҖеҪўжҲҗзҡ„дёүи§’зҪ‘дёәDelaunayдёүи§’зҪ‘гҖӮ
В В В дёҠиҝ°еҹәдәҺж•ЈзӮ№зҡ„жһ„зҪ‘з®—жі•зҗҶи®әдёҘеҜҶгҖҒе”ҜдёҖжҖ§еҘҪпјҢзҪ‘ж јж»Ўи¶із©әеңҶзү№жҖ§пјҢиҫғдёәзҗҶжғігҖӮз”ұе…¶йҖҗзӮ№жҸ’ е…Ҙзҡ„жһ„зҪ‘иҝҮзЁӢеҸҜзҹҘпјҢйҒҮеҲ°йқһDelaunayиҫ№ж—¶пјҢйҖҡиҝҮеҲ йҷӨи°ғж•ҙпјҢеҸҜд»Ҙжһ„йҖ еҪўжҲҗж–°зҡ„Delaunayиҫ№гҖӮеңЁе®ҢжҲҗжһ„зҪ‘еҗҺпјҢеўһеҠ ж–°зӮ№ж—¶пјҢж— йңҖеҜ№жүҖжңүзҡ„зӮ№иҝӣиЎҢйҮҚж–° жһ„зҪ‘пјҢеҸӘйңҖеҜ№ж–°зӮ№зҡ„еҪұе“Қдёүи§’еҪўиҢғеӣҙиҝӣиЎҢеұҖйғЁиҒ”зҪ‘пјҢдё”еұҖйғЁиҒ”зҪ‘зҡ„ж–№жі•з®ҖеҚ•жҳ“иЎҢгҖӮеҗҢж ·пјҢзӮ№зҡ„еҲ йҷӨгҖҒ移еҠЁд№ҹеҸҜеҝ«йҖҹеҠЁжҖҒең°иҝӣиЎҢгҖӮдҪҶеңЁе®һйҷ…еә”з”ЁеҪ“дёӯпјҢиҝҷз§Қжһ„зҪ‘з®—жі•еҪ“ зӮ№йӣҶиҫғеӨ§ж—¶жһ„зҪ‘йҖҹеәҰд№ҹиҫғж…ўпјҢеҰӮжһңзӮ№йӣҶиҢғеӣҙжҳҜйқһеҮёеҢәеҹҹжҲ–иҖ…еӯҳеңЁеҶ…зҺҜпјҢеҲҷдјҡдә§з”ҹйқһжі•дёүи§’еҪўгҖӮ
2.2.Bowyer-Watsonз®—жі•
В В В Lawsonз®—жі•зҡ„еҹәжң¬жӯҘйӘӨжҳҜпјҡ
В В В 1гҖҒжһ„йҖ дёҖдёӘи¶…зә§дёүи§’еҪўпјҢеҢ…еҗ«жүҖжңүж•ЈзӮ№пјҢж”ҫе…Ҙдёүи§’еҪўй“ҫиЎЁгҖӮ
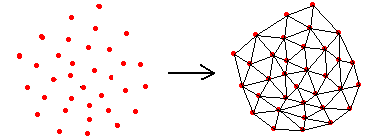
В В В 2гҖҒе°ҶзӮ№йӣҶдёӯзҡ„ж•ЈзӮ№дҫқж¬ЎжҸ’е…ҘпјҢеңЁдёүи§’еҪўй“ҫиЎЁдёӯжүҫеҮәе…¶еӨ–жҺҘеңҶеҢ…еҗ«жҸ’е…ҘзӮ№зҡ„дёүи§’еҪўпјҲз§°дёәиҜҘзӮ№зҡ„еҪұе“Қдёүи§’еҪўпјүпјҢеҲ йҷӨеҪұе“Қдёүи§’еҪўзҡ„е…¬е…ұиҫ№пјҢе°ҶжҸ’е…ҘзӮ№еҗҢеҪұе“Қдёүи§’еҪўзҡ„е…ЁйғЁйЎ¶зӮ№иҝһжҺҘиө·жқҘпјҢд»ҺиҖҢе®ҢжҲҗдёҖдёӘзӮ№еңЁDelaunayдёүи§’еҪўй“ҫиЎЁдёӯзҡ„жҸ’е…ҘгҖӮ
В В В 3гҖҒж №жҚ®дјҳеҢ–еҮҶеҲҷеҜ№еұҖйғЁж–°еҪўжҲҗзҡ„дёүи§’еҪўиҝӣиЎҢдјҳеҢ–гҖӮе°ҶеҪўжҲҗзҡ„дёүи§’еҪўж”ҫе…ҘDelaunayдёүи§’еҪўй“ҫиЎЁгҖӮ
В В В 4гҖҒеҫӘзҺҜжү§иЎҢдёҠиҝ°з¬¬2жӯҘпјҢзӣҙеҲ°жүҖжңүж•ЈзӮ№жҸ’е…Ҙе®ҢжҜ•гҖӮ
В В В иҝҷдёҖз®—жі•зҡ„е…ій”®зҡ„第2жӯҘеӣҫзӨәеҰӮдёӢпјҡ
жң¬ж–ҮжқҘиҮӘCSDNеҚҡе®ўпјҢhttp://www.cnblogs.com/RenLiQQ/archive/2008/02/06/1065399.html
еҲҶдә«еҲ°пјҡ












зӣёе…іжҺЁиҚҗ
е°Өе…¶жҳҜDelaunayдёүи§’еү–еҲҶпјҢз”ұдәҺе…¶зӢ¬зү№жҖ§пјҢе…ідәҺзӮ№йӣҶзҡ„еҫҲеӨҡз§ҚеҮ дҪ•еӣҫйғҪе’ҢDelaunayдёүи§’еү–еҲҶзӣёе…іпјҢеҰӮVoronoiеӣҫпјҢEMSTж ‘пјҢGabrielеӣҫзӯүгҖӮDelaunayдёүи§’еү–еҲҶжңүжңҖеӨ§еҢ–жңҖе°Ҹи§’пјҢвҖңжңҖжҺҘиҝ‘дәҺ规еҲҷеҢ–зҡ„вҖңзҡ„дёүи§’зҪ‘е’Ңе”ҜдёҖжҖ§пјҲд»»ж„ҸеӣӣзӮ№дёҚ...
Delaunayдёүи§’еү–еҲҶз®—жі• Delaunayдёүи§’еү–еҲҶз®—жі•жҳҜдёҖз§Қеёёз”Ёзҡ„зҰ»ж•ЈзӮ№з”ҹжҲҗдёүи§’зҪ‘з»ңзҡ„з®—жі•пјҢдё»иҰҒз”ЁдәҺи®Ўз®—жңәеӣҫеҪўеӯҰгҖҒең°зҗҶдҝЎжҒҜзі»з»ҹгҖҒи®Ўз®—жңәи§Ҷи§үзӯүйўҶеҹҹгҖӮиҜҘз®—жі•зҡ„еҺҹзҗҶеҸҜд»ҘеҲҶдёәдёүжӯҘпјҡеҮёеҢ…з”ҹжҲҗгҖҒзҺҜеҲҮиҫ№з•Ңжі•еҮёеҢ…дёүи§’еү–еҲҶе’ҢзҰ»ж•Јзҡ„...
Delaunayдёүи§’еү–еҲҶз®—жі• 1. дёүи§’еү–еҲҶдёҺDelaunayеү–еҲҶзҡ„е®ҡд№ү еҰӮдҪ•жҠҠдёҖдёӘж•ЈзӮ№йӣҶеҗҲеү–еҲҶжҲҗдёҚеқҮеҢҖзҡ„дёүи§’еҪўзҪ‘ж јпјҢиҝҷе°ұжҳҜж•ЈзӮ№йӣҶзҡ„дёүи§’еү–еҲҶй—®йўҳпјҢж•ЈзӮ№йӣҶзҡ„дёүи§’еү–еҲҶпјҢеҜ№ж•°еҖјеҲҶжһҗд»ҘеҸҠеӣҫеҪўеӯҰжқҘиҜҙпјҢйғҪжҳҜжһҒдёәйҮҚиҰҒзҡ„дёҖйЎ№йў„еӨ„зҗҶжҠҖжңҜгҖӮ ...
з”Ёpython3.6е®һзҺ°delaunayдёүи§’еү–еҲҶз®—жі•пјҢиҜ»е…Ҙеӯҳжңүеқҗж Үзҡ„csvж–Ү件пјҢи®Ўз®—еҮәз»“жһңз”ЁTkinterеә“жҳҫзӨәгҖӮ
并иЎҢеү–еҲҶз®—жі•иғҪеӨҹжҳҫи‘—жҸҗеҚҮи®Ўз®—йҖҹеәҰпјҢиҖҢдәӨзӮ№жҸ’е…Ҙз®—жі•еҲҷе……еҲҶиҖғиҷ‘дәҶзү№еҫҒзәҝзҡ„еҪұе“Қеҹҹд»ҘеҸҠDelaunayдёүи§’еҪўи§„еҲҷзҡ„иҫ№з•ҢжқЎд»¶пјҢзЎ®дҝқеңЁж»Ўи¶іе…ЁеұҖDelaunayдёүи§’еү–еҲҶзҡ„еҗҢж—¶пјҢжҸ’е…Ҙзҡ„зӮ№жңҖе°‘пјҢеҜ№еҺҹжңүзҡ„зҪ‘ж јеҪұе“ҚжңҖе°ҸгҖӮ #### е…ій”®иҜҚ ...
Delaunayдёүи§’еү–еҲҶз®—жі•еңЁз§‘еӯҰи®Ўз®—еҸҜи§ҶеҢ–гҖҒжңүйҷҗе…ғеҲҶжһҗгҖҒең°еӯҰеҲҶжһҗгҖҒең°зҗҶдҝЎжҒҜзі»з»ҹзӯүйўҶеҹҹжңүзқҖе№ҝжіӣзҡ„еә”з”ЁгҖӮ Delaunayдёүи§’еү–еҲҶз®—жі•зҡ„е®һзҺ°ж–№жі•дё»иҰҒеҲҶдёәдёүзұ»пјҡдёүи§’зҪ‘з”ҹй•ҝз®—жі•гҖҒйҖҗзӮ№жҸ’е…Ҙз®—жі•е’ҢеҲҶжІ»з®—жі•гҖӮдёүи§’зҪ‘з”ҹй•ҝз®—жі•з”ұдәҺеңЁ...
еңЁжҸҗдҫӣзҡ„MATLABжәҗз ҒдёӯпјҢйҮҮз”ЁдәҶpowercrustз®—жі•иҝӣиЎҢзӮ№дә‘зҡ„Delaunayдёүи§’еү–еҲҶгҖӮPowercrustз®—жі•жҳҜдёҖз§ҚеҹәдәҺеҜҶеәҰзҡ„иЎЁйқўйҮҚе»әж–№жі•пјҢе®ғиҖғиҷ‘дәҶзӮ№дә‘зҡ„еҜҶеәҰеҲҶеёғпјҢеҸҜд»ҘеӨ„зҗҶеҷӘеЈ°е’ҢдёҚе®Ңж•ҙзҡ„ж•°жҚ®гҖӮиҜҘз®—жі•йҰ–е…Ҳжһ„е»әдёҖдёӘеҲқжӯҘзҡ„дёүи§’зҪ‘ж јпјҢ...
Delaunayдёүи§’еү–еҲҶеңЁеҸҜи§ҶеҢ–пјҢGISпјҢи®Ўз®—жңәеӣҫеҪўеӯҰдёӯжңүзқҖе№ҝжіӣзҡ„еә”з”ЁгҖӮжң¬ж–Үдё»иҰҒжҳҜй’ҲеҜ№3dдёүи§’зҪ‘еү–еҲҶз®—жі•зҡ„д»Ӣз»ҚпјҢз ”з©¶дёҺеә”з”ЁгҖӮ
еңЁжң¬еҺӢзј©еҢ…дёӯпјҢжҸҗдҫӣзҡ„жҳҜз”ЁMatlabе®һзҺ°зҡ„Delaunayдёүи§’еү–еҲҶз®—жі•гҖӮ `DT1.m`е’Ң`DT2.m`жҳҜдёӨдёӘдё»иҰҒзҡ„Matlabи„ҡжң¬ж–Ү件пјҢе®ғ们еҸҜиғҪеҢ…еҗ«дәҶе®һзҺ°Delaunayдёүи§’еү–еҲҶзҡ„ж ёеҝғз®—жі•гҖӮйҖҡеёёпјҢDelaunayдёүи§’еү–еҲҶзҡ„е®һзҺ°дјҡеҹәдәҺжҹҗз§Қж•°жҚ®з»“жһ„пјҲеҰӮ...
еңЁVBпјҲVisual Basicпјүдёӯе®һзҺ°Delaunayдёүи§’еү–еҲҶпјҢйҖҡеёёж¶үеҸҠеҲ°зј–зЁӢжҠҖе·§е’ҢеҮ дҪ•з®—жі•зҡ„з»“еҗҲгҖӮд»ҘдёӢжҳҜе…ідәҺиҝҷдёӘдё»йўҳзҡ„иҜҰз»Ҷи§ЈйҮҠпјҡ дёҖгҖҒDelaunayдёүи§’еү–еҲҶзҡ„еҹәзЎҖжҰӮеҝө Delaunayдёүи§’еү–еҲҶжҳҜз”ұж•°еӯҰ家BenoГ®t B. MandelbrotжҸҗеҮәзҡ„пјҢе…¶...
еңЁи®Ўз®—жңәеӣҫеҪўеӯҰе’Ңи®Ўз®—еҮ дҪ•йўҶеҹҹпјҢDelaunayдёүи§’еү–еҲҶжҳҜдёҖз§ҚйҮҚиҰҒзҡ„з®—жі•пјҢе®ғе°ҶдёҖдёӘеӨҡиҫ№еҪўеҲҶеүІжҲҗдёҖзі»еҲ—дә’дёҚзӣёдәӨзҡ„дёүи§’еҪўпјҢдҪҝеҫ—жІЎжңүдёҖдёӘдёүи§’еҪўзҡ„йЎ¶зӮ№дҪҚдәҺе…¶д»»дҪ•йӮ»еұ…зҡ„еҶ…еҲҮеңҶдёӯгҖӮиҝҷзҜҮи®Ўз®—еҮ дҪ•дҪңдёҡзҡ„йҮҚзӮ№жҳҜдҪҝз”ЁVC++пјҲVisual ...
йҖҡиҝҮз»“еҗҲDelaunayдёүи§’еү–еҲҶз®—жі•дёҺOpenGLеӣҫеҪўжёІжҹ“жҠҖжңҜпјҢеҸҜд»Ҙжңүж•Ҳең°е°Ҷдёүз»ҙж•Јд№ұзӮ№йӣҶеҸҜи§ҶеҢ–пјҢиҝҷеҜ№дәҺзҗҶи§Је’ҢеҲҶжһҗеӨҚжқӮзҡ„ж•°жҚ®йӣҶйқһеёёжңүз”ЁгҖӮиҝҷз§ҚжҠҖжңҜдёҚд»…еңЁи®Ўз®—жңәиҫ…еҠ©и®ҫи®Ў(CAD)йўҶеҹҹжңүе№ҝжіӣеә”з”ЁпјҢиҝҳеңЁең°иҙЁеӯҰгҖҒеҢ»еӯҰеҪұеғҸеҲҶжһҗзӯүйўҶеҹҹ...
жүҫдәҶеҚҠеӨ©еӣҪеҶ…зҪ‘з«ҷдёҠйғҪжІЎжүҫеҲ°еҘҪз”Ёзҡ„пјҢеҘҪдёҚе®№жҳ“д»ҺеӣҪеӨ–зҡ„зҪ‘з«ҷдёҠдёӢиҪҪеҲ°зҡ„..еёҰзӨәдҫӢж•°жҚ®е’Ңжәҗз Ғ delaunayдёүи§’еү–еҲҶ
4. **ж ёеҝғз®—жі•**пјҡDelaunayдёүи§’еү–еҲҶзҡ„з®—жі•еҸҜд»Ҙжңүи®ёеӨҡе®һзҺ°ж–№ејҸпјҢеҰӮGabrielз®—жі•гҖҒFlipз®—жі•гҖҒ Incrementalж–№жі•жҲ–иҖ…Constrained Delaunay Triangulation (CDT)гҖӮиҝҷдәӣз®—жі•ж №жҚ®зӮ№йӣҶзҡ„зү№зӮ№е’ҢжҖ§иғҪйңҖжұӮжңүжүҖдёҚеҗҢпјҢдҪҶйғҪиҮҙеҠӣдәҺ...
еңЁи®Ўз®—жңә科еӯҰйўҶеҹҹпјҢзү№еҲ«жҳҜеӣҫеҪўеӯҰе’ҢеҮ дҪ•и®Ўз®—дёӯпјҢDelaunayдёүи§’еү–еҲҶжҳҜдёҖз§ҚйҮҚиҰҒзҡ„з®—жі•пјҢз”ЁдәҺе°ҶдёҖз»„зҰ»ж•Јзҡ„зӮ№йӣҶиҪ¬еҢ–дёәдёҖдёӘж— з©ҝеҲәзҡ„дёүи§’зҪ‘ж јпјҢдҪҝеҫ—жҜҸдёӘзӮ№йғҪиў«е…¶еҢ…еӣҙзҡ„дёүи§’еҪўзҡ„еҶ…еҲҮеңҶеҚҠеҫ„жңҖеӨ§гҖӮеңЁPythonзј–зЁӢзҺҜеўғдёӯпјҢе®һзҺ°...
гҖҠйҷҗе®ҡDelaunayдёүи§’зҪ‘ж јеү–еҲҶжҠҖжңҜ-жқЁй’ҰгҖӢдёҖд№Ұж·ұе…ҘжҺўи®ЁдәҶзҪ‘ж јеү–еҲҶз®—жі•зҡ„ж ёеҝғеҶ…е®№пјҢзү№еҲ«жҳҜеңЁдәҢз»ҙе№ійқўе’Ңдёүз»ҙз©әй—ҙдёӯзҡ„йҷҗе®ҡDelaunayдёүи§’еү–еҲҶжҠҖжңҜгҖӮDelaunayдёүи§’еү–еҲҶжҳҜдёҖз§ҚеңЁеҮ дҪ•и®Ўз®—гҖҒи®Ўз®—жңәеӣҫеҪўеӯҰгҖҒж•°еҖјжЁЎжӢҹзӯүйўҶеҹҹе№ҝжіӣ...
Delaunayдёүи§’еү–еҲҶжҳҜдёҖз§ҚеңЁеҮ дҪ•и®Ўз®—йўҶеҹҹе№ҝжіӣдҪҝз”Ёзҡ„з®—жі•пјҢе®ғйҖҡиҝҮе°ҶзӮ№йӣҶеҲҶеүІжҲҗдёҖзі»еҲ—дә’дёҚзӣёдәӨзҡ„дёүи§’еҪўпјҢдҪҝеҫ—жҜҸдёӘдёүи§’еҪўзҡ„еҶ…еҲҮеңҶеҶ…жІЎжңүе…¶д»–иҫ“е…ҘзӮ№гҖӮиҝҷз§Қеү–еҲҶж–№жі•еңЁи®Ўз®—жңәеӣҫеҪўеӯҰгҖҒең°зҗҶдҝЎжҒҜзі»з»ҹгҖҒжңүйҷҗе…ғеҲҶжһҗгҖҒж•°жҚ®еҸҜи§ҶеҢ–зӯү...
delaunayдёүи§’еү–еҲҶжҳҜдёҖз§ҚеңЁдәҢз»ҙз©әй—ҙдёӯз»„з»ҮзӮ№йӣҶзҡ„ж–№жі•пјҢйҖҡиҝҮе°ҶзӮ№иҝһжҺҘжҲҗдёҖзі»еҲ—дә’дёҚзӣёдәӨзҡ„дёүи§’еҪўпјҢеҪўжҲҗдёҖдёӘе®Ңж•ҙзҡ„иҰҶзӣ–гҖӮиҝҷдёӘиҝҮзЁӢеңЁи®Ўз®—жңәеӣҫеҪўеӯҰгҖҒең°зҗҶдҝЎжҒҜзі»з»ҹгҖҒ科еӯҰи®Ўз®—еҸҜи§ҶеҢ–зӯүйўҶеҹҹжңүзқҖе№ҝжіӣзҡ„еә”з”ЁгҖӮеңЁOpenCVеә“дёӯпјҢ...
жң¬ж–ҮеңЁиҜҰз»Ҷз ”з©¶е’ҢеҲҶжһҗдәҶе…ёеһӢзҡ„Delaunayдёүи§’еү–еҲҶз®—жі•зҡ„жҖқжғіеҗҺпјҢй’ҲеҜ№еўһйҮҸ з®—жі•дёӯзҡ„е…ій”®й—®йўҳжҸҗеҮәж”№иҝӣзҡ„ж–№жі•пјҢд»ҺйҷҚдҪҺз®—жі•зҡ„ж—¶й—ҙеӨҚжқӮеәҰзҡ„и§’еәҰеҮәеҸ‘пјҢд»ҘзӮ№ е®ҡдҪҚжҗңзҙўиҝҷдёҖе…ій”®й—®йўҳдёәеҲҮе…ҘзӮ№пјҢжҸҗеҮәж–°зҡ„ж”№иҝӣжҗңзҙўзҡ„ж–№жі•пјҢиҜҘз®—жі•...
жҖ»зҡ„жқҘиҜҙпјҢDelaunayдёүи§’еү–еҲҶз®—жі•еңЁдёүз»ҙз©әй—ҙдёӯзҡ„еә”з”ЁжҳҜдёҖйЎ№еӨҚжқӮдҪҶйҮҚиҰҒзҡ„д»»еҠЎпјҢе®ғдҫқиө–дәҺзІҫеҝғи®ҫи®Ўзҡ„ж•°жҚ®з»“жһ„е’Ңй«ҳж•Ҳзҡ„з®—жі•гҖӮCиҜӯиЁҖз”ұдәҺе…¶еә•еұӮжҺ§еҲ¶е’ҢжҖ§иғҪдјҳеҠҝпјҢеёёиў«з”ЁжқҘе®һзҺ°иҝҷзұ»и®Ўз®—еҜҶйӣҶеһӢзҡ„д»»еҠЎгҖӮйҖҡиҝҮдҪҝз”ЁеҰӮtetgenиҝҷж ·зҡ„...