模式分类笔记 -- 共轭梯度下降(1)

在看人工神经网络的时候，经常有些书提及一些提高或改善网络学习效率的方法。这里面包括很多，有很多从其它学科借鉴过来的想法，知识。其中，共轭梯度下降法就是一个比较常见，它属于二阶技术，也经常被用到无约束优化的情形下。

 

在神经网络的书中，这个方法总是被赋予很少的笔墨，但过于简短的描述常带来更多的疑惑。起码我没有那么多书去查阅，记下点什么是个更好的选择，一是从中能读到很有启发的产生过程，二是弥补这慢慢记忆衰退的大脑。（每天脑袋里有那么多东西跑来跑去，过目不忘，算了吧）

 

我这篇内容主要来自：An Introduction to the Conjugate Gradient Method Without the Agonizing Pain ， 很容易搜到，因为很多地方引用。原文的笔者是因为各个教科书（不管是什么地方啦）对此方法阐述的含含糊糊不满意，遂萌生了自己要把它解释清楚的强烈冲动，呵呵。

 

先阐明下应用场景：它解决的是优化问题，理念很简单，从二次型优化出发。

二次型优化有时候不是很明显有谷底嘛（以此种为例），解一下方程不就成了。但共轭梯度下降法作为一种迭代方法，而不是直接求解，当然是因为矩阵计算比较费劲，比较耗内存。但共轭梯度下降适合的是稀疏矩阵 ，毕竟它需要迭代好几步的，如果矩阵比较稠密，最好的方式，你还是因式分解系数矩阵去计算吧，用不上这种逼近算法了，处理矩阵的时间可能和迭代的时间差别不大，且分解完后，求解相当方便。

 

给一个二次型形式: f(x) = 1/2 x'Ax - b'x + c， f'(x) = 1/2 A'x + 1/2Ax + b

A是矩阵，b是向量。当A是正定对阵矩阵的时候，f(x)在当A(x)=b的时候被最小化。其实A不对阵也无所谓，因为1/2(A' + A)，这个可是对称的。

 

为什么正定对称矩阵有如此好的性质，讨论的时候中意它，负定，奇异非正定等都有不同的图形表象 ？考虑任意点p，以及最优点x=A''b(这里仍然用''表示逆矩阵)。

f(p) = f(x) + 1/2(p-x)'A(p-x),当p!=x时，很显然f(p) = f(x).

 

一个点下降最快的方向 -f'(xi) = b - Axi ， 我们以ei = xi - x ，来标记我们离最终想要结果间的偏差。那么ri = b - Axi就标记我们离正确的b有多远，很容易注意到 ri = -f'(xi) = -Aei 。每一次看到r记号 ，记得它等同梯度 就行了。

 

假设我们从x0点开始，我们沿着梯度下降的方向走，那么需要找到下一个点x1 = x0 + ar(0) . 那么问题来了，每一次我们应该迈多大步，也就是要求那个a，这里a在一些式子里的名字叫做学习率 。

 

------

上面一直说的是最速下降，结合图来说一下，上了一张大图，好像是模式分类里自己贴的最大图了。当我们寻找梯度方向的时候，梯度的方向首先是垂直于(a)图的等高线的，(b)图的二次型才是真是的函数图像。

 

最开始看的时候，我脑袋里面一直认为最速下降方向是往最低点的方向指。直到自己在文章的引导表述里觉得有些说不通，无奈亲手代入点解了下结果，才发现自己错了，梯度的方向是如(a)图里的实线方向，平行于x1，x2平面的。(a)图一直认为最简单，都没在意，教训啊。况且对x的求导得出的结果就是关于x1，x2的一次的， 肯定是平行于坐标平面，说简单点就是解出来的f'(x)就是平面上一点。

 

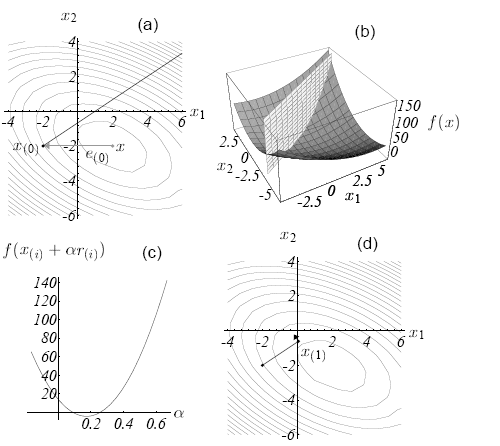
(b)图里的平面和抛物面的交线是个抛物线，梯度下降的候选点就在这条抛物线上。到哪个点最低，好像大家在(c)图上一眼就看的出来，但程序不知道啊，会试图在这条抛物线上（也等同于就是在梯度下降的那条实线上）做搜索。当上面的学习率式子对a求导的时候，会得到

 

d(f(x1))/da = f'(x1)'r(0) 。

 

这个结果一出，自然而然，与上一个点的梯度方向垂直的点是最速下降的。这个点自然是抛物线上的最低点的，不用怀疑。

 

 

直接引用结果了哈， a = r(0)'r(0)/r(0)'Ar(0)

 

在最速下降这一块，得到的式子也就是这个 x(i+1) = x(i) + a(i)r(i)

 

如果两边都乘以-A，再加上b，那么上式就变成下式

r(i+1) = r(i) - a(i)Ar(i)

 

这样有什么好处呢，因为变换前的式子的最速下降算法的最大开销在于每次的矩阵乘法运算 ，包括两次，一次求r(i),一次求a(i), 变换后的话就可以只有一次矩阵乘法[Ar(i)]就可以了，保存起来第二次调用直接用。当然r(0)那一次矩阵运算还是免不掉的。

 

一点点最速下降也写了这么多文字，不过还是记详细点好。自己作为寥寥的几个看官，再次回到这页面的时候若想追究些细节还有迹可循。

 

文章分几节来写比较好，所以分割此篇作为（1）。

 

还是会往共轭下降方向走，下面会从特征向量方向切入。